Modulo 3

Módulo 3
Trigonometria, Logaritmos e Exponencial
Trigonometria
As funções trigonométricas diretas são também conhecidas como função
circulares. As funções trigonométricas diretas são o cosseno, seno, tangente entre
outras.
C
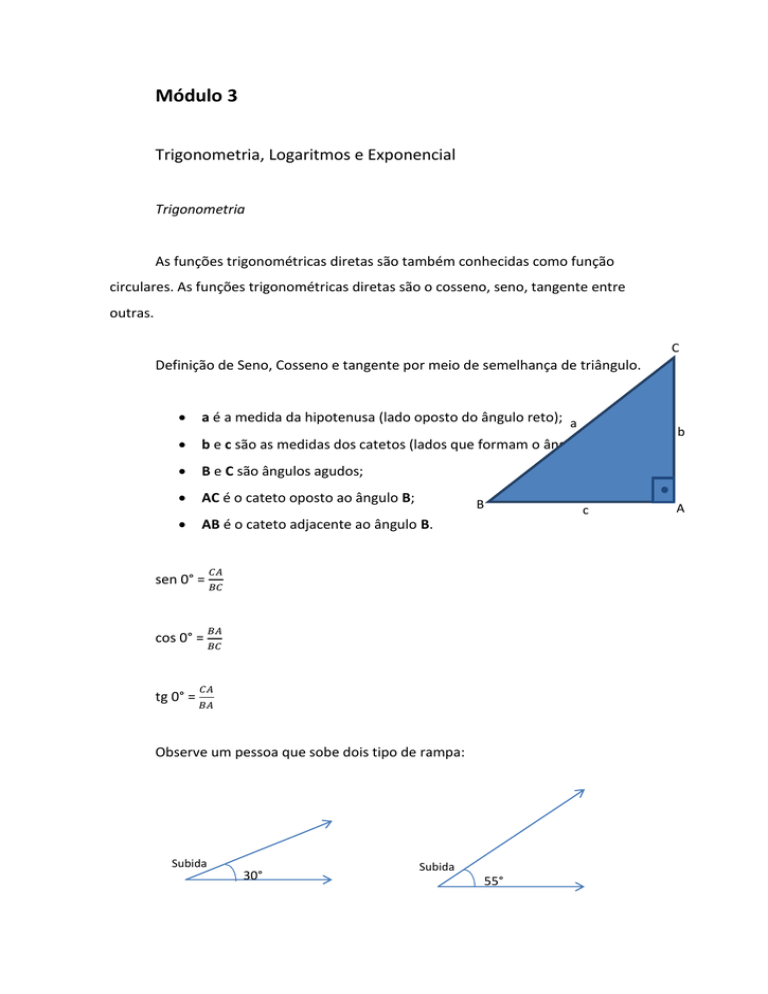
Definição de Seno, Cosseno e tangente por meio de semelhança de triângulo.

a é a medida da hipotenusa (lado oposto do ângulo reto); a

b e c são as medidas dos catetos (lados que formam o ângulo reto);

B e C são ângulos agudos;

AC é o cateto oposto ao ângulo B;

AB é o cateto adjacente ao ângulo B.
B
sen 0° =
cos 0° =
tg 0° =
Observe um pessoa que sobe dois tipo de rampa:
Subida
30°
Subida
55°
c
b
A
Dizemos que a segunda rampa é mais íngreme ou tem aclive maior, pois seu
ângulo de subida é maior (55° > 30º).
Tangente
Usaremos a palavra tangente para associar a medida do ângulo de subida e o
índice na mesma subida. A tangente do ângulo de subida é igual ao índice de subida
associado, ele sera indicada por
.
α
Altura
Afastamento
Tangente de um ângulo de subida =
Tg α =
Tg α =
= índice de subida
Seno
Em qualquer subida podemos determinar a razão entre a altura e o percurso,
que será um número indicado por
, ao qual chamaremos de seno do ângulo.
= número
Percurso
α
Seno de um ângulo de subida =
sen α =
sen α =
Altura
Cosseno
Em qualquer subida podemos determinar a razão entre o afastamento e o
percurso, número que indicaremos por
, ao qual chamaremos de cosseno do ângulo.
= número
Percurso
Altura
α
Afastamento
Cosseno de um ângulo de subida =
cos α =
cos α =
Relações entre seno, cosseno e tangente
A razões trigonométricas seno, cosseno e tangente se relacionam de varias
formas, como veremos a seguir:
Relação fundamental do triângulo retângulo
Logaritmos
A função logarítmica é definida como:
Forma logarítmica
a: base da potência
b: logaritmando
c: logaritmo
Propriedades operatórias do logaritmos
1ª Logaritmo de um produto
O logaritmo de um produto é igual à soma dos logaritmos dos fatores tomados
na mesma base, isto é:
com a > 0, c > 0 e 1 ≠ b > 0.
2ª Logaritmo de um quociente
O logaritmo de um quociente é igual ao logaritmo do numerador menos o
logaritmo do denominador tomados mesma base, isto é:
com a > 0, c > 0 e 1 ≠ b > 0.
3ª Logaritmo de uma potência
O logaritmo de uma potência é igual ao produto do expoente pelo logarimo da
base da potência, isto é:
com a > 0 e 1 ≠ b > 0.
Exponencial
A função exponencial é definida como:
Expoente inteiro positivo: Se α é um número real denominado de base e
inteiro e positivo denominado expoente, a expressão
é
representa o produto de
fatores, todos iguais a α, ou seja:
fatores
Expoente inteiro negativo: Sendo α um número real não nulo (α ≠ 0) e
um
número inteiro negativo, define:
Expoente racional fracionário: Sendo α um número real positivo (α≠0) e
número inteiro e positivo, define-se:
e
Expoente Zero: convenciona-se que
, com α≠0
Propriedades Gerais
Se
e
são números reais, valem as seguintes propriedades:
Propriedade
Regra
Repete-se a base e somam-se os expoentes.
Repete-se a base e subtraem-se os expoentes.
Repete-se a base e multiplicam-se os expoentes.
Eleva-se cada fator ao expoente comum.
Eleva-se o numerador e o denominador ao expoente
comum.
(com
≠ 0)