Enviado por
common.user14149
formulas trigonometricas

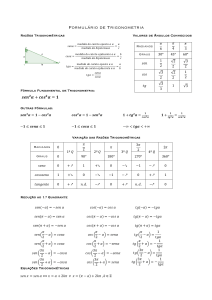
Formulário de Trigonometria Razões Trigonométricas Valores de Ângulos Conhecidos 𝑠𝑒𝑛𝛼 = 𝑐𝑜𝑠𝛼 = 𝑚𝑒𝑑𝑖𝑑𝑎 𝑑𝑜 𝑐𝑎𝑡𝑒𝑡𝑜 𝑜𝑝𝑜𝑠𝑡𝑜 𝑎 𝛼 𝑎 = 𝑚𝑒𝑑𝑖𝑑𝑎 𝑑𝑎 ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 𝑐 𝑚𝑒𝑑𝑖𝑑𝑎 𝑑𝑜 𝑐𝑎𝑡𝑒𝑡𝑜 𝑎𝑗𝑑𝑎𝑐𝑒𝑛𝑡𝑒 𝑎 𝛼 𝑏 = 𝑚𝑒𝑑𝑖𝑑𝑎 𝑑𝑎 ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎 𝑐 Radianos 𝜋 6 𝜋 4 𝜋 3 Graus 30° 45° 60° 𝑠𝑒𝑛 1 2 √2 2 √3 2 𝑐𝑜𝑠 √3 2 √2 2 1 2 𝑡𝑔 √3 3 1 √3 𝑚𝑒𝑑𝑖𝑑𝑎 𝑑𝑜 𝑐𝑎𝑡𝑒𝑡𝑜 𝑜𝑝𝑜𝑠𝑡𝑜 𝑎 𝛼 𝑎 𝑡𝑔𝛼 = = 𝑚𝑒𝑑𝑖𝑑𝑎 𝑑𝑜 𝑐𝑎𝑡𝑒𝑡𝑜 𝑎𝑗𝑑𝑎𝑐𝑒𝑛𝑡𝑒 𝑎 𝛼 𝑏 𝑡𝑔𝛼 = 𝑠𝑒𝑛𝛼 𝑐𝑜𝑠𝛼 Fórmula Fundamental de Trigonometria: 𝒔𝒆𝒏𝟐 𝜶 + 𝒄𝒐𝒔𝟐 𝜶 = 𝟏 Outras Fórmulas: 𝟏 𝟏 𝒔𝒆𝒏𝟐 𝜶 = 𝟏 − 𝒄𝒐𝒔𝟐 𝜶 𝒄𝒐𝒔𝟐 𝜶 = 𝟏 − 𝒔𝒆𝒏𝟐 𝜶 𝟏 + 𝒕𝒈𝟐 𝜶 = 𝒄𝒐𝒔𝟐𝜶 −𝟏 ≤ 𝒔𝒆𝒏𝜶 ≤ 𝟏 −𝟏 ≤ 𝒄𝒐𝒔𝜶 ≤ 𝟏 −∞ < 𝒕𝒈𝜶 < +∞ Variação das Razões Trigonométricas Radianos 0 1º 𝑄 𝜋 2 𝜋 2º 𝑄 90° 3º 𝑄 180° 3𝜋 2 2𝜋 4º 𝑄 Graus 0 𝑠𝑒𝑛𝑜 0 +↗ 1 +↘ 0 −↘ −1 −↗ 0 𝑐𝑜𝑠𝑠𝑠𝑒𝑛𝑜 1 +↘ 0 −↘ −1 −↗ 0 +↗ 1 𝑡𝑎𝑛𝑔𝑒𝑛𝑡𝑒 0 +↗ 𝑛. 𝑑. −↗ 0 +↗ 𝑛. 𝑑. −↗ 0 270° 360° Redução ao 1.º Quadrante 𝑠𝑒𝑛(−𝛼) = −𝑠𝑒𝑛 𝛼 𝑐𝑜𝑠(−𝛼) = 𝑐𝑜𝑠 𝛼 𝑡𝑔(−𝛼) = −𝑡𝑔𝛼 𝑠𝑒𝑛(𝜋 − 𝛼) = 𝑠𝑒𝑛 𝛼 𝑐𝑜𝑠(𝜋 − 𝛼) = −𝑐𝑜𝑠 𝛼 𝑡𝑔(𝜋 − 𝛼) = −𝑡𝑔𝛼 𝑠𝑒𝑛(𝜋 + 𝛼) = −𝑠𝑒𝑛 𝛼 𝑐𝑜𝑠(𝜋 + 𝛼) = −𝑐𝑜𝑠 𝛼 𝑡𝑔(𝜋 + 𝛼) = 𝑡𝑔𝛼 𝜋 𝑐𝑜𝑠 M − 𝛼N = 𝑠𝑒𝑛𝛼 2 𝜋 𝑐𝑜𝑠 M + 𝛼N = −𝑠𝑒𝑛𝛼 2 3𝜋 𝑐𝑜𝑠 O − 𝛼P = −𝑠𝑒𝑛𝛼 2 3𝜋 𝑐𝑜𝑠 O + 𝛼P = 𝑠𝑒𝑛𝛼 2 𝜋 1 𝑡𝑔 M − 𝛼N = 2 𝑡𝑔𝛼 𝜋 1 𝑡𝑔 M + 𝛼N = − 2 𝑡𝑔𝛼 3𝜋 1 𝑡𝑔 O − 𝛼P = 2 𝑡𝑔𝛼 3𝜋 1 𝑡𝑔 O + 𝛼P = − 2 𝑡𝑔𝛼 𝜋 𝑠𝑒𝑛 M − 𝛼N = 𝑐𝑜𝑠𝛼 2 𝜋 𝑠𝑒𝑛 M + 𝛼N = 𝑐𝑜𝑠𝛼 2 3𝜋 𝑠𝑒𝑛 O − 𝛼P = −𝑐𝑜𝑠𝛼 2 3𝜋 𝑠𝑒𝑛 O + 𝛼P = −𝑐𝑜𝑠𝛼 2 Equações Trigonométricas 𝑠𝑒𝑛 𝑥 = 𝑠𝑒𝑛 𝛼 ⟺ 𝑥 = 𝛼 + 2𝑘𝜋 ∨ 𝑥 = (𝜋 − 𝛼) + 2𝑘𝜋 , 𝑘 ∈ ℤ 𝟏 𝟏 + 𝒕𝒈𝟐𝜶 = 𝒔𝒆𝒏𝟐𝜶 𝑐𝑜𝑠 𝑥 = 𝑠𝑒𝑛 𝛼 ⟺ 𝑥 = 𝛼 + 2𝑘𝜋 ∨ 𝑥 = −𝛼 + 2𝑘𝜋 , 𝑘 ∈ ℤ 𝑡𝑔 𝑥 = 𝑡𝑔𝛼 ⟺ 𝑥 = 𝛼 + 𝑘𝜋 , 𝑘 ∈ ℤ Funções trigonométricas Funções 𝒙 ⟶ 𝒔𝒆𝒏 𝒙 𝒙 ⟶ 𝒄𝒐𝒔 𝒙 Domínio ℝ ℝ Contradomínio [−1,1] [−1,1] Zeros 𝑥 = 𝑘𝜋, 𝑘 ∈ ℤ Variação de sinal Período monotonia 𝒙 ⟶ 𝒕𝒈 𝒙 𝜋 ,𝑥 ∈ ℝ𝑥 ≠ + 𝑘𝜋, 𝑘 ∈ ℤ6 2 ℝ Positivo: 1.º Q e 2.º Q 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ 2 Positivo: 1.º Q e 4.º Q Positivo: 1.º Q e 3.º Q Negativo: 3.ºQ e 4.º Q Negativo: 2.ºQ e 4.º Q Negativo: 2.ºQ e 4.º Q 2𝜋 𝑠𝑒𝑛(𝑥 + 2𝜋) = 𝑠𝑒𝑛 𝑥 𝑥= 2𝜋 cos(𝑥 + 2𝜋) = 𝑐𝑜𝑠 𝑥 𝑥 = 𝑘𝜋, 𝑘 ∈ ℤ 𝜋 𝑡𝑔(𝑥 + 𝜋) = 𝑡𝑔 𝑥 Crescente: 1.º Q e 4.º Q Crescente: 3.º Q e 4.º Q Crescente em todos os Decrescente: 2.º Q e 3.º Q Decrescente: 1.º Q e 2.º Q quadrantes ! Máximo: 1 para 𝑥 = " + 2𝑘𝜋, 𝑘 ∈ ℤ Máximo: 1 para 𝑥 = 2𝑘𝜋, 𝑘 ∈ ℤ Mínimo:−1 para 𝑥 = 𝑘𝜋, 𝑘 ∈ ℤ Mínimo:−1 para 𝑥 = 𝜋 + 2𝑘𝜋, 𝑘 ∈ ℤ Paridade Função Ímpar: 𝑠𝑒𝑛(−𝑥) = −𝑠𝑒𝑛 𝑥 Função Par: 𝑐𝑜𝑠(−𝑥) = 𝑐𝑜𝑠 𝑥 Função Ímpar: 𝑡𝑔(−𝑥) = −𝑡𝑔 𝑥 Assíntotas não tem não tem verticais: 𝑥 = " + 𝑘𝜋, 𝑘 ∈ ℤ Extremos Não tem !