Enviado por
common.user7733
complemento de plano inclinado
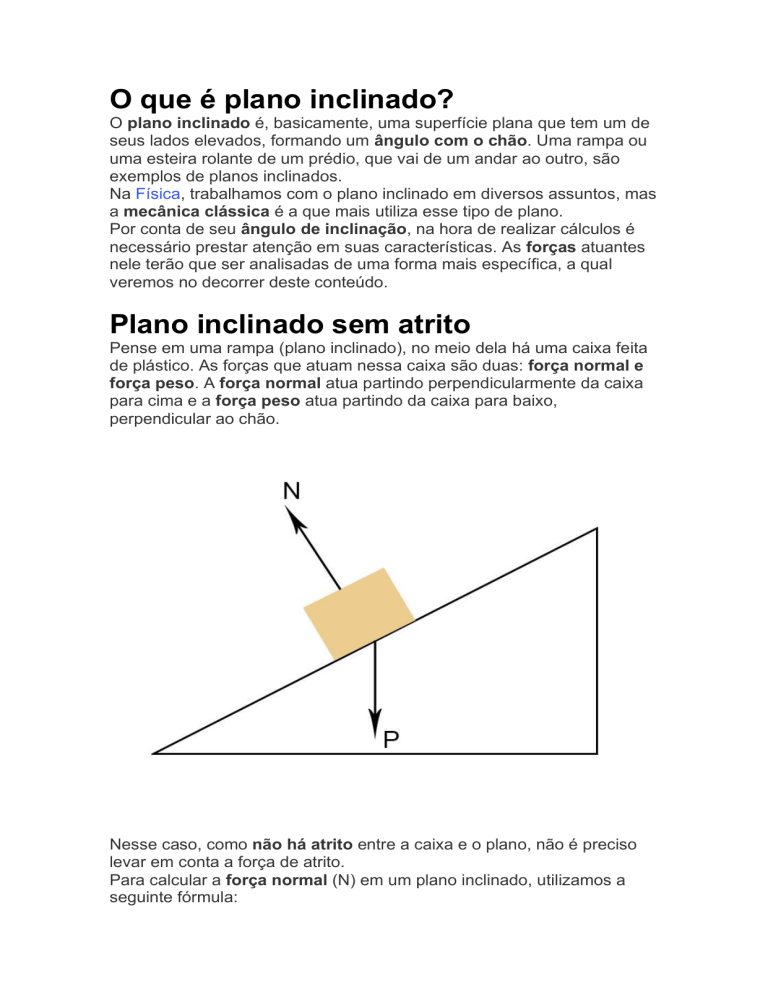
O que é plano inclinado? O plano inclinado é, basicamente, uma superfície plana que tem um de seus lados elevados, formando um ângulo com o chão. Uma rampa ou uma esteira rolante de um prédio, que vai de um andar ao outro, são exemplos de planos inclinados. Na Física, trabalhamos com o plano inclinado em diversos assuntos, mas a mecânica clássica é a que mais utiliza esse tipo de plano. Por conta de seu ângulo de inclinação, na hora de realizar cálculos é necessário prestar atenção em suas características. As forças atuantes nele terão que ser analisadas de uma forma mais específica, a qual veremos no decorrer deste conteúdo. Plano inclinado sem atrito Pense em uma rampa (plano inclinado), no meio dela há uma caixa feita de plástico. As forças que atuam nessa caixa são duas: força normal e força peso. A força normal atua partindo perpendicularmente da caixa para cima e a força peso atua partindo da caixa para baixo, perpendicular ao chão. Nesse caso, como não há atrito entre a caixa e o plano, não é preciso levar em conta a força de atrito. Para calcular a força normal (N) em um plano inclinado, utilizamos a seguinte fórmula: • • • • • • • • N = m . g . cos θ Em que: N é a força normal (N); m é a massa (Kg); g é a aceleração da gravidade (m/s²); cos θ é o ângulo de inclinação. Para calcular a força peso (P) em um plano inclinado, utilizamos a seguinte fórmula: P = m . g . cos θ Em que: P é a força peso (N); m é a massa (Kg); g é a aceleração da gravidade (m/s²); cos θ é o ângulo de inclinação. Como se pode perceber, é preciso levar em consideração o ângulo de inclinação, pois isso influencia em algumas questões, como a quantidade de força necessária para mover para cima a caixa ou para segurá-la sem escorregar. Plano inclinado com atrito • • • Imagine o mesmo exemplo anterior, só que agora a caixa é de madeira e há atrito entre ela e o chão. A força peso e normal continuam atuando da mesma forma. Porém, além delas, entra em cena a força de atrito, que atua no sentido contrário ao do movimento. Para calcular o atrito, utilizamos a seguinte fórmula: Fat = μ . N Em que: Fat é a força de atrito (N); μ é o coeficiente de atrito; N é a força normal (N). O coeficiente de atrito (μ) não tem unidade de medida, porque ele é adimensional, ou seja, um número puro sem medida. O valor dele depende de cada tipo de material, sendo que alguns possuem atrito maior e outros atrito menor. Um exemplo de plano inclinado com atrito no cotidiano está na pista de skate ou roller. Aceleração no plano inclinado • • Como o plano está inclinado, vai haver aceleração constante, devido à ação da força normal e força peso. Porém, para calcular essa aceleração, é preciso utilizar a decomposição de vetores. Isso porque a força peso que é utilizada para encontrar a aceleração não está perpendicular à caixa, mas ao chão no qual está o plano inclinado. Dessa forma, é preciso decompor os vetores em dois (x e y) para encontrarmos a força que atua na mesma direção do movimento que a caixa realiza sobre o plano. Assim, temos: Px = P . sen θ (paralelo ao plano); Py = P . cos θ (perpendicular ao plano). De acordo com a Segunda Lei de Newton, temos que: F=m.a Sendo assim: Px = m . a P . sen θ = m . a m . g . sen θ = m . a a = g . sen θ É importante ressaltar que, nesse caso, estamos trabalhando com um plano inclinado sem atrito. Portanto, podemos perceber é que a aceleração não depende da massa do objeto que está sobre o plano. Ela só depende da inclinação e da aceleração da gravidade. Dessa forma, quanto mais inclinado estiver o plano, maior vai ser a aceleração. Porém, em um plano inclinado com atrito, é preciso considerar a força. Forças no plano inclinado • • • Como já foi citado, há algumas forças que atuam em um objeto que está sobre um plano inclinado. Entre elas, temos: força normal (N); força peso (P); força de atrito (Fat). Em algumas delas, será necessário aplicar a decomposição de vetores, como é o caso da força peso, quando se quer encontrar a aceleração. Abaixo, temos uma imagem de todas elas atuando em um objeto sobre um plano inclinado: Plano inclinado fórmulas • Aqui, seguem as fórmulas utilizadas em um plano inclinado: força normal: N = m . g . cos θ; • força peso: P = m . g . cos θ; força de atrito: Fat = μ . N; • aceleração: a = g . sen θ. • Leis de Newton plano inclinado Como comentado no início do texto, a mecânica clássica é a que mais faz uso do plano inclinado, principalmente quando se trata das leis de Newton. Por isso, vamos ver um pouco sobre as aplicações das leis de Newton no plano inclinado. Primeiramente, são três as leis de Newton: LEI DA INÉRCIA: TODO OBJETO PERMANECE EM SEU ESTADO DE REPOUSO OU DE MOVIMENTO UNIFORME EM UMA LINHA RETA, A MENOS QUE SEJA OBRIGADO A MUDAR AQUELE ESTADO POR FORÇAS IMPRIMIDAS SOBRE ELE; SEGUNDA LEI DE NEWTON: A ACELERAÇÃO DE UM OBJETO É DIRETAMENTE PROPORCIONAL À FORÇA RESULTANTE ATUANDO SOBRE ELE; TEM O MESMO SENTIDO QUE ESTA FORÇA E É INVERSAMENTE PROPORCIONAL À MASSA DO OBJETO; LEI DA AÇÃO E REAÇÃO: SEMPRE QUE UM OBJETO EXERCE UMA FORÇA SOBRE UM OUTRO OBJETO, ESTE EXERCE UMA FORÇA IGUAL E OPOSTA SOBRE O PRIMEIRO. Sendo assim, elas estudam as forças que atuam em um corpo, esteja ele em um plano inclinado ou não. Levando em consideração apenas o plano inclinado, as forças que atuam sobre ele nos permitem calcular o atrito, a aceleração do objeto e sua força peso. Aliás, é o que estávamos vendo até agora neste post. Em exemplos práticos do dia a dia, isso pode ser aplicado na construção de esteiras rolantes, sejam elas para ambientes comerciais ou industriais, em rampas e até em escorregador de parques de diversão.









