exercicio final

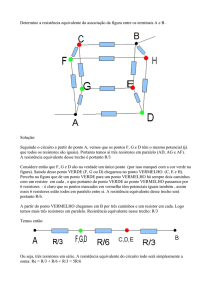
Calcule a resistência equivalente da associação mista de resistores entre os pontos A e B no circuito
abaixo:
Circuito 1
Solução:
Neste exercício existe uma associação mista de resistores pois há associação em paralelo e em série.
Os resistores de 1,2 Ω e 6 Ω estão em paralelo, enquanto que os de 5 Ω e 7 Ω e os de 4 Ω e 8 Ω estão
em série.
A solução deste tipo de exercício deve ser feita passo a passo, calculando as resistências equivalentes
de cada associação, uma por vez e no fim, o resultado será obtido naturalmente.
Cálculo da associação paralela entre os resistores de 1,2 Ω e 6 Ω
O cálculo da resistência equivalente de uma associação em paralelo é obtida usando a seguinte
fórmula:
Onde Req é a resistência equivalente da associação de resistores, R1 neste caso vale 1,2 Ω e R2 vale
6 Ω. Substituindo os valores temos:
Assim, como 1/Req = 1 Ω, então Req = 1 Ω. Logo, a associação de resistores da figura é equivalente
a:
Cálculo da associação em série entre os resistores de 5 Ω e 7 Ω e os de 4 Ω
e8Ω
O cálculo da associação de resistores em série é mais simples pois basta somar as resistências. No
caso, a resistência equivalente da associação em série entre 5 Ω e 7 Ω será 12 Ω e entre 4 Ω e 8 Ω
será 12 Ω também. Assim, o circuito fica:
Cálculo da associação paralela entre os dois resistores de 12 Ω
Veja que as resistência de 12 Ω ficaram em paralelo. Usando a fórmula para o cálculo da Req para
associação em paralelo temos:
Assim, como 1/Req = 1/6, então Req = 6 Ω.
Cálculo da resistência equivalente de todo o circuito
Após o último cálculo, temos que o circuito fica:
As duas resistências restantes estão em série, logo a Resistência Equivalente do circuito será de 7 Ω.
Circuito 2
Solução:
O resistor de 2Ω entre os pontos D e F e o resistor de 4Ω entre os pontos F e E estão em série e
podem ser somados, ficando:
As duas resistências de 6Ω entre os pontos D e E estão em paralelo. Utilizando a regra da
assossiação de resistores em paralelo, o circuito fica:
Como é possível observar, os resistores de 3Ω entre os pontos D e E e os pontos E e C estão em
série. Somando-os temos um resistor de 6Ω, como pode ser visto a seguir:
Observa-se que os resistores de 6Ω estão em paralelo. Calculando-os temos:
Seguindo o mesmo raciocínio, percebe-se que os resistores de 3Ω estão em série, resultando num
resistor de 6Ω, que estará em paralelo com o resistor de 6Ω já existente.
Calculando a resistência equivalente da associação em paralelo dos resistores de 6Ω, temos:
Assim, ficam restando apenas duas resistências em série, uma de 1Ω e outra de 3Ω. Somando-as,
temos a resistência equivalente entre os pontos A e B = 4Ω.
Calcule a resistência equivalente da associação mista de resistores entre os pontos A e B no circuito
abaixo:
Circuito 4
Solução:
Utilizando a estratégia de unir pontos ligados por um curto, pode-se perceber que as resistências de
80Ω estão em paralelo, tendo como resistência equivalente uma de 40Ω.
Temos, agora, as resistências de 60Ω e de 40Ω em série que, somadas, geram uma resistência
equivalente de 100Ω
ficando as duas resistências de 100Ω em paralelo. Calculando a resistência equivalente temos:
Assim, as resistências de 150Ω e de 50Ω ficam em série. Somadas temos uma resistência
equivalente de 200Ω em paralelo com a outra de 200Ω.
Resolvendo esta associação em paralelo, temos que a resistência equivalente entre os pontos A e B
é de 100Ω.
Calcule a resistência equivalente da associação mista de resistores entre os pontos A e B no circuito
abaixo:
Circuito 5
Solução:
Inicialmente, é importante dar nomes aos pontos:
Verificamos que há um curto entre os pontos C e D. Como já comentado nos outros casos, a melhor
forma de visualizar a disposição dos resistores é unindo os pontos ligados por curto. Neste caso, os
pontos C e D tornam-se um ponto só. Assim, dispomos os pontos no "espaço" e vamos unindo-os
com o que houver entre eles, da seguinte forma:
Entre os pontos A e B há uma resistência;
Entre os pontos A e C há uma resistência;
Entre os ponto A e D há uma resistência;
Entre os pontos C e B há uma resistência;
E, finalmente, entre os pontos D e B há uma resistência;
Agora fica fácil visualizar o circuito, que deve ser resolvido iniciando pelos resistores em paralelo.
Como devemos calcular a resistência equivalente entre A e B, temos que os resistores R/2 estão em
série (neste momento o ponto C//D pode ser eliminado).
Restando dois resistores em paralelo. Assim, a resistência equivalente entre A e B é R/2.