Ficha Avaliação Contínua − Introdução ao Estudo de Funções
Matemática A - 10o Ano
Ficha de Avaliação Contínua - Introdução ao Estudo de Funções
Colectânea de Fichas de Trabalho 10o Ano
Nuno Miguel Guerreiro
• Nas questões desta ficha, apresenta o teu raciocínio de forma clara, indicando todos os cálculos que
tiveres de efetuar e todas as justificações que entenderes necessárias.
• Atenção: Quando para um resultado não é pedida aproximação pretende-se sempre o valor exato.
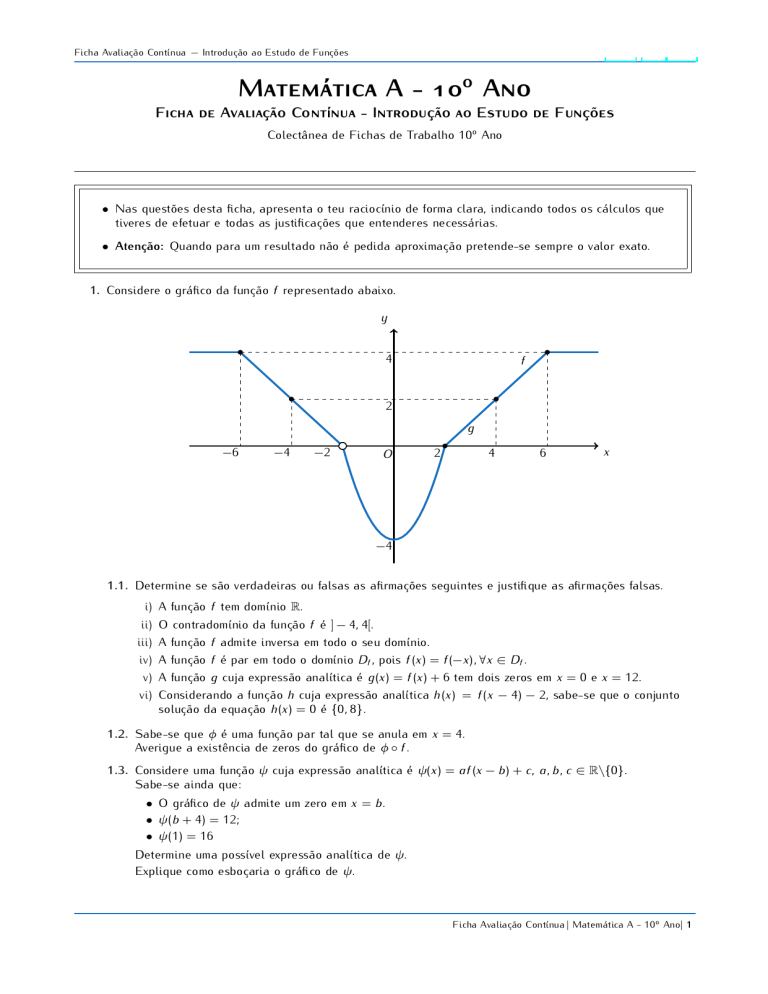
1. Considere o gráfico da função f representado abaixo.
y
4
f
2
g
−6
−4
−2
O
2
4
6
x
−4
1.1. Determine se são verdadeiras ou falsas as afirmações seguintes e justifique as afirmações falsas.
i) A função f tem domínio R.
ii) O contradomínio da função f é ] − 4, 4[.
iii) A função f admite inversa em todo o seu domínio.
iv) A função f é par em todo o domínio Df , pois f(x) = f(−x), ∀x ∈ Df .
v) A função g cuja expressão analítica é g(x) = f(x) + 6 tem dois zeros em x = 0 e x = 12.
vi) Considerando a função h cuja expressão analítica h(x) = f(x − 4) − 2, sabe-se que o conjunto
solução da equação h(x) = 0 é {0, 8}.
1.2. Sabe-se que φ é uma função par tal que se anula em x = 4.
Averigue a existência de zeros do gráfico de φ ◦ f.
1.3. Considere uma função ψ cuja expressão analítica é ψ(x) = af(x − b) + c, a, b, c ∈ R\{0}.
Sabe-se ainda que:
• O gráfico de ψ admite um zero em x = b.
• ψ(b + 4) = 12;
• ψ(1) = 16
Determine uma possível expressão analítica de ψ.
Explique como esboçaria o gráfico de ψ.
SINAL + | Nuno Miguel Guerreiro
Ficha Avaliação Contínua | Matemática A - 10o Ano| 1
