131 Capítulo 9.Corrente Eléctrica e Resistência Até aqui a nossa

Capítulo 9.Corrente Eléctrica e Resistência
Tópicos do Capítulo
9.1. Corrente Eléctrica
9.2. Resistência e Lei de Ohm
9.3. Supercondutores
9.4. Energia Eléctrica e Potência
Até aqui a nossa discussão dos fenómenos eléctricos concentraram-se em cargas em
repouso ou no estudo da electrostática. Consideraremos agora as situações que
envolvem cargas eléctricas em movimento. O termo corrente eléctrica, ou simplesmente
corrente, é usado para descrever o fluxo da carga em alguma região do espaço. A
maioria das aplicações práticas electricidade envolve correntes eléctricas. Por exemplo,
numa lanterna, as cargas fluem através do filamento da lâmpada depois que o
interruptor é ligado. Na maioria das situações comuns, o fluxo de carga ocorre num
condutor, tal como um fio de cobre. É também possível, entretanto, que as correntes
existam fora de um condutor. Por exemplo, um feixe de electrões num tubo da televisão
constitui uma corrente em que a carga flui através do vácuo.
Neste capítulo, apresentaremos o resistor como um novo elemento de circuito.
9.1. Corrente Eléctrica
Sempre que uma carga está fluindo, diz-se que existe uma corrente. Para definir
matematicamente a corrente, suponha que partículas carregadas estão se deslocando
perpendicularmente em relação a uma superfície de área A, como na Figura 9.1. É uma
área poderia ser a área de secção transversal de um fio, por exemplo. A corrente é
definida como a taxa a que a carga eléctrica flui através dessa superfície. Se ∆Q é a
quantidade de carga que atravessa essa área no intervalo de tempo ∆t, a corrente média
Iméd no intervalo de tempo é a razão entre a carga e o intervalo de tempo:
I méd =
∆Q
∆t
(9.1)
Figura 9.1. Cargas em movimento através de uma área A.
131
É possível que a taxa a que a carga flui varie com o tempo. Definimos a corrente
instantânea I como o limite da expressão precedente à medida que ∆t tende à zero:
∆Q dQ
=
∆t → 0 ∆t
dt
I ≡ lim
(9.2)
A unidade SI da corrente é o ampère (A):
1 A = 1 C/s
(9.3)
Isto é, 1 A de corrente é equivalente a 1 C de carga atravessando uma superfície em 1 s.
As partículas que fluem através de uma superfície, como na Figura 9.1, podem
ser carregadas positiva ou negativamente, ou podemos ter dois ou mais tipos de
partículas que se deslocam, com cargas de ambos os sinais no fluxo.
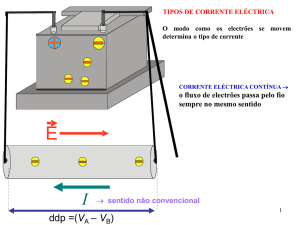
Convencionalmente, definimos a direcção da corrente como a direcção do fluxo de
carga positiva, independentemente do sinal das partículas carregadas reais em
movimento1. Num condutor comum tal como o cobre, a corrente é fisicamente devida
ao movimento dos electrões negativamente carregados. Consequentemente, quando
falamos da corrente em tal condutor, a direcção da corrente é oposta à direcção do fluxo
dos electrões. Por outro lado, se considerarmos um feixe de protões positivamente
carregados num acelerador de partículas, a corrente está na direcção do movimento dos
protões. Em alguns casos, gases e electrólitos, por exemplo, a corrente é o resultado do
fluxo de partículas carregadas positiva e negativamente. É comum a referência a uma
partícula carregada em movimento (positiva ou negativa) como um portador de carga
móvel. Por exemplo, os portadores da carga num metal são os electrões.
Construiremos agora um modelo estrutural que nos permitirá relacionar a
corrente macroscópica ao movimento das partículas carregadas. Considere as partículas
idênticas carregadas que se deslocam num condutor cuja área de secção transversal é A
(Figura 9.2).
Figura 9.2. Uma parte de um condutor cilíndrico uniforme com área de secção
transversal A.
1
Mesmo que falemos em direcção de corrente, esta não é um vector. Correntes somam-se algebricamente
e não vectorialmente.
132
O volume de um elemento do condutor de comprimento ∆xe é V= A∆xe, onde o
subscrito e refere-se ao comprimento do elemento do condutor. Supomos que n
representa o número de portadores móveis de carga (N) por unidade de volume (V),
n=N/V. Assim o número de portadores no elemento de volume é N=nV=nA∆xe e a
carga móvel ∆Q neste elemento é
∆Q= número de portadores × carga por portador = Nq=(nA∆xe)q
onde q é a carga em cada portador2. Se os portadores se deslocam ao longo do
comprimento do condutor e por meio de sua secção transversal com uma velocidade
média constante chamada de velocidade de deriva (drift), vd, a distância que percorrem
num intervalo de tempo ∆t é ∆xd = vd∆t.
Imagine agora que ∆t é escolhido de tal maneira que, durante esse intervalo de
tempo, todos os portadores de carga no elemento do condutor deslocam-se para a direita
de uma distância igual ao comprimento do elemento. Nesse caso ∆xd = ∆xe e ∆xe = vd∆t
Na Figura 9.2, esse processo seria equivalente a mover o cilindro mais escuro para a
direita por uma distância igual a seu comprimento. Fazendo assim, toda a carga contida
no elemento do condutor atravessa a área de secção transversa marcada na Figura 9.2. A
quantidade de carga que atravessa essa área é
∆Q = Nq = (nA∆xe)q = (nAvd∆t)q
Se dividirmos ambos os lados dessa equação pelo intervalo de tempo ∆t durante o qual
ocorre o fluxo de carga, veremos que a corrente no condutor é
I=
∆Q
= nqvd A
∆t
(9.4)
A Equação 9.4 relaciona uma corrente I macroscópica medida com a origem
microscópica da corrente - a densidade dos portadores de carga n, a carga portador q e a
velocidade de deriva, vd.
Investiguemos mais a noção da velocidade de deriva. Nós a identificamos como
uma velocidade média ao longo do fio, mas os portadores de carga não estão se
deslocando de maneira alguma em uma linha recta com velocidade vd. Vamos supor um
condutor em que os portadores de carga são electrões livres. Quando não existe uma
diferença de potencial através do condutor, esses electrões realizam movimento
aleatório similar àquele das moléculas de gás visto anteriormente na teoria cinética
(Termodinâmica). Esse movimento aleatório está relacionado à temperatura do
condutor. Os electrões sofrem repetidas colisões com os átomos do metal e o resultado é
um movimento complicado em ziguezague (Figura 9.4). Quando uma diferença de
potencial é aplicada através do condutor, um campo eléctrico é estabelecido no
condutor. O campo eléctrico exerce uma força eléctricas obre os electrões. Essa força
acelera os electrões e então produz uma corrente. O movimento dos electrões devido à
2
A expressão fluxo de corrente é utilizada vulgarmente, embora estritamente incorrecta, porque a
corrente é um fluxo (de carga). Isso é similar à expressão transferência de calor, que também é
redundante porque o calor é uma transferência (de energia). Evitaremos essa expressão e falaremos de
fluxo de carga.
133
força eléctrica sobreposto ao seu movimento aleatório para fornecer uma velocidade
média cujo módulo é a velocidade de deriva , vd.
A densidade de corrente J no condutor é definida como a corrente por unidade
de área. A partir da equação 9.4, obtemos a densidade de corrente
J≡
I
= nqvd
A
(9.5)
onde J tem as unidades do SI ampères por metro quadrado.
Figura 9.4. Uma representação esquemática do movimento em ziguezague de um
portador de carga em um condutor. As mudanças de sentido são devidas a colisões com
átomos no condutor. Observe que a resultante do movimento dos electrões está na
direcção oposta à direcção do campo eléctrico.
9.2. Resistência e Lei de Ohm
A velocidade de drift dos electrões num fio com corrente está relacionada com o campo
eléctrico no fio - se o campo aumentar, a força eléctrica sobre os electrões é mais forte e
a velocidade de drift aumenta. Para um campo uniforme num condutor de secção
transversal uniforme, a diferença de potencial no condutor é proporcional ao campo
eléctrico (∆V ∝ E). Assim, quando uma diferença potencial ∆V é aplicada nas
extremidades de um condutor metálico, como na Figura 9.5, a corrente observada no
condutor é proporcional à tensão aplicada; isto é, I ∝ ∆V. Podemos escrever essa
proporcionalidade como ∆V = IR, onde a constante de proporcionalidade R é chamada
de resistência do condutor. Definimos essa resistência, de acordo com a equação que
acabamos de escrever, como a razão entre a tensão no condutor e a corrente que ele
transporta:
R≡
∆V
I
(9.6)
A resistência tem a unidade SI de volt por ampère, chamada de ohm (Ω). Assim, uma
diferença de potencial de 1V num condutor produz uma corrente de 1 A, a resistência
do condutor é 1 Ω. Como um outro exemplo, se um dispositivo eléctrico ligado a uma
fonte de 120 V transporta uma corrente de 6.0 A, sua resistência é 20 Ω.
134
Figura 9.5. Um condutor uniforme de comprimento l e área de secção transversal A.
Uma diferença de potencial Vb - Va é mantida no condutor de maneira que existe um
campo eléctrico E no condutor, e este campo produz uma corrente I que é proporcional
à diferença de potencial.
Para muitos materiais, incluindo os metais, experimentos mostram que a
resistência é constante para grande parte das tensões aplicadas. Esse comportamento é
conhecido como lei de Ohm, em homenagem a Georg Simon Ohm (1787-1854), que foi
o primeiro a fazer um estudo sistemático da resistência eléctrica.
A lei de Ohm não é uma lei fundamental da natureza, mas uma relação empírica
válida somente para determinados materiais e dispositivos, sob uma escala limitada de
condições. Os materiais ou os dispositivos que obedecem à lei de Ohm, e portanto, têm
uma resistência constante numa vasta escala de tensões, são chamados de óhmicos. Os
materiais ou dispositivos que não obedecem à Ohm são chamados de não – óhmicos.
Figura 9.6. (a) A curva da corrente em função da tensão para um dispositivo óhmico. A
curva é linear e a inclinação fornece a resistência do condutor. (b) Uma curva não linear
da corrente em função da tensão para um díodo semicondutor. Esse dispositivo não
obedece à lei de Ohm.
135
Os materiais ou dispositivos óhmicos tem uma relação linear entre a tensão e a corrente
numa ampla gama de tensões aplicadas, como mostra a representação gráfica na Figura
9.6a. Os materiais ou dispositivos não – óhmicos têm uma relação não linear entre a
corrente e a tensão, como mostra a Figura 9.6b. O díodo é um dispositivo semicondutor
comum não – óhmico, sendo um elemento de circuito que age como uma válvula de
sentido único para a corrente. Sua resistência é pequena para correntes num sentido (∆V
positivo), e grande para correntes no sentido inverso (∆V negativo). A maioria dos
dispositivos electrónicos modernos, tais como transístores, tem relações não lineares
entre a corrente e a tensão. A operação destes dispositivos depende da maneira
particular com que violam a lei de Ohm3.
Um resistor é um elemento simples do circuito que fornece uma resistência
especificada num circuito eléctrico. O símbolo para um resistor em diagramas de
circuito é uma linha em ziguezague
Podemos expressar a equação 9.6 na forma
∆V ≡ RI
(9.7)
Essa equação nos diz que a tensão num resistor é o produto da resistência e da corrente
no resistor.
A resistência de um fio condutor óhmico é proporcional ao seu comprimento e
inversamente proporcional à sua área de secção transversal. Assim:
R=ρ
l
A
(9.8)
onde a constante de proporcionalidade ρ é chamada de resistividade do material que
tem as unidades ohm-metro ( Ω ⋅ m ). Cada material óhmico tem uma resistividade
característica, um parâmetro que depende das propriedades do material e da
temperatura. Por outro lado, como se pode ver a partir da equação 9.8, a resistência de
um condutor depende de seu tamanho e de sua forma, bem como da resistividade do
material.
O inverso da resistividade é definido como a condutividade σ (σ=1/ρ). Portanto,
a resistência de um condutor óhmico pode ser expressa em termos de sua condutividade
como
R=
l
σA
(9.9)
σ tem a unidade ( Ω ⋅ m )-1.
3
A Equação 9.6 não é a lei de Ohm. Essa equação é simplesmente a definição de resistência e fornece
uma relação importante entre tensão, corrente e resistência. A lei de Ohm refere-se à relação linear entre
corrente e tensão, ( ∆V ≡ RI ) e que, a partir da equação 9.6, indica que a resistência é constante,
independentemente da tensão aplicada.
136
9.3. Supercondutores
Para uma classe de metais e de compostos conhecidos como supercondutores, a
resistência vai a zero abaixo de uma determinada temperatura crítica Tc. O gráfico da
temperatura em função da resistência para um supercondutor segue o gráfico de um
metal normal em temperaturas acima de Tc. Quando a temperatura alcança Tc, a
resistividade cai repentinamente a zero (Figura 9.7). Esse fenómeno foi descoberto pelo
físico holandês Heike Kamerlingh Onnes em 1911 quando trabalhava com mercúrio,
que é um supercondutor abaixo de 4.2 K Medidas recentes mostraram que as
resistividades dos supercondutores abaixo de Tc são menores do que 4 × 10-25 Ω ⋅ m ,
que é aproximadamente 1017 vezes menor do que a resistividade do cobre e considerada
como nula na prática.
Figura 9.7. O gráfico à esquerda mostra a resistência em função da temperatura para
uma amostra de mercúrio. A resistência cai à zero à Tc de 4.2 K para o mercúrio. A
Figura à direita mostra um pequeno íman permanente que levita sobre um disco
supercondutor.
Actualmente, milhares de supercondutores são conhecidos. Metais comuns como
o alumínio, o estanho, o chumbo, o zinco e o índio são supercondutores. A Tabela 9.1
lista as temperaturas críticas de diversos supercondutores. O valor de Tc é sensível à
composição química, à pressão e à estrutura cristalina. É interessante notar que o cobre,
a prata e o ouro, que são condutores excelentes à temperatura ambiente, não apresentam
supercondutividade. Uma das características verdadeiramente notáveis dos
supercondutores é o facto que, uma vez que uma corrente é criada neles, ela persiste
sem nenhuma tensão aplicada (porque R = 0). De fato, observou-se que correntes
permanentes persistem em espiras supercondutoras por diversos anos sem nenhum
decaimento aparente. Um desenvolvimento importante na física, que criou grande
excitação na comunidade científica na última parte do século XX, foi a descoberta de
supercondutores de altas temperaturas baseados em óxidos de cobre (até 137 K).
Actualmente, não podemos descartar a possibilidade de supercondutividade à
temperatura ambiente e a busca por novos materiais supercondutores continua. É uma
busca importante por razões científicas uma vez que as aplicações práticas se tornam
mais prováveis e difundidas à medida que a temperatura crítica é elevada.
137
Tabela 9.1.
9.4. Energia Eléctrica e Potência
Se uma bateria é usada para criar uma corrente eléctrica num condutor, há uma
transformação contínua da energia química na bateria em energia cinética dos electrões
e em energia interna no condutor, tendo como consequência um aumento na
temperatura do condutor.
Figura 9.8. Circuito eléctrico.
Em circuitos eléctricos típicos, a energia é transferida de uma fonte, tal como
uma bateria, para algum dispositivo, como por exemplo uma lâmpada ou um receptor de
rádio. Vamos determinar uma expressão que nos permita calcular a taxa dessa
transferência de energia. Em primeiro lugar, considere o circuito simples na Figura 9.8,
no qual imaginamos que a energia esteja sendo transferida para um resistor. Como os
fios de conexão também têm resistência, parte da energia vai para os fios e parte da
138
energia vai para o resistor. Adoptaremos um modelo simplificado em que a resistência
dos fios é tão pequena comparada com a resistência do elemento de circuito que
desprezaremos a energia transferida para os fios.
Analisemos agora a transferência de energia do circuito em que uma bateria é
ligada a um resistor de resistência R, como na Figura 9.8. Imagine que seguimos o
percurso de uma quantidade positiva da carga Q em torno do circuito a partir do ponto
a, passando através da bateria e do resistor, e voltando para a. O ponto a é um ponto de
referência no qual o potencial é definido como zero. Identificamos o circuito inteiro
como nosso sistema. Quando a carga vai de a para b através da bateria, cuja diferença
de potencial é ∆V, a energia potencial eléctrica (U) do sistema aumenta em Q∆V e a
energia química na bateria diminui na mesma quantidade. Contudo, quando a carga se
desloca de c para d através do resistor, o sistema perde essa energia potencial eléctrica
durante as colisões com os átomos no resistor. Nesse processo, a energia é transformada
em energia interna correspondente ao aumento do movimento vibracional dos átomos
no resistor. Como desprezamos a resistência dos fios de ligação, nenhuma
transformação de energia ocorre nos trechos bc e da. Quando a carga retoma ao ponto a,
o resultado líquido é que parte da energia química na bateria foi para o resistor e
permanece nele como energia interna associada com a vibração molecular.
O resistor está normalmente em contacto com o ar, de modo que o aumento da
sua temperatura resulta em transferência de energia pelo calor para o ar. Além disso a
radiação térmica ocorre a partir do resistor, representando um outro meio de perda de
energia. Depois de passado algum tempo, o resistor permanece a uma temperatura
constante, quando a entrada da energia proveniente da bateria é equilibrada pela saída
da energia pelo calor e pela radiação. Alguns dispositivos eléctricos incluem
dissipadores de calor conectados em algumas partes do circuito para impedir que estas
alcancem temperaturas perigosamente altas. Esses dispositivos são constituídos por
partes metálicas com muitas aletas. A condutividade térmica elevada do metal fornece
transferência rápida da energia pelo calor para longe da componente quente e as várias
aletas fornecem uma grande área de contacto com o ar, de modo que a energia possa ser
transferida pela radiação e para o ar pelo calor rapidamente.
Consideremos agora a taxa a que o sistema perde energia potencial eléctrica
quando a carga Q atravessa o resistor:
onde I é a corrente no circuito. Naturalmente, o sistema recobra essa energia potencial
quando a carga atravessa a bateria, à custa da energia química da bateria. A taxa a que o
sistema perde energia potencial quando a carga atravessa o resistor é igual à taxa a que o
sistema ganha energia interna no resistor. Assim, a potência P representando a taxa a
que a energia é fornecida para o resistor, é dada por
P = I∆V
(9.10)
Desenvolvemos esse resultado considerando uma bateria fornecendo energia para um
resistor. Entretanto, a equação 9.10 pode ser usada para determinar a potência
transferida de uma fonte de tensão para qualquer dispositivo que transporta uma
corrente I e tem uma diferença de potencial ∆V entre seus terminais.
139
Usando a equação 9.10 e o fato de que ∆V = IR para um resistor, podemos
expressar a potência entregue ao resistor de outras formas
P = I 2R =
(∆V )2
R
(9.11)
A unidade SI de potência é o watt que corresponde a J/s. A potência fornecida a um
condutor de resistência R é frequentemente chamada de uma perda I2R.
140