QUESTÃO 2 A resistência de um fio condutor pode ser

QUESTÃO 2
A resistência de um fio condutor pode ser calculada de acordo com a
seguinte equação, (Alexander e Sadiku, 2010):
𝑅=
𝜌. 𝑙
𝐴
[Ω],
em que: 𝜌 é a resistividade do material condutor, 𝑙 é o comprimento do fio e 𝐴 é
área da seção transversal desse fio.
Dessa forma, pode-se concluir o seguinte:
𝑅 ∝ 𝑙,
ou seja, a resistência de um fio elétrico é proporcional ao seu comprimento.
A Questão 2 pede para calcular o valor da resistência entre os pontos A
e B, sendo que esse fio é ligado com dois seguimentos iguais entre os pontos
A e C e 2 seguimentos iguais entre os pontos B e C e o comprimento do
seguimento 𝐴𝐶 é L/10.
SOLUÇÃO
As resistências dos fios ligados conforme apresentado na Figura 2
(Questão 2) podem ser representadas por resistores conforme o circuito
abaixo:
Figura 1: Circuito equivalente ao esquema apresentado na Figura 2(da Questão 2).
1
em que 𝑅1 = 𝑅2 e 𝑅3 = 𝑅4, pois a resistividade do material e a sua seção
transversal não foi modificada, sendo modificadas somente as distâncias entre
os pontos A e C e C e B, ou seja, o comprimento do fio.
Como 𝐴𝐶 = 𝐿/10, tem-se que 𝐶𝐵 = 𝐿 − 𝐿/10 = 9𝐿/10.
Como a resistência é proporcional ao comprimento, ficando os demais
parâmetros constantes, o valor das resistências equivalentes (𝑅𝑒𝑞 ) das
associações dos resistores apresentados na Figura 1 podem ser obtidos como
se segue:
𝑅𝑒𝑞 1 = 𝑅1||𝑅2 (seguimento 𝐴𝐶 )
𝑅𝑒𝑞 1
𝐿
𝐿
× 10
𝐿
10
∝
=
𝐿
𝐿
20
+
10 10
𝑅𝑒𝑞 2 = 𝑅3||𝑅4 (seguimento 𝐶𝐵)
𝑅𝑒𝑞 1
9𝐿 9𝐿
×
9𝐿
∝ 10 10 =
9𝐿 9𝐿 20
10 + 10
A resistência total do fio elétrico será dada pela associação em série de
𝑅𝑒𝑞 1 e 𝑅𝑒𝑞 2 :
𝑅 𝐴𝐵 = 𝑅𝑒𝑞 1 + 𝑅𝑒𝑞 2
𝑅𝐴𝐵 ∝
𝐿 9𝐿
+
20 20
𝑅𝐴𝐵 ∝
10𝐿
20
𝑅𝐴𝐵 ∝
𝐿
2
2
Se a resistência inicial do fio elétrico era 𝑅 com (𝑅 ∝ 𝐿), a resistência
final será de
𝑅
2
com (𝑅 ∝ 𝐿/2). Dessa forma, a opção correta é letra C.
QUESTÃO 8
De acordo com a norma NBR 5410:2008:
6.2.6.2 Condutor neutro
6.2.6.2.1 O condutor neutro não pode ser comum a mais de um circuito.
6.2.6.2.2 O condutor neutro de um circuito monofásico deve ter a mesma seção
do condutor de fase.
6.2.6.2.3 Quando, num circuito trifásico com neutro, a taxa de terceira
harmônica e seus múltiplos for superior a 15%, a seção do condutor neutro não
deve ser inferior à dos condutores de fase, podendo ser igual à dos condutores
de fase se essa taxa não for superior a 33%.
NOTAS
1 Tais níveis de correntes harmônicas são encontrados, por exemplo, em
circuitos que alimentam luminárias com lâmpadas de descarga, incluindo as
fluorescentes.
2 O caso de taxas superiores a 33% é tratado em 6.2.6.2.5.
6.2.6.2.4 A seção do condutor neutro de um circuito com duas fases e neutro
não deve ser inferior à seção dos condutores de fase, podendo ser igual à dos
condutores de fase se a taxa de terceira harmônica e seus múltiplos não for
superior a 33%.
NOTA O caso de taxas superiores a 33% é tratado em 6.2.6.2.5.
6.2.6.2.5 Quando, num circuito trifásico com neutro ou num circuito com duas
fases e neutro, a taxa de terceira harmônica e seus múltiplos for superior a
33%, pode ser necessário um condutor neutro com seção superior à dos
condutores de fase.
3
NOTAS
1 Tais níveis de correntes harmônicas são encontrados, por exemplo, em
circuitos que alimentam principalmente computadores ou outros equipamentos
de tecnologia de informação.
2 Para se determinar a seção do condutor neutro, com confiança, é necessária
uma estimativa segura do conteúdo de terceira harmônica das correntes de
fase e do comportamento imposto à corrente de neutro pelas condições de
desequilíbrio em que o circuito pode vir a operar. O anexo F fornece subsídios
para esse dimensionamento.
6.2.6.2.6 Num circuito trifásico com neutro e cujos condutores de fase tenham
uma seção superior a 25 mm2 , a seção do condutor neutro pode ser inferior à
dos condutores de fase, sem ser inferior aos valores indicados na tabela 48,
em função da seção dos condutores de fase, quando as três condições
seguintes forem simultaneamente atendidas: a) o circuito for presumivelmente
equilibrado, em serviço normal; b) a corrente das fases não contiver uma taxa
de terceira harmônica e múltiplos superior a 15%; e c) o condutor neutro for
protegido contra sobrecorrentes conforme 5.3.2.2.
NOTA Os valores da tabela 48 são aplicáveis quando os condutores de fase e
o condutor neutro forem do mesmo metal.
 A assertiva 𝚰 da QUESTÃO 8 diz o seguinte:
Para o dimensionamento da seção do condutor neutro em função da
terceira harmônica (THD3) e suas múltiplas, são consideradas as seguintes
faixas: 𝑇𝐻𝐷3 < 15%, 15% ≤ 𝑇𝐻𝐷3 ≤ 33% e 𝑇𝐻𝐷3 > 30%.
Pode-se verificar na norma NBR 5410:2008 que em nenhum momento é
citada a taxa de distorção harmônica THD3 de 30%. Portanto, a assertiva Ι está
errada.
QUESTÃO 14
Esta questão fornece os seguintes dados dos equipamentos:
4

PN é a potência nominal (mecânica) em [cv];

VN é a tensão nominal em [V];

FP é o fator de potência;

R é o rendimento;

O valor do fator de utilização é 𝐹𝑢 = 0,8;

O fator de simultaneidade é 𝐹𝑠 = 0,85.
SOLUÇÃO
O fator de utilização é o fator que deve ser multiplicada a potência
nominal do equipamento para se obter a potência média absorvida pelo
mesmo, (Mamede Filho, 2010).
O fator de simultaneidade é a relação entre a demanda máxima do
grupo de aparelhos pela soma das demandas individuais dos aparelhos do
mesmo grupo num intervalo de tempo considerado, (Mamede Filho, 2010).
O cálculo da demanda solicitada da rede de energia pelos motores pode
ser calculada por meio da equação (1):
𝐷=
𝑃𝑒𝑖𝑚 × 736
𝜂 × 𝐹𝑃
[VA],
(1)
em que: D é a demanda solicitada da rede de energia, 𝑃𝑒𝑖𝑚 é a potência no
eixo do motor, 𝜂 é o rendimento do motor e FP é o fator de potência.
A potência no eixo do motor é calculada por meio da equação (2):
𝑃𝑒𝑖𝑚 = 𝑃𝑁 × 𝐹𝑢
[cv].
(2)
Na equação (1), ao multiplicar a potência 𝑃𝑒𝑖𝑚 (em cv) por 736 está
realizando a conversão de cv para W(watt). A potência em watt é a potência
ativa. Quando se divide a potência ativa pelo fator de potência tem-se a
potência aparente, cuja unidade é volt-ampère (VA). Este conceito pode ser
deduzido da própria equação do cálculo do fator de potência, como
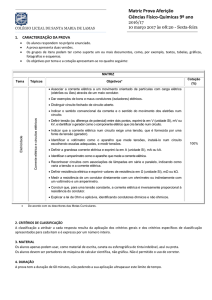
apresentado na equação (3) e da Figura 1:
𝐹𝑃 =
𝑝𝑜𝑡ê𝑛𝑐𝑖𝑎 𝑎𝑡𝑖𝑣𝑎 (𝑊)
𝑝𝑜𝑡ê𝑛𝑐𝑖𝑎 𝑎𝑝𝑎𝑟𝑒𝑛𝑡𝑒 (𝑉𝐴)
(3)
5
Figura 2: Triângulo de Potências.
Dessa forma tem-se:
𝑝𝑜𝑡𝑒𝑛𝑐𝑖𝑎 𝑎𝑝𝑎𝑟𝑒𝑛𝑡𝑒 =
𝑝𝑜𝑡ê𝑛𝑐𝑖𝑎 𝑎𝑡𝑖𝑣𝑎
𝐹𝑃
Sendo que 𝐹𝑃 = 𝑐𝑜𝑠𝜙.
Contudo, aplicando os valores apresentados na Questão 14, tem-se:
1) Demanda dos tornos (2 tornos):
𝐷=
0,8 × 5 × 736
= 4618,0392 𝑉𝐴
0,85 × 0,75
𝐷 = 2 × 4618,04 = 9236,0784 𝑉𝐴
2) Demanda do bebedouro:
𝐷=
0,8 × 0,5 × 736
= 646,1808 𝑉𝐴
0,67 × 0,68
3) Demanda das fresas (3 fresas):
𝐷=
0,8 × 3 × 736
= 2730,9833 𝑉𝐴
0,84 × 0,77
𝐷 = 3 × 2730,98 𝑉𝐴 = 8192,9499 𝑉𝐴
4) Demanda da plaina:
𝐷=
0,8 × 2 × 736
= 1970,5488 𝑉𝐴
0,83 × 0,72
𝐷=
0,8 × 1 × 736
= 1154,5098 𝑉𝐴
0,75 × 0,68
5) Demanda da serra:
6) Demanda da bancada de trabalho:
6
𝐷 = 1800𝑉𝐴
7) Demanda da iluminação:
𝐷 = 3400𝑉𝐴
O fator de simultaneidade fornecido foi de 𝐹𝑠 = 0,85, assim a demanda
total dos motores foi de:
𝐷𝑚𝑜𝑡𝑜𝑟𝑒𝑠
𝑡𝑜𝑡𝑎𝑙
= 0,85 × 9236,0784 + 646,1808 + 8192,9499 + 1970,5488 + 1154,5098
𝐷𝑚𝑜𝑡𝑜𝑟𝑒𝑠
𝑡𝑜𝑡𝑎𝑙
= 18020,2275 𝑉𝐴
Dessa forma, a demanda total solicitada pelo setor considerado será de:
𝐷𝑡𝑜𝑡𝑎𝑙 = 18020,2275 + 1800 + 3400 = 23220,2 𝑉𝐴 = 23,22 × 103 = 23,22𝑘𝑉𝐴
Contudo, a única questão possível seria letra A: 23,8𝑘𝑉𝐴.
REFERÊNCIAS BIBLIOGRÁFICAS
Alexander, Charles; Sadiku, Matthew N. O. Fundamentos de Circuitos Elétricos.
5ª edição, 2013, Editora McGraw-Hill.
Mamede Filho, João. Instalações Elétricas Industriais. 8ª edição, 2010, Editora
LTC.
NBR 5410 Instalações elétricas de baixa tensão: procedimentos. Rio de
Janeiro: ABNT, 2008.
7