Aula 3: Revisão de Movimento uniforme e exercícios


Escalares:ficam bem caracterizadas apenas falandose sobre seu módulo como massa, área, volume ,
densidade,tempo, energia,etc.


Vetoriais:é necessário que se defina além do módulo,
direção e sentido dessa grandeza, como velocidade, força,
aceleração,quantidade de movimento, entre outros
Para se representar uma grandeza vetorial deve-se
colocar uma seta sobre a letra que representa essa
grandeza

Interprete fisicamente a piada da figura abaixo:

Trata-se da velocidade hipotética que um corpo teria
se fizesse seu percurso com velocidade constante. Sua
equação é



m/s e Km/h são as mais comuns;
m/s (ou m.s-1);
km/h (ou km.h-1);
cm/s, (cm.s-1);
A usada no SI é o m/s
Exemplos:
 20m/s  20 x 3,6 = 72  72Km/h


De Km/h para m/s dividimos por 3,6.Exemplo:
 72Km/h  72/3,6 = 20  20m/s

Quem se move mais rápido? Um navio a 20m/s ou um
a 36Km/h?

É possível que os veículos abaixo possuam mesma
velocidade escalar média?

O ΔS só representa a distância que o móvel percorreu
se ele não inverter seu sentido de movimento.

Se o móvel fizer uma trajetória e depois voltar a posição
inicial por meio dessa mesma trajetória, após inverter o
movimento, o ΔS será 0 e a velocidade média também.

Num movimento em trajetória fechada sem inversão de
sentido, o ΔS será igual a distância percorrida. Se for em
uma circunferência completa, o ΔS será 2πR.

O que representa uma velocidade de 3m/s? E de
100Km/h?


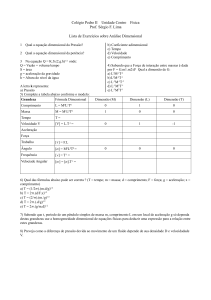
Equação dimensional de uma grandeza física é aquela
que pode ser escrita em função do comprimento L e
do tempo T (para os assuntos de dinâmica, aparece
também a massa M).
A equação dimensional é simbolizada por um
colchete:[G] (lê-se equação dimensional de G).Temos a
equação abaixo onde x e y são chamados de dimensões
de G em relação a L e a T:
x
y
[G]:L T

A equação dimensional da velocidade escalar é:
4320m
9x60=540s