2. CONCEITOS BÁSICOS

2. CONCEITOS BÁSICOS
O objetivo deste capítulo é fazer uma breve revisão de conceitos vistos em disciplinas da grade fundamental
e que serão de utilidade nesta disciplina.
ENERGIA
O objetivo de utilizar uma máquina de fluxo hidráulica é realizar a troca de energia entre fluido e
equipamento. De modo que se torna importante quantificar esta troca.
Para obter este valor de energia aplica-se a 1ª lei da termodinâmica a um volume de controle. A Figura 2.1
indica as fronteiras físicas de uma máquina de fluxo hidráulica, que pode ser motora ou geradora.
Figura 2.1 - Volume de controle
A Figura 2.1 mostra o volume de controle cujas fronteiras coincidem com as delimitações físicas da máquina
de fluxo (M.F.). As seções de entrada e descarga são representadas pelos subíndices “e” e “s” respectivamente.
Considerando propriedades uniformes nas seções de entrada e saída, tem-se:




dE
V2
V2
 Q  W   m e  he  e  gz e    m s  hs  s  gz s 
dt
2
2
e

 s


onde:
Q – taxa de energia recebida na forma de calor [J/s]
W – taxa de energia fornecida na forma de trabalho [J/s]
h – Entalpia [J/kg]
m - vazão mássica [kg/s]
V – velocidade média do fluido [m/s]
2
g – aceleração da gravidade [m/s ]
z – cota em relação a uma referência arbitrária [m]
Considerando regime permanente e somente uma entrada e uma saída:




V2
V2
0  Q  W  m e  he  e  gz e   m s  hs  s  gz s 
2
2




Aplicando o princípio da conservação da massa ao volume de controle, considerando regime permanente e
somente uma entrada e uma saída,
dmVC
  m e   m s  m e  m s  m
dt
2-1
Aplicando à equação da energia,

 

V2
V2
Q  W  m  hs  s  gz s    he  e  gz e  
2
2
 


Considerando “Y” como a energia por unidade de massa (J/kg) cedida pela máquina na forma de trabalho, e
“q” a energia por unidade de massa (J/kg) recebida pela máquina na forma de calor, resulta:
 V 2  Ve2 
  g  z s  z e 
q  Y  hs  he    s
2


Para bombas hidráulicas (hydraulic pumps) e ventiladores (fans), considerando:
Transformação adiabática (q=0) e sem atrito (isentrópica)  s3  s 2  ds  0
Trabalho recebido pelo sistema é negativo (convenção termodinâmica)
o
o
Considerando “T” a temperatura absoluta (em K) e “s” a entropia (em J/kg.K) e lembrando que:
dq = Tds = dh - vdp
Das considerações anteriores (ds=0):
dh  vdp 

s
e
dh 

s
e
s
s
e
e
 cte
vdp v
  dh  v  dp  hs  he  v ( p s  p e ) 
p s  pe

Resulta,
Y 
p s  pe 1 2
 V s  V e2  g  z s  z e 

2


(2.1)
Ao utilizar a Eq.(2.1) para calcular a energia (por unidade de massa) em forma de trabalho (Y) entregue à
bomba/ventilador, o valor obtido será negativo. Isto está em conformidade com nossa convenção termodinâmica de
que a energia que entra no volume de controle em forma de trabalho é negativa. Como nosso interesse é quantificar
o valor desta energia e já temos ciência de que ela entra no volume de controle, que é entregue ao equipamento,
deixaremos seu valor positivo. Além disto, dividiremos a equação pela aceleração da gravidade (g) para obter a
energia por unidade de peso (H) cuja unidade é [J/N], dada por:
H 
ps  pe
1

V s2  V e2   z s  z e 

2g


(2.2)
Para turbinas hidráulicas (hydraulic turbines), considerando:
o
o
Transformação adiabática (q=0) e sem atrito (isentrópica)  s3  s 2  ds  0
Trabalho entregue pelo sistema é positivo (convenção termodinâmica)
Aplicando as hipóteses acima à equação da energia tem-se o mesmo desenvolvimento dado para bombas,
chegando-se à mesma Eq.(2.1). Que resulta,
H
pe  p s
1

Ve2  Vs2   z e  z s 

2g


(2.3)
2-2
VAZÃO
A mecânica dos fluidos define vazão volumétrica [m3] como o volume de fluido que atravessa dada seção
transversal qualquer na unidade de tempo; e vazão mássica a quantidade de massa [kg] que passa nesta seção na
unidade de tempo, sendo esta última escrita como:
 
m   V .dA
SC
Considerando que “A” é a área da seção transversal do tubo, “V” a velocidade média do escoamento na
seção transversal do tubo tratada e “” a massa específica do fluido, que para as máquinas hidráulicas é constante, e
fazendo a integração tem-se que a taxa mássica será:
  VA
m
(2.4)
Enquanto a vazão volumétrica é dada por:
(2.5)
m
Q  V   VA

Medidores de Vazão de Restrição para escoamentos internos
Segundo Fox & MacDonald (2001, p. 249) a maioria dos medidores de restrição para escoamentos internos
baseiam-se no princípio da aceleração da corrente fluida através de alguma forma de bocal.
A equação geral dos medidores de orifício pode ser escrita como:
Q  C Q Am 2 gH
(2.6)
Onde:

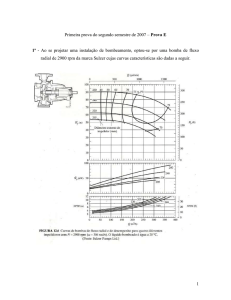
“Cq” vem de gráficos (Fig.2.2) e é função de Reynolds e “m”,
A
d
m m  
At  D 




2
Am é a área de seção, de diâmetro “d”, do medidor,
At é a área da seção de entrada (do tubo), de diâmetro “D”,
“g” a aceleração da gravidade, e
“ΔH” a diferença de pressão (em m) no medidor, ou a perda de carga (em m).
Outras relações para definição dos coeficientes de vazão podem ser vistas em Fox & MacDonald (2001,
p.249-257).
2-3
Figura 2.2 - Valores de “CQ” para alguns medidores de vazão
2-4
Rotação
Para máquinas geradoras (bombas e ventiladores) a rotação é fornecida pelo motor de acionamento. Se for
elétrico podem ser os de corrente alternada (C.A.) ou de corrente contínua (C.C.). Existem alternativas aos motores
elétricos; bombas de sistemas de incêndio, por exemplo, são normalmente acionadas por motores diesel.
Os motores elétricos C.C. têm sua velocidade determinada pela tensão de alimentação. Apresentam torque
constante em praticamente toda sua faixa de velocidade.
Motores elétricos C.A. são divididos entre síncronos e assíncronos (indução). Os motores síncronos
trabalham na rotação síncrona, já o assíncrono tem uma perda de velocidade devido a um fenômeno chamado
escorregamento, que faz com que operem em rotações pouco mais baixas que a rotação síncrona. Os motores
elétricos C.A. mais comuns tem 1 e 2 pares de pólos, e suas rotações são: de 3600 rpm e 1800 rpm para os síncronos,
e de 3500 rpm e 1750 rpm para os assíncronos.
Caso seja necessário ter uma rotação diferenciada da rotação dos motores C.A. pode-se utilizar acionamento
por correia, por engrenagens ou outro tipo de redutor ou amplificador de rotação. Em motores de C.C. isto é feito
eletronicamente.
As máquinas motoras (turbinas) são geralmente acopladas a alternadores (geradores de C.A.) que devem
trabalhar com rotações síncronas constantes. Essa rotação síncrona depende do número de pares de pólos do
gerador e da frequência da rede elétrica a qual está ligada a máquina.
A rotação síncrona (nsinc) é dada por:
nsinc 
f .60
p
 f-freqüência da rede (Brasil - 60 Hz);
 p-número de pares de pólos do alternador;
 n-rotação síncrona.
Perdas de Carga
As perdas de carga em tubos e acessórios podem ser calculadas com alguns métodos:
Hazen-Willians1:
É um método empírico muito utilizado, que apresenta resultados razoáveis para tubos com diâmetros de 50
mm a 3000 mm, velocidades inferiores a 3,0 m/s e escoamento com água. O sucesso de sua utilização depende,
dentre outros fatores, da correta avaliação do coeficiente “C”.
H pc  10,643.Q1,85 .C 1,85 .D4,87 .L
(2.7)
Onde:





3
Q – vazão [m /s]
Hpc – perda de carga na tubulação forçada [m]
C – coeficiente de Hazen-Willians (Tabelas 2.1 e 2.2)
D – diâmetro interno da tubulação [m]
L – comprimento da tubulação reta [m]
1
Relação empírica desenvolvida no início do século XX e ainda bastante utilizada. Atualmente, com as facilidades de uso
de planilhas computacionais, calculadoras científicas, e outros, a formulação dada por Darcy-Weisbach para cálculo de perda de
carga é uma opção mais apropriada.
2-5
Tabela 2.1 – Coeficientes de Hazen-Williams
Tabela 2.2 – Coeficientes de Hazen-Williams [Fonte: KSB, 2001]
2-6
Darcy-Weisbach:
Válida para fluidos incompressíveis. Tem a seguinte forma para cálculos de perdas em trechos retos de
tubos:
H pc  f .
LV2
D 2g
(2.8)
Onde:





f – coeficiente de atrito, que vem do diagrama de Moody-Rouse
Hpc – perda de carga na tubulação [m]
D – diâmetro interno da tubulação [m]
L – comprimento da tubulação [m]
V – velocidade média [m/s]
Outra forma de obter o coeficiente de atrito, sem precisar do diagrama de Moody-Rouse é usando a fórmula
de Colebrook, que considera a rugosidade do tubo (e) e o número de Reynolds (Re) do escoamento:
1
f 0,5
e
2,51 
 2,0. log D 
 3,7 Re . f 0,5 


(2.9)
O inconveniente é que tal fórmula requer um processo iterativo para obtenção de “f”. Porém, segundo
Miller (Fox & MacDonald, 2001), se o valor inicial de “f” no processo iterativo for obtido com o uso da eq.(2.7), com
uma ou duas iterações obtêm-se um erro menor que 1%:
 e

5,74 

D

f 0  0,25. log

  3,7 Re 0,9 

 
2
(2.10)
Sendo o número de Reynolds obtido por:
Re 





V D V D



(2.11)
ρ – massa específica [kg/m3]
V – velocidade média do escoamento [m/s]
D – diâmetro do tubo [m]
μ - viscosidade dinâmica [Pa.s]
2
ν - viscosidade cinemática [m /s]
Para perdas localizadas
H pc  k .

V2
2g
(2.12)
k – coeficiente de perda
2-7
Tabela 2.3 – Rugosidade [Fonte: KSB, 2001]
Tabela 2.4 – Coeficiente de perda localizada [Fonte: KSB, 2001]
Tabela 2.5 – Coeficiente de perda localizada [Fonte: KSB, 2001]
2-8
Tabela 2.6 – Coeficiente de perda localizada [Fonte: KSB, 2001]
Método do comprimento equivalente :
Este método tem como objetivo relacionar perdas de carga localizadas a perdas de tubo reto. Espera-se
definir, por exemplo, que comprimento de tubo reto teria a mesma perda de carga que uma válvula (ou outro
acessório) de mesmo diâmetro. A este comprimento chama-se “comprimento equivalente” (Lequivalente). Exemplo: um
registro de gaveta aberto de 1” tem perda de carga equivalente a 0,2 m de tubo reto de 1” (ver tabela 2.7).
Isto assume que uma tubulação que possui ao longo de sua extensão uma série de singularidades (perdas
localizadas) é equivalente a uma tubulação reta de comprimento maior (sem singularidades). Com base neste
conceito o que se faz é adicionar ao comprimento de tubo reto “reto” (Lreto) da tubulação os comprimentos
equivalentes (Lequivalente) dos acessórios.
Nas fórmulas de Hazen-Williams (Eq.2.7) e de Darcy Weisbach (Eq. 2.8) o termo “L” corresponde a tubo reto,
então o que se faz neste caso é considerar:
L  Lreto  Lequivalente
(2.13)
2-9
Tabela 2.7 – Comprimentos equivalentes [Fonte: KSB, 2001]
2-10
Exercícios
3
1. Pede-se calcular a perda de carga na sucção e no recalque do sistema a seguir, considerando que a vazão é de 10 m /h e a
viscosidade cinemática da água de 10-6 m2/s. Utilize o método de Hazen-Willians e Darcy Weisbach. Considere uma
tubulação nova de aço galvanizado. (R. Darcy: 0,8067 mca e 36,227 mca; Hazen: 0,8147 mca e 36,243 mca).
Singularidades:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Filtro: perda de carga de 0,7 mca na vazão especificada
Filtro: perda de carga de 0,7 mca na vazão especificada
Registro de gaveta
Bomba hidráulica
Trocador de calor com perda de carga de 7,0 mca na vazão especificada
Torre de resfriamento
Curva de 90º (R/D=1,5)
Canalização de recalque com diâmetro de 2,5” e comprimento reto de 25 m
Canalização de sucção com diâmetro de 3” e comprimento reto de 10 m
Bicos injetores que funcionam com pressão de 28 mca
Entrada de canalização normal
2. Pede-se calcular a vazão sabendo que a pressão diferencial medida em manômetro acoplado no bocal de vazão é de 1,0 mca.
Sabe-se que o diâmetro da tubulação é de 2” e que o diâmetro do medidor é de 37,8 mm. O escoamento tem Reynolds
5
3
maior que 2.10 . (R. 20 m /h)
3. Sabendo que determinada máquina de fluxo tem vazão de 0,020 m3/s, diâmetro de entrada de 0,1 m e de saída de 0,075 m,
pressões na entrada e saída de 2 mca e 40 mca respectivamente, e o desnível entre a entrada e a saída de 0,15 m, com a entrada abaixo da
saída. Pede-se determinar se tal máquina de fluxo é geradora ou motora. (R. Geradora)
REFERÊNCIAS BIBLIOGRÁFICAS:
FOX, R.W.; MACDONALD, A.T. Introdução à mecânica dos fluidos. 5ª Ed. Rio de Janeiro: Ed. LTC, 2001.
KSB. Manual de Treinamento – Seleção e aplicação de bombas centrífugas. 4ª Ed. 2001.
2-11