Exercícios sobre polarização de bipolares

Mestrado Integrado em Engenharia Electr
Electrónica e Informática /Ano Lectivo 2009/2010
Exercícios sobre Polarização
ão de transístores
Análise de circuitos em DC
I
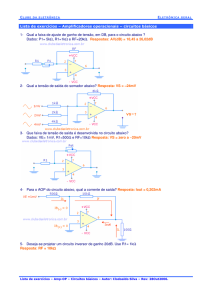
ircuito representado na Figura 11.. Calcule as tensões de polarização,
Considere o circuito
V1,V2,V3,V4, e V5. Assuma que ambos os transístores tem um β=100.
+10V
9.1KΩ
V2
V1
5.1KΩ
V5
V3
100
KΩ
Ω
V4
9.1KΩ
4.3KΩ
-10V
Figura 1.
II
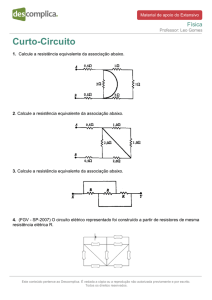
Considere o circuito representado na Figura 2. Os transistores Q1 e Q2 estão a funcionar
na região activa com VBE=VBE=0.7V, β1=100 e β2=50.
a) Calcule as correntes IB2, I1, I2, IC2,IB1, IC1 e IE1
b) Calcule as tensões de polarização VO1 e VO2.
Figura 2.
1
III
Considere o circuito representado na Figura 3.
a) Calcule as correntes em todos os ramos e as tensões em todos os nós.
b) Em que região de funcionamento(activa, saturação ou corte) se encontra o
transistor?.
c) Projete um divisor de tensão para obter uma tensão na base igual a 3V.
VCC= 10 V
RC=4.7 kΩ
RB1
6V
RE=3.3 kΩ
RB2
Figura 3. Análise de um circuito em dc.
IV
Considere o circuito representado na Figura 4. Ambos os transístores Q1 e Q2 estão a
funcionar na região activa, com VBE=0.7 V. Assuma que β1=50 e β2=100.
Calcule todas as tensões e as correntes nos nós e nos ramos respectivos.
+ 24 V
82 k Ω
1kΩ
Q1
Vo
100 k Ω
Q2
10 kΩ
100 Ω
Figura 4. Circuito de polarização.
2
V
a) Os inventores do primeiro transistor só ficaram convencidos que tinham construído
um dispositivo amplificador quando o ligaram a um pequeno altifalante e puderam
ouvir o som a crepitar. Na emoção do momento, foi a forma mais rápida que
encontraram para saber que a potência do sinal na saída era superior a potência do sinal
na entrada.
Use os seus conhecimentos sobre o funcionamento do transístor bipolar para
mostrar que este dispositivo pode funcionar como um amplificador.
b) Considere o circuito representado na
Figura 5. Com base nos valores das
tensões de polarização diga em que
região (activa, corte ou saturação) se
encontra a funcionar o transístor.
Justifique
VC=6.0 V
VB= 7.0
VE= 6.3
Figura 5.
c) Considere o circuito representado na Figura
6. Assuma que β=100.
Calcule todas as tensões e as correntes nos nós e
nos ramos respectivos.
VCC=+15 V
1k
10 k
200 k
1k
100 k
Figura 6.
10 k
3
VI
Considere o circuito representado na Figura 7.
a) Assuma que o transístor está a funcionar na região activa. Determine todas as tensões
e correntes no circuito.
b) Verifique se o transístor esta na região activa, na região de corte ou em saturação.
Explique as suas conclusões.
RC=3 KΩ
RB=7KΩ
3V
RE=500 Ω
Figura 7.
VII
Considere o circuito representado na Figura 8. Calcule as tensões de polarização, V1,
V2, V3, V4, e V5. Assuma que ambos os transístores tem um β=100.
+10V
+10V
9.1KΩ
V2
V1
5.1KΩ
V5
V3
100KΩ
V4
9.1KΩ
4.3KΩ
-10V
-10V
Figura 8.
4