( ) ˆ

Exercícios de Revisão – Física 3 – Prof. Dr. Cláudio S. Sartori
 WWW.claudio.sartori.nom.br

Link WWW.claudio.sartori.nom.br/fisica3.html
Conteúdo: Extraído de:
Lista parte a
http://www.claudio.sartori.nom.br/lista_fisica3_2bimestre_p_a.pdf
Lista: gabarito parte a.
http://www.claudio.sartori.nom.br/lista_fisica3_2bimestre_p_a_gabarito.pdf
Lista parte b
http://www.claudio.sartori.nom.br/lista_fisica3_2bimestre_p_b.pdf
Lista: gabarito parte b.
http://www.claudio.sartori.nom.br/lista_fisica3_2bimestre_p_b_gabarito.pdf
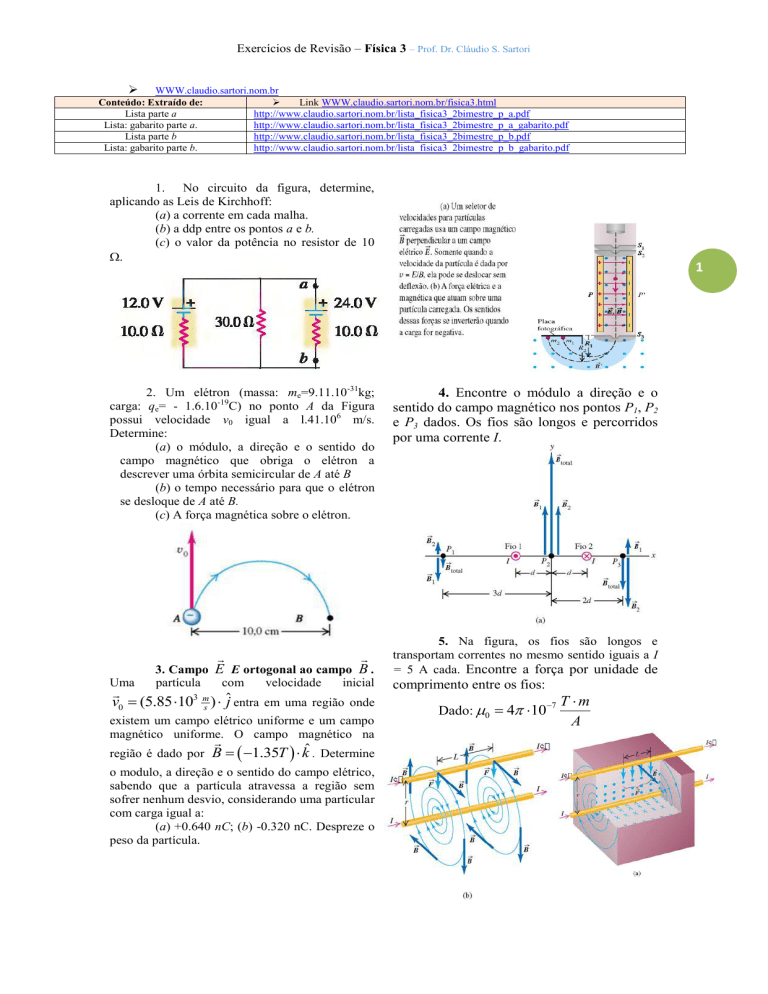
1. No circuito da figura, determine,
aplicando as Leis de Kirchhoff:
(a) a corrente em cada malha.
(b) a ddp entre os pontos a e b.
(c) o valor da potência no resistor de 10
.
2. Um elétron (massa: me=9.11.10-31kg;
carga: qe= - 1.6.10-19C) no ponto A da Figura
possui velocidade v0 igual a l.41.106 m/s.
Determine:
(a) o módulo, a direção e o sentido do
campo magnético que obriga o elétron a
descrever uma órbita semicircular de A até B
(b) o tempo necessário para que o elétron
se desloque de A até B.
(c) A força magnética sobre o elétron.

Uma

3. Campo E E ortogonal ao campo B .
partícula
com
velocidade
inicial

v0  (5.85 103 ms )  ˆj entra em uma região onde
existem um campo elétrico uniforme e um campo
magnético uniforme. O campo magnético na
região é dado por

B   1.35T   kˆ . Determine
o modulo, a direção e o sentido do campo elétrico,
sabendo que a partícula atravessa a região sem
sofrer nenhum desvio, considerando uma partícular
com carga igual a:
(a) +0.640 nC; (b) -0.320 nC. Despreze o
peso da partícula.
1
4. Encontre o módulo a direção e o
sentido do campo magnético nos pontos P1, P2
e P3 dados. Os fios são longos e percorridos
por uma corrente I.
5. Na figura, os fios são longos e
transportam correntes no mesmo sentido iguais a I
= 5 A cada. Encontre a força por unidade de
comprimento entre os fios:
7
Dado: 0  4 10
T m
A
Exercícios de Revisão – Física 3 – Prof. Dr. Cláudio S. Sartori
6. Três fios paralelos condutores têm
correntes de módulo igual a I com os sentidos
indicados na Figura. Sabendo que a distância entre
dois fios adjacentes é igual a d .
Calcule o módulo, a direção e o sentido
da força magnética resultante por unidade de
comprimento sobre o fio 1 e sobre o fio 2. Mostre
que:

FR1
l
 i2 
comprimento 5 cm. A resistência possui valor R =
12 .
0 ˆ
j
4 d
ĵ
2
iˆ
k̂
(a) Determine o valor da indutância da bobina:
L
0  N 2  A
l
 L  0  N 2 
  R2
l
(b) Encontre a constante de tempo do circuito e a
corrente em função do tempo quando a chave for ligada.
L
R

(c) Qual a corrente elétrica após 0.4 ms da chave ser
ligada?
7. Na Figura uma barra condutora ab está
em contato com os trilhos ca e db. O dispositivo
encontra-se em um campo magnético uniforme de
0.800 T perpendicular ao plano da Figura.
(a) Calcule o módulo da tem induzida na
barra quando ela se desloca da esquerda para a
direita com velocidade igual a 7.50 m/s.
(b) Em que sentido a corrente flui na barra ?
(c) Sabendo que a resistência do circuito
abcd é igual a l.50  (suposta constante),
determine o módulo, a direção e o sentido da força
necessária para manter a barra se deslocando da
esquerda para a
direita com velocidade de 7.50 m/s. Despreze o
atrito,
(d) Compare a taxa do trabalho mecânico
realizado pela força magnética (F.v) com a taxa da
energia térmica dissipada no circuito (I2.R).
i(t ) 
 
t
 
 1  e  
R 

(d) Determine o campo magnético sobre o eixo da
bobina nesse instante e o fluxo magnético.
B  0 
N
i    N  B  A
l
(e) Mostre que a densidade de energia ηB
(energia por unidade de volume armazenada pelo
campo magnético no interior da bobina) é dada
B2
por: B 
2 0
Sugestão: Multiplique por i a equação do circuito RL:
L
PL 
di
 R i  
dt
dU m
dt

PR
P


di
2
L i   R i   i
dt
dU m
di
L  i2
 L  i   U m   dU m   L  idi 
dt
dt
2
L
Um 
0  N 2  A B  0  N i  i  l  B
l
0  N
l

L

i2

2

B2  l  A
2  0
Um
B2
 B 
l
A
2  0
V
8. O circuito RL da figura é alimentado
por uma bateria de fem  = 24V e possui uma
bobina de N = 50 voltas, raio R = 3.0 cm e
Calcule esta densidade para o instante de
tempo 0.4 ms.
Exercícios de Revisão – Física 3 – Prof. Dr. Cláudio S. Sartori
9. Em cada caso indicado: Encontre a
direção e o sentido do campo induzido e a corrente
induzida utilizando a Lei de Faraday-Lenz:
Caso
Situação
(a)
(b)
(c)
(d)
Pólo Norte do ímã se afastando da bobina;
Chave S sendo fechada;
Corrente decrescendo no fio.
Barra de cobre movendo-se para direita
enquanto seu eixo é mantido a uma direção
perpendicular a um campo magnético. Se o topo
da barra se torna positivo em relação à parte
inferior, qual a direção do campo magnético?
10. Um circuito R-L-C em série com L =
0.120 H, R = 240  e C = 7.30 F conduz uma
corrente eficaz de 0.450 A com uma freqüência
igual a 400 Hz.
(a) Calcule o ângulo de fase e o fator de
potência do circuito,
(b) Qual é a impedância do circuito ?
(c) Qual é a tensão eficaz da fonte ?
11. Filtros:
(a) Um filtro passa-alto. Uma aplicação
do circuito R-L-C em série consiste no uso de um
filtro passa-alto ou de um filtro passa-baixo, que
filtram, respectivamente, os componentes de baixa
frequência ou os componentes de altas frequências
de um determinado sinal. Um filtro passa-alto é
indicado na Figura 7, onde a tensão de saída é
tomada através da combinação L-R. (A
combinação L-R representa uma bobina de indução
que também possui uma resistência, pois seu
enrolamento é um fio com um comprimento muito
grande.) Deduza uma expressão para Vsaída/Vin,
a razão entre a amplitude da tensão na saída e a
amplitude da tensão da fonte, em função da
frequência angular  da fonte. Mostre que, quando
 é pequeno, essa razão é
proporcional a  e, portanto, é pequena, e mostre
que ela tende a l no limite de freqüências elevadas.
(b) Um filtro passa-baixo. A Figura 8
mostra um filiro passa-baixo (veja o Problema 39);
a tensão de saída é tomada através do capacitor do
circuito R-L-C em série. Deduza uma expressão
para Vsaída/Vin, a razão entre a amplitude da
tensão na saída e a amplitude da tensão da tome,
em função da frequência angular  da fonte.
Mostre que, quando  é grande, essa razão é
proporcional a 2 e, portanto, é muito pequena, e
mostre que ela tende a l no limite de frequências
pequenas.
Vin = m.sen(.t)
3
Exercícios de Revisão – Física 3 – Prof. Dr. Cláudio S. Sartori
12. No circuito RC da figura:
4
A bateria tem fem  = 12.0 V, o resistor
resistência R = 0.8 M (1M= 106) e o capacitor,
capacitância C = 5µF. O capacitor está
descarregado em t = 0s e em seguida, liga-se a
chave iniciando o processo de carga no capacitor.
(a) Encontre a constante de tempo no
circuito   R  C e a equação da carga no
capacitor:
t
 

Q(t )    C 1  e  


(b) Determine a máxima corrente e a
corrente em função do tempo:
i(t ) 

R
e

t

(c) Determine a carga, a corrente, a tensão
no capacitor e a tensão no resistor no instante:
t

2
.
(d) Construa os gráficos: (t,Q(t)) e (t, i(t)).