MRU_MRUV

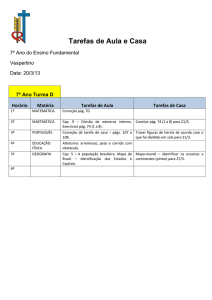
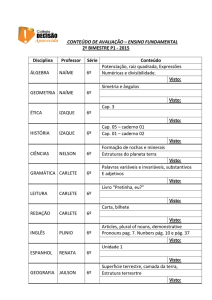
Física I – MRU, MRUV, Queda Livre e Lançamento Vertical
1) (Cap.2, Ex. 64, pág 51, Tipler 5o ed) Um carro esporte BMW-M3 pode ser acelerado, em terceira
marcha, de 48,3 km/h a 80,5 km/h em 3,7 s. a) qual a aceleração média desse carro em m/s 2? b) Se o
carro continuar com essa aceleração por mais um segundo, qual a velocidade com que estará se
movendo?
2) (Cap.2, Ex. 67, pág 51, Tipler 5o ed) A posição de uma certa partícula varia com o tempo de acordo
com a equação
, onde x é expresso em metros e t em segundos. a) determine o
deslocamento e a velocidade média para o intervalo de tempo
s. b) Obtenha a fórmula geral
do deslocamento para o intervalo de tempo que vai de t a t + t. c) Utilize o processo limite para obter a
velocidade instantânea para um tempo t qualquer.
3) (Cap.2, Ex. 69, pág 51, Tipler 5o ed) O movimento unidimensional de uma partícula é mostrado na
figura abaixo. a) qual é a aceleração média nos intervalos AB, BC e CE? b) qual é a distância percorrida
pela partícula 10 s após o início de seu movimento? c) esquematize, em um gráfico, o deslocamento da
partícula em função do tempo; indique os instantes A, B, C, D e E em seu gráfico. d) em que tempo a
partícula está se movendo mais lentamente?
4) (Cap.2, Ex. 70 pág 51, Tipler 5o ed) Um objeto projetado para cima com velocidade inicial vo atinge
uma altura h. Um outro objeto, projetado para cima com velocidade inicial 2 v o, atingirá a altura de: a) 4 h,
b) 3 h, c) 2 h, d) h
5) (Cap.2, Ex. 71 pág 51, Tipler 5o ed) Um carro em repouso na coordenada x = 50 m acelera a uma taxa
constante de 8 m/s2. a) qual é a sua velocidade após 10 s? b) qual é a distância percorrida após 10 s? c)
qual é a sua velocidade média no intervalo 0 ≤ t ≤ 10 s?
6) (Cap.2, Ex. 72 pág 51, Tipler 5o ed) Um corpo com velocidade inicial de 5 m/s possui uma aceleração
constante de 2 m/s2. Quando sua velocidade é de 15 m/s, que distância ele percorreu?
7) (Cap.2, Ex. 75 pág 51, Tipler 5o ed) Uma bola é lançada para cima com uma velocidade inicial de 20
m/s. a) Durante quanto tempo a bola permanece no ar? (despreze a altura do ponto de lançamento). b)
qual é a maior altura atingida pela bola? c) quanto tempo após o lançamento a bola estará 15 m acima do
ponto em eu foi lançada?
8) (Cap.2, Ex. 77 pág 51, Tipler 5o ed) Uma carga de tijolos está sendo elevada por um guindaste com
uma velocidade uniforme de 5 m/s quando um tijolo cai a 6 m acima do solo. a) esquematize o
deslocamento x(t) para mostrar o movimento de queda livre do tijolo. b) qual é a maior altura atingida pelo
tijolo relativamente ao solo? c) Quanto tempo o tijolo gasta para atingir o solo? d) qual é a sua velocidade
no instante imediatamente anterior ao seu impacto com o solo?
9) (Cap.2, Ex. 83 pág 51, Tipler 5o ed) Um ônibus é acelerado a 1,5 m/s2 a partir do repouso por 12 s. Em
seguida, ele se movimenta com velocidade constante por 25 s, após o que diminui a marcha até parar com
uma aceleração de – 1,5 m/s2. a) qual a distância percorrida pelo ônibus? b) Qual a sua velocidade
média?
10) (Cap 2, Ex. 39, pág 35, Halliday 7aed) Em um canteiro de obras, uma chave de cano atinge o solo
com uma velocidade de 24 m/s. a) De que altura deixaram-na cair por descuido? b) quanto tempo durou a
queda? c) Esboce os gráficos de y, v, e de a versus t pra a chave de cano.
11) (Cap 2, Ex. 43, pág 35, Halliday 7aed) Um balão de ar quente está subindo a uma taxa de 12 m/s e
está a 80 m acima do solo quando um pacote é solto por um de seus lados. a) quanto tempo o pacote leva
até atingir o solo? b) com que velocidade ele atinge o solo?
12) (Cap 2, Ex. 47, pág 36, Halliday 7aed) Uma chave cai de uma ponte que está a 45 m acima da água.
Ela cai diretamente sobre um barco, que se move com velocidade constante e estava a 13 m do ponto de
impacto quando a chave foi solta. Qual é a velocidade do barco?
13) (Cap 2, Ex. 58, pág 36, Halliday 7aed) Uma bola é lançada
verticalmente para cima a partir da superfícies de um planeta de um
sistema solar distante. O gráfico de y versus t é mostrado na figura,
onde y é a altura da bola acima de seu ponto de partida e t = 0 no
instante em que a bola é disparada. Quais são os módulos de a)
aceleração de queda livre no planeta e b) da velocidade inicial da bola?
14) (Cap 2, Ex. 21, pág 61, Sears 12a ed) Um antílope que se move com aceleração constante leva 7 s
para percorrer uma distância de 70 m entre dois pontos. Ao passar pelo segundo ponto, sua velocidade é
de 15 m/s.
a) qual era a sua velocidade quando passava pelo primeiro ponto?
b) qual era a sua aceleração?
15) (Cap 2, Ex. 30, pág 62, Sears 12a ed) Para t = 0 um carro pára em um semáforo. Quando a luz fica
verde, o carro começa a acelerar com uma taxa constante, elevando sua velocidade para 20 m/s, 8 s
depois de a luz ficar verde. Ele se move com essa nova velocidade por uma distância de 60 m. A seguir, o
motorista avista uma luz vermelha no cruzamento seguinte e começa a diminuir a velocidade com uma
taca constante. O carro pára no sinal vermelho a 180 m da posição para t = 0. a) para o movimento do
carro, desenhe gráficos acurados de xt, vxt e axt. b) Faça um diagrama do movimento mostrando a
posição, a velocidade e a aceleração do carro.
16) (Cap 2, Ex. 31, pág 62, Sears 12a ed) O gráfico da figura ao lado mostra a
velocidade da motocicleta de um policial em função do tempo. a) calcule a
aceleração instantânea para t = 3 s, t = 7 s e t = 11 s. b) qual foi o
deslocamento do policial nos 5 s iniciais? E nos 9 s iniciais? E nos 13 inicias?
17) (Cap 2, Ex. 42, pág 63, Sears 12a ed) Um tijolo é largado (velocidade
inicial nula) do alto de um edifício. Ele atinge o solo em 2,5 s. A resistência do ar pode ser desprezada, de
modo que o tijolo está em queda livre. a) qual é a altura do edifício? b) qual é o módulo da velocidade
quando ele atinge o solo c) Faça os gráficos ayt, vyt e yt para o movimento do tijolo.
18) (Cap 2, Ex. 44, pág 63, Sears 12a ed) Um balonista de ar quente
que se desloca verticalmente para cima com velocidade constante de
módulo igual a 5 m/s deixa cair um saco de areia no momento em que
ele está a uma distância de 40 m acima do solo. Após ser largado, o
saco de areia passa a se mover em queda livre. A) calcule a posição e a
velocidade do saco de areia 0,25 s e 1 s depois de ser largado. b)
calcule o tempo que o saco de areia leva para atingir o solo desde o
momento em que ele foi lançado, c) qual é a velocidade do saco de
areia quando ele atinge o solo? d) Qual é a altura máxima em relação
ao solo atingida pelo saco de areia? e) faça gráficos a yt, vyt e yt para
movimento do saco de areia.
19) (Cap 2, Ex. 45, pág 63, Sears 12a ed) Um estudante no topo de um edifício joga uma bola com água
verticalmente para baixo. A bola deixa a mão do estudante com uma velocidade de 6 m/s. A resistência do
ar pode ser ignorada e a bola considerada em queda livre após o lançamento. a) calcule sua velocidade
depois de 2 s de queda. b) qual a distância percorrida nesses 2 s? c) qual o módulo da velocidade quando
a bola caiu 10 m? d) faça gráficos ayt, vyt e yt para o movimento.
20) (Cap 2, Ex. 48, pág 64, Sears 12a ed) Uma pedra grande é expelida verticalmente de baixo para cima
por um vulcão com velocidade inicial de 40 m/s. Despreza a resistência do ar. a) qual o tempo que a pedra
leva após o lançamento , para que sua velocidade seja de 20 m/s de baixo para cima? b) Qual o tempo
que a pedra leva, após o lançamento para que sai velocidade seja de 20 m/s de cima para baixo? C)
quando o deslocamento da pedra é igual a zero? d) quando a velocidade da pedra é igual a zero? e) qual
o módulo e o sentido da aceleração enquanto a pedra: i) está se movendo de baixo para cima? ii) estase
movendo de cima para baixo? ii) está no ponto mais elevado da sua trajetória? Faça gráficos a yt, vyt e yt
para o movimento.
21) (Cap 2, Ex. 49, pág 64, Sears 12a ed) Uma rocha de 15 kg cai de uma posição de repouso na Terra e
atinge o solo em 1,75 s. Quando cai da mesma altura no satélite de Saturno, Enceladus, ele atinge o solo
em 18,6 s. Qual é a aceleração da gravidade em Enceladus?
22) (Cap 2, Ex. 76, pág 64, Sears 12a ed) Você está sobre o telhado do prédio de Física, 46 m acima do
solo, como mostra a figura. Seu professor de física, que possui 1,8 m de altura está a caminhando próximo
do edifício com uma velocidade constante de 1,2 m/s. Se você deseja jogar um ovo na cabeça dele, em
que ponto ele deve estar quando você largar o ovo? Suponha que o ovo esteja em queda livre.
23) (Cap 3, Ex. 1, pág 57, Halliday 7aed) Quais são a) a componente x e b) a componente y de um vetor

a no plano xy se ele aponta a 250o no sentido anti-horário em relação ao sentido positivo do eixo x e seu
módulo é 7,3 m?

24) (Cap 3, Ex. 3, pág 57, Halliday 7aed) A componente x de um vetor A é – 25 m e a componente y é +


40 m. a) qual [e o módulo de A ? b) qual é o ângulo entre o sentido de A e o sentido positivo de x?

25) (Cap 3, Ex. 4, pág 57, Halliday 7aed) Um vetor deslocamento r no
plano xy tem módulo de 15 m e o sentido especificado pelo ângulo
  30 o , como mostra a figura. Determine a) a componente x e b) a
componente y do vetor.
 
26) (Cap 3, Ex. 11, pág 58, Halliday 7aed) Em termos de vetores unitários, qual é a soma a  b se

^

^
^
 
^
a  (4,0m) i  (3,0m) j e b  (213 ,0m) i  (7,0m) j ? Quais são: b) o módulo e c) o sentido de a  b ?
27) (Cap 3, Ex. 15, pág 58, Halliday 7aed) Dois vetores são dados por:

^
^
^
a  (4,0m) i  (3,0m) j  (1,0m) k

^
^
e
^
b  (1,0m) i  (1,0m) j  (4,0m) k
 
 




Em termos de vetores unitários, encontre a) a  b , b) a  b e c) um terceiro vetor c tal que a  b  c  0 .