Apostila 4 MAT 1 - FUNÇÃO MODULAR

=8.10.
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 FUNÇÃO MODULAR
8.10.1. FUNÇÃO DEFINIDA POR MAIS DE UMA SENTENÇA
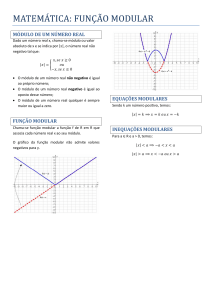
EXEMPLO 1:
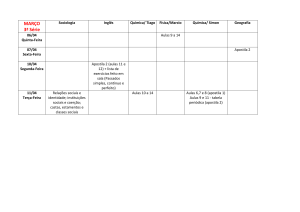
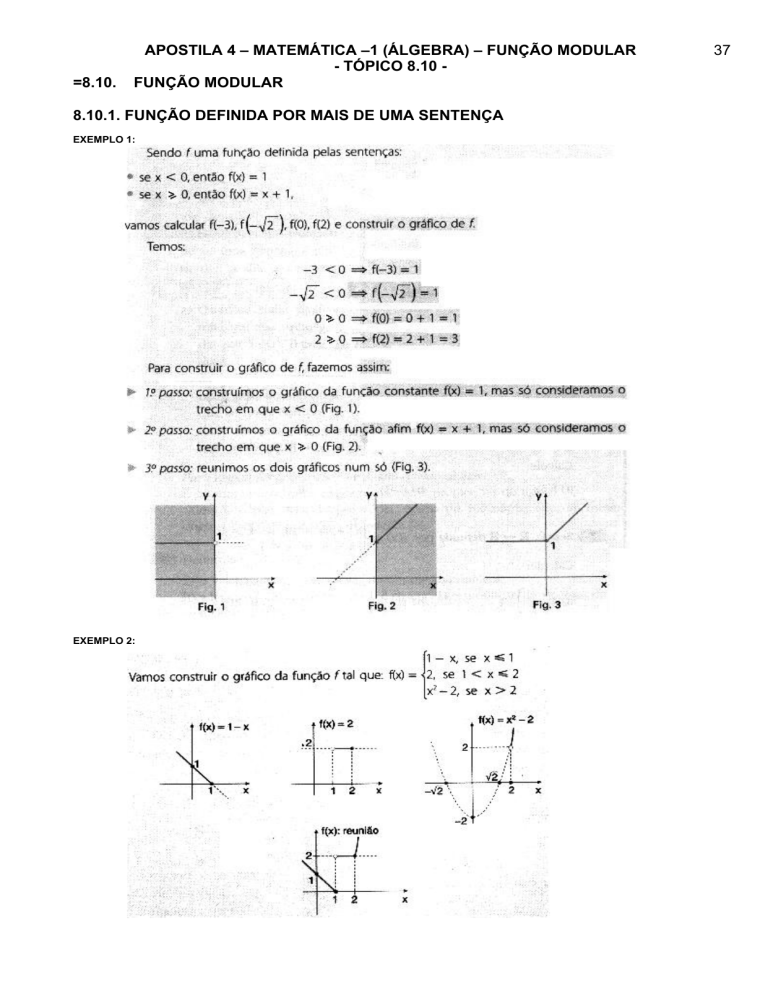
EXEMPLO 2:
37
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 8.10.2. MÓDULO DE UM NÚMERO REAL
Dado um número real x, chama-se módulo ou valor absoluto de x, e indica-se com | x | , o
número real não negativo tal que:
 | x |  x , se x  0

ou

| x |   x , se x  0

 | 4 | 4

Exemplos:  | 0 |  0
 |  7 | 7

Observação:
x 2 | x | , assim, a informação
( 1) 2  1 É FALSA!
8.10.3. DEFINIÇÃO DA FUNÇÃO MODULAR
Chama-se função modular a função de IR em IR dada pela lei f ( x ) | x | .
 x , se x  0
f ( x ) | x |  f ( x )  
  x , se x  0
8.10.4. GRÁFICO DA FUNÇÃO MODULAR
38
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 8.10.5. GRÁFICOS DE FUNÇÕES EM MÓDULO
Exemplo 1: f ( x ) | x  1 |
Exemplo 2: f ( x ) | x 2  4 |

39
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 -
40
Exemplo 3: h( x ) | x | 1
Obs.: Uma maneira prática para deslocarmos o gráfico do exemplo anterior é, na fig 1, deslocarmos o eixo
das abscissas para cima uma unidade.
Exemplo 4: f ( x )  ( x  3 ) 2
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 Exemplo 5: f ( x ) | x  1 |  | x  1 |
1º passo: fazer f ( x )  g( x )  h( x ) ;
2º passo: analisar o comportamento algébrico de g(x) e de h(x) individualmente, ou seja:
 x  1, se x  1
 x  1, se x  1
g( x )  | x  1 |  
e h ( x ) | x  1 |  
  x  1, se x  1
  x  1, se x  1
3º passo:
  2 x , se x  1

Assim, f ( x ) | x  1 |  | x  1 |   2, se  1  x  1
 2 x , se x  1

Exemplo 6: Construa o gráfico de f ( x )  2  | x |  | x  1 | e determine suas raízes.
Analogamente ao exemplo anterior, temos:
Do gráfico vemos que há duas raízes,
 A primeira é  1 ;
 A segunda está entre 0 e 1. De fato, se
1
3x 1 0  x  .
3
41
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 Exemplo 7: f ( x ) | | 2 x  3 |  2 |
42
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 -
EXERCÍCIOS:
1) Construir o gráfico da função f ( x )  | x  1 | 2 .
RESPOSTA:
2) Construir o gráfico da função f ( x ) | x 2  4 x | e
determinar o seu domínio e conjunto imagem.
RESPOSTA:
3) Construir o gráfico da função
RESPOSTA:
f ( x ) | x 2  4 x  3 | 2 e determinar seu domínio
e conjunto imagem.
4) Determine o conjunto imagem da função
f ( x ) | x  2 | definida no intervalo real [1, 3 ] .
RESPOSTA:
{ y  IR | 1  x  3 }
43
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 -
44
8.11. EQUAÇÕES MODULARES NA VARIÁVEL x
Basicamente existem quatro tipos de equações modulares:
TIPO 1:
(exp ressão em x )  n º real
Exemplo: | x  1 |  2 .
 x 1 2  x  3

| x 1| 2  
ou
 x  1  2  x  1

S  {  1 ;3 }
TIPO 2:
(exp ressão em x )  k  ( outra exp ressão em x ) , onde k  IR.
Exemplo: | x  2 |  2 | x  2 | .

 x  2  2  ( x  2)  x  6

| x  2 |  2 | x  2 |  
ou
2

 x  2  2  (  x  2 )  x  3
20
S{6;
}
3
TIPO 3:
(exp ressão em x )  (outra expressão em x).
Atenção, observe que temos uma expressão em x no segundo membro da equação
representando o resultado do módulo presente no primeiro membro; sabemos que o resultado
de um módulo não pode ser negativo.
Assim, para este tipo de equação modular, deveremos iniciar sua resolução impondo a
condição de existência do módulo em questão, vejamos o exemplo abaixo:
Exemplo: | 3 x  5 |  5 x  1.

Condição de existência do módulo: 5 x  1  0  x 

Resolvendo a equação:

 3x  5  5x 1 x   2

| 3x  5 |5x 1  
ou
3

 3 x  5   5 x  1  x  4

3 
Verificando na condição de existência: S   
4
1
5
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
- TÓPICO 8.10 -
TIPO 4: A equação apresenta
Exemplo: x
2
x
2
45
.
 2 x 8  0
Para resolvermos este tipo de equação deveremos fazer x  y .
Assim, y 2  2  y  8  0.
 y4

y  2  y  8  0   ou
 y  2

Efetuando o retorno à variável x:
2
x 4
x4
ou
Resposta: S  {  4 ; 4 }
x  2
x  IR
x  4
Nota: Existem basicamente estes quatro tipos de equações modulares, entretanto, é
necessário estar atento às diversas combinações de equações geradas a partir
destes tipos.
Exemplo: Resolva, em IR, a equação 2 | x  1 | 2  3 | x  1 |  2  0 .
Resolução:
Resposta: S    1; 3
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – INEQUAÇÕES MODULARES
- TÓPICO 8.12
46
8.12. INEQUAÇÕES MODULARES
Sendo “EEX” uma expressão em x e “k” um número real positivo, de modo geral temos dois
casos de inequações modulares:
CASO 1: EEX  k
CASO 2: EEX  k
EEX   k

 ou
 EEX  k

 k  EEX  k
Exemplo-2: Resolva x  2  5 .
Exemplo-1: Resolva x  1  2 .
 2  x 1 2
1 x  3
S    1, 3

 x  2  5  x  3

ou

x25  x 7

S   x  IR | x  3 ou x  7 
Obs.: Os casos 1 e 2 também se verificam, respectivamente, para as situações de "  " e "  ".
Exemplo 3: Resolva, em IR, a inequação | 2 x  1 |  x  1 .
Neste exemplo temos, no segundo membro, outra expressão em x; assim, teremos que
analisar duas situações:
1

 2 x  1, se x  2 ( I )
Como sabemos que | 2 x  1 |  
  2 x  1, se x  1 ( II )

2
1
(a) e 2 x  1  x  1  x  2 (b)
Em ( I ): x 
2
Então teremos ( a )  ( b )  S 1  x  IR | x  2 }
Em ( II ): x 
1
(c) e  2 x  1  x  1 
2
x  0 (d)
Então teremos ( c )  ( d )  S 2  x  IR | x  0 }
Logo, a solução da inequação dada é:
S S
1
2
 x  IR | x  0 ou x  2 }
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – INEQUAÇÕES MODULARES
- TÓPICO 8.12
EXERCÍCIOS
1)
Resolva, em IR, a inequação 2 x  1  3 .
2)
Resolva, em IR, a inequação x  4  1.
3)
Resolva a inequação x
4)
5)
Resolva a inequação
2
 4 x  3  0 , em IR.
x4
 0 , em IR.
x 1
Determine o domínio D da função f ( x ) 
47
Resposta:
S  { x  IR | x  1 ou x  2 }
Resposta:
S  { x  IR | 3  x  5 }
Resposta:
S  { x  IR |  1  x  1 ou x  3 ou x  3 }
Resposta:
S  { x  IR | x  4 e x  1 }
1
2x  5  3
.
Resposta:
D  { x  IR | x  1 ou x  4 }
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
TESTES COMPLEMENTARES
1)
Resposta:A
2)
Resposta:C
3)
Resposta B
4)
Resposta A
5)
Resposta: D
48
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
6)
Resposta: B
7)
Resposta: B
8)
Resposta: C
9)
Resposta: C
10)
Resposta: C
11)
Resposta: B
49
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
12)
Resposta: A
13)
Resposta: B
14)
Resposta: A
15)
Resposta: C
16)
Resposta: A
17)
Resposta: B
50
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
18)
Resposta: D
19)
Resposta: E
20)
Resposta: C
51
APOSTILA 4 – MATEMÁTICA –1 (ÁLGEBRA) – FUNÇÃO MODULAR
QUESTÕES DISCURSIVAS
D1)
Respostas:
a)
b)
Somente para x  
c)
x
5
7
e x
4
2
D2)
a)
b)
c)
Respostas:
-1, 0 e 1
7
6
52