arquivo

Gráficos (UM e UMV)
Gabarito:
Resposta da questão 1:
[E]
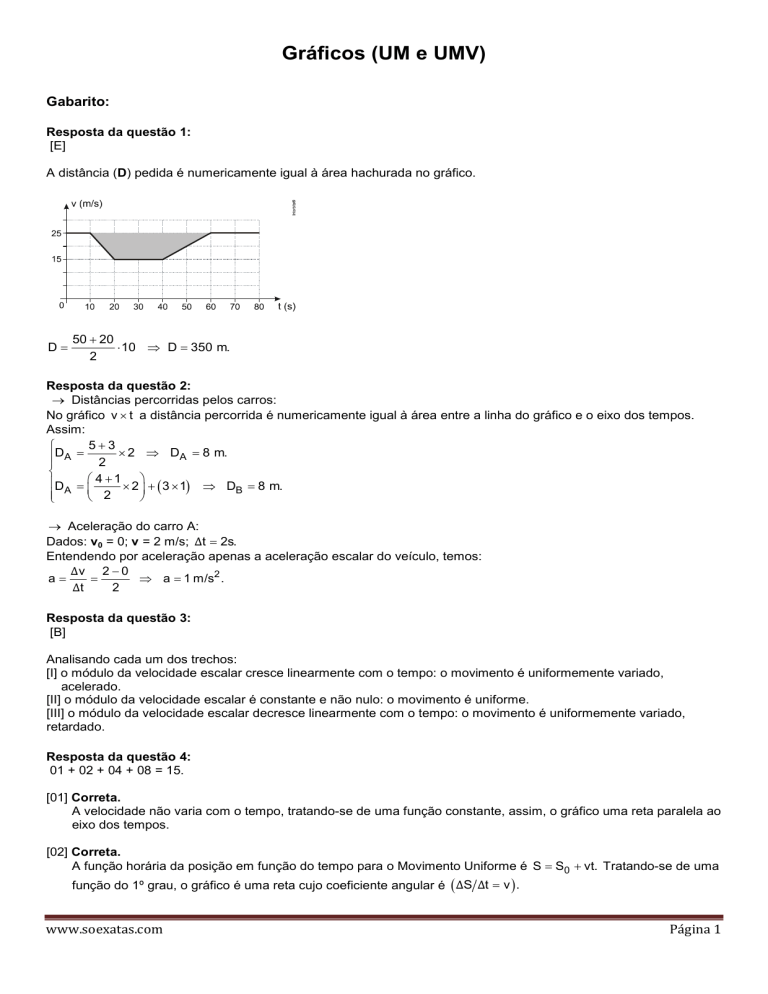
A distância (D) pedida é numericamente igual à área hachurada no gráfico.
D=
50 + 20
⋅ 10 ⇒ D = 350 m.
2
Resposta da questão 2:
→ Distâncias percorridas pelos carros:
No gráfico v × t a distância percorrida é numericamente igual à área entre a linha do gráfico e o eixo dos tempos.
Assim:
5+3

DA = 2 × 2 ⇒ DA = 8 m.


D =  4 + 1 × 2  + ( 3 × 1) ⇒ D = 8 m.
B

 A  2

→ Aceleração do carro A:
Dados: v0 = 0; v = 2 m/s; Δt = 2s.
Entendendo por aceleração apenas a aceleração escalar do veículo, temos:
Δv 2 − 0
a=
=
⇒ a = 1 m/s2 .
Δt
2
Resposta da questão 3:
[B]
Analisando cada um dos trechos:
[I] o módulo da velocidade escalar cresce linearmente com o tempo: o movimento é uniformemente variado,
acelerado.
[II] o módulo da velocidade escalar é constante e não nulo: o movimento é uniforme.
[III] o módulo da velocidade escalar decresce linearmente com o tempo: o movimento é uniformemente variado,
retardado.
Resposta da questão 4:
01 + 02 + 04 + 08 = 15.
[01] Correta.
A velocidade não varia com o tempo, tratando-se de uma função constante, assim, o gráfico uma reta paralela ao
eixo dos tempos.
[02] Correta.
A função horária da posição em função do tempo para o Movimento Uniforme é S = S0 + vt. Tratando-se de uma
função do 1º grau, o gráfico é uma reta cujo coeficiente angular é ( ΔS Δt = v ) .
www.soexatas.com
Página 1
[04] Correta.
A função horária do espaço percorrido em função do tempo para o Movimento Uniforme é ΔS = vt. Tratando-se
de uma função do 1º grau, o gráfico é uma reta.
[08] Correta.
No gráfico v × t, a “área” entre a linha do gráfico e o eixo dos tempos dá o espaço percorrido.
[16] Incorreta.
No Movimento Uniformemente Variado, a função horária da velocidade é v = v 0 + at. Como é uma função do 1º grau,
o gráfico da velocidade em função do tempo é uma reta.
Resposta da questão 5:
[B]
Para calcular o deslocamento do jipe-robô, usamos a propriedade do gráfico v × t, calculando a “área” destacada no
gráfico abaixo.
ΔS =
20 + 15
15 + 10
10 + 7,5
10 + 5
5⋅5
⋅ 15 +
⋅ 5 + 10 ⋅ 10 + 2 ⋅
⋅5 +
⋅ 10 +
⇒
2
2
2
2
2
ΔS = 262,5 + 62,5 + 100 + 87,5 + 75 + 12,5 = 600 cm ⇒
ΔS = 6 m.
Resposta da questão 6:
Calculando o deslocamento ( Δx A ) do móvel A até o instante t = 15 s.
Da propriedade do gráfico v × t.
15 + 10
∆x A = "área" =
⋅ 10 ⇒ ∆x A = 25 ⋅ 5 ⇒
2
∆x A = 125 m.
Calculando o instante em que a distância entre os móveis é igual a 332 m, usando novamente a propriedade anterior:
www.soexatas.com
Página 2
Δx A =
t + (t − 5)
2
= (2 t − 5) 5
⇒ Δx A = 10 t − 25.
Sendo x0A = 0, temos:
x A = x0A + Δx A = 0 + 10 t − 25 ⇒ x A = 10 t − 25 .
 t + (t − 8) 
= − ( 2 t − 8 ) 5 ⇒ ΔxB = −10 t + 40.
Δ xB = − 


2


Sendo x0B = 3 m, temos:
xB = x0B + Δx A = 3 − 10 t + 40 ⇒ xB = −10 t + 43.
No instante t a distância entre os móveis (DAB ) deve ser 332 m.
DAB = x A − xB ⇒ 332 = 10 t − 25 − ( −10 t + 43 ) ⇒ 332 = 20 t − 68 ⇒ 20 t = 400
⇒
t = 20 s.
Resposta da questão 7:
[A]
[A] Verdadeira. Os gráficos apresentados são de deslocamento por tempo. Como o enunciado nos informa que o
automóvel desenvolve velocidade constante de módulo v, no início e no final, teremos a função d = v.t de primeiro
grau, ou seja, o gráfico deverá ser uma reta no inicio e no final o que é satisfeito por todas as alternativas.
No intervalo Δt o automóvel aumenta e em seguida diminui sua velocidade, ambos uniformemente, o que nos
a.t 2
de segundo grau, ou seja, o gráfico deverá ser duas parábolas seguidas, a primeira
2
com concavidade para cima, o que representa o aumento da velocidade e a segunda com a concavidade para
baixo, o que representa a diminuição da velocidade, sendo a alternativa [A] a única que satisfaz o enunciado.
remete à função d = v.t +
[B] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[C] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[D] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[E] Falsa. O gráfico apresenta, aparentemente, duas parábolas, porém com as concavidades invertidas.
Resposta da questão 8:
[D]
A “área” no diagrama v×t é numericamente igual ao espaço percorrido (d).
Dividimos a figura em 2 partes e calculamos a “área” da seguinte forma:
d = A1 ( trapézio ) + A 2 ( retângulo ) = (10 + 2) × 1/2 + 10 × 1 = 6 + 10 = 16 km.
Mas o tempo total gasto é t = 2 h.
Então a velocidade média é:
vm = d/t = 16/2 = 8 km/h.
Resposta da questão 9:
www.soexatas.com
Página 3
[C]
As áreas da figura abaixo representam o deslocamento. Como uma é positiva e a outra negativa de mesmo módulo,
o deslocamento total é nulo.
Resposta da questão 10:
[D]
O enunciado nos informa que o movimento é uniformemente
acelerado e retrógrado. Com isso, podemos concluir que:
– sua velocidade possui um sinal negativo por estar se deslocando
contra a orientação da trajetória (movimento retrógrado);
– sua aceleração é constante com sinal igual ao da velocidade, ou
seja, negativo (movimento uniformemente acelerado).
[A] Falsa. Aparentemente temos uma parábola em um gráfico de
espaço (S) por tempo (t), voltada para cima, ou seja, é um gráfico
de movimento uniformemente variado (parábola em Sxt) com
aceleração positiva (voltada para cima).
[B] Falsa. Temos uma reta em um gráfico de espaço por tempo, o que representa um movimento uniforme, ou seja,
com velocidade constante e aceleração igual a zero.
[C] Falsa. Temos uma reta em um gráfico de velocidade por tempo, o que representa um movimento uniformemente
variado, porém com uma inclinação que representa uma aceleração positiva.
[D] Verdadeira. Temos uma reta em um gráfico de aceleração por tempo, que nos informa que a aceleração é
constante e negativa, conforme o enunciado.
Resposta da questão 11:
[C]
O enunciado nos pede a relação entre os deslocamentos BC e AB, ou seja:
∆SBC
= ?.
∆SAB
Lembrando que o valor da área da figura de um gráfico Vxt é igual à intensidade do deslocamento do corpo, teremos:
Área 1 = ∆SAB , que ocorreu entre 0 e t1.
Área 1 = ∆S AB = b.h = (t1 − 0).(V0 − 0) = t1.V0
Área 2 = ∆SBC , que ocorreu entre t1e t2.
www.soexatas.com
Página 4
Área 2 = ∆SBC =
∆SBC
=
∆SAB
b.h (t 2 − t1 ).(V0 − 0) (t 2 − t1 ).V0
=
=
2
2
2
(t 2 − t1 ).V0
(t − t ).V
t −t
1
2
= 2 1 0.
= 2 1
t1.V0
2
t1.V0
2.t1
Resposta da questão 12:
[D]
Considerando que os carros B e P iniciem seus movimentos no mesmo espaço e no mesmo instante t0 (instante em
que o carro B passa pelos policiais e a perseguição se inicia), eles irão se encontrar novamente quando percorrerem
o mesmo deslocamento no mesmo intervalo de tempo, ou seja: ∆SB = ∆SP e ∆tB = ∆tP .
Conseguiremos encontrar o deslocamento de cada carro através da área do gráfico, já que o gráfico dado é de
velocidade em função do tempo.
Analisando o gráfico dado, concluímos que as áreas serão iguais em t4:
Resposta da questão 13:
[C]
1º Trecho: movimento acelerado (a > 0) → o gráfico da posição em função do tempo é uma curva de concavidade
para cima.
2º Trecho: movimento uniforme (a = 0) → o gráfico da posição em função do tempo é um segmento de reta
crescente.
3º Trecho: movimento desacelerado (a < 0) → o gráfico da posição em função do tempo é uma curva de
concavidade para baixo.
Resposta da questão 14:
[A]
No gráfico da velocidade em função do tempo, a “área” (A) entre a linha do gráfico e o eixo t dá o deslocamento
escalar.
ΔS = ΔS0→1 + ΔS1→2 =
1( 40 )
2
+
1( −40 )
2
= 20 − 20 ⇒
ΔS = 0.
www.soexatas.com
Página 5
Resposta da questão 15:
[A]
Construindo o gráfico:
Resposta da questão 16:
[D]
A área da figura sombreada é numericamente igual ao deslocamento.
ΔS = 30 + 60 + 27 = 117km .
Vm =
ΔS 117
117
=
km / h =
m / s = 6,5m / s .
Δt
5
5x3,6
Resposta da questão 17:
[E]
No trecho I, a declividade da curva espaço-tempo está aumentando, portanto o módulo da velocidade está
aumentando, logo o movimento é acelerado.
No trecho II, o espaço é constante, portanto o móvel está em repouso.
No trecho III, o espaço diminui linearmente com o tempo, tratando-se de um movimento uniforme retrógrado.
Resposta da questão 18:
[B]
Note que entre 3 e 8 min a posição não varia. Portanto, o carro está parado.
Resposta da questão 19:
[C]
www.soexatas.com
Página 6
Pela leitura do gráfico, conclui-se que o objeto atinge a superfície do lago no instante t = 1 s, com velocidade de 10
m/s, pois a partir desse instante sua velocidade começa a diminuir, chegando ao fundo do lago no instante t = 3,5 s,
quando a velocidade se anula.
A profundidade do lago (h2) pode ser calculada pela “área” (A2) da figura abaixo da linha do gráfico entre t = 1 s a t =
3,5 s.
h2 = " A 2 " =
1× 9
+ ( 3,5 − 1) × 1 = 4,5 + 2,5 ⇒
2
h2 = 7 m.
Resposta da questão 20:
[B]
Como o movimento é retilíneo, a aceleração tem módulo igual ao módulo da aceleração escalar, dado por:
| a |=
| ∆v |
. Assim:
∆t
aI = aII (constante) ≠ 0; aIII = 0; aIV ≠ 0 (constante)
Resposta da questão 21:
[D]
Propriedade do gráfico v = f(t): a área entre a linha do gráfico e o eixo t representa o espaço percorrido pelo móvel
(∆
∆S). Como não há mudança de sentido, o espaço percorrido é igual à distância percorrida.
Resposta da questão 22:
[C]
Analisando o gráfico:
No instante t = 30 min, Tânia está passando pelo km 12, onde fica a igreja. Ângela passa por esse marco no instante
t = 40 min, isto é, 10 min após o telefonema. No instante t = 40 min, Tânia está no km 16, ou seja, 4 km à frente de
Ângela.
www.soexatas.com
Página 7
Resposta da questão 23:
[B]
Analisemos cada intervalo:
– De 0 a 3 s: o movimento é uniformemente acelerado; a aceleração escalar é
a1 =
∆v 1 8
2
= ≅ 2,7 m/s .
∆t1 3
O espaço percorrido é calculado pela “área” de 0 a 3 s
3×8
∆S1 =
= 12 m.
2
– De 3 s a 5 s: o movimento é uniforme, com velocidade escalar v2 = 8 m/s.
O espaço percorrido é:
∆S2 = v2 ∆t2 ⇒ 8 × 2 = 16 m.
– De 5 s s 7 s: o movimento é uniformemente retardado; a aceleração escalar é:
a3 =
∆v 3 0 − 8 − 8
2
=
=
= −4 m/s .
∆t 3 7 − 5
2
O espaço percorrido é:
2×8
∆S 3 =
= 8 m.
2
Resposta da questão 24:
[B]
O gráfico sugere: movimento progressivo acelerado (corrida para pegar o ônibus); repouso (espera no ponto);
movimento uniforme regressivo (volta para casa); novo repouso (espera pelo táxi) e, finalmente, movimento
progressivo uniforme (movimento do táxi).
Resposta da questão 25:
[A]
No gráfico, a distância percorrida é: d = OA + AB + BC
(AO)2 = 6 2 + 82 = 100 ⇒ AO = 10 cm ;
AB = (12 − 6) = 6 cm ;
BC = (8 − 0) = 8 cm ;
www.soexatas.com
Página 8
Assim: d = 10 + 6 + 8 = 24 cm.
2
Obedecendo à escala dada, d = 24 ×1.000 = 24.000 cm = 240 m = 2,4 × 10 m.
No gráfico, o deslocamento (vetorial) é: D = | OC | = 12 cm, no sentido de O para C.
2
Obedecendo à escala dada: D = 12 × 1.000 = 12.000 cm = 120 m = 1,2 × 10 m.
Resposta da questão 26:
[C]
No intervalo de 0 a 1 h, a velocidade escalar é positiva e tem módulo decrescente. Então, o movimento é progressivo
e desacelerado.
No intervalo de 1 h a 2 h, a velocidade escalar é negativa e tem módulo crescente. Então, o movimento é regressivo
(ou retrógrado) e acelerado.
Resposta da questão 27:
A rigor, o problema não tem solução, pois os dados da tabela não são suficientes para se chegar a alguma
conclusão. Qualquer curva passando pelos pontos tabelados é uma solução. Para se chegar à resposta esperada, o
examinador deveria informar que a taxa de variação da velocidade entre dois instantes consecutivos mostrados na
tabela é constante.
a) Com “muito boa vontade” vamos à resolução com os valores sugeridos e não dados pela tabela (resposta
esperada pelo examinador), supondo que nos intervalos de 0 e 4 s e de 12 s a 16 s a velocidade permaneça
constante e que, nos intervalos de 4 s a 8 s e de 16 s a 20 s as variações de velocidade sejam constantes. Com
essas considerações, o gráfico pedido está representado a seguir.
b) Com base no gráfico obtido no item a) podemos descrever o movimento do carrinho da seguinte maneira:
de t = 0 a t = 4 s o movimento é progressivo e uniforme;
de t = 4 s a t = 8 s o movimento é progressivo e uniformemente retardado;
de t = 8 s a t = 12 s o movimento é retrógrado e uniformemente acelerado;
de t = 12 s a t = 16 s o movimento é retrógrado e uniforme,
de t = 16 s a t = 20 s o movimento é retrógrado e uniformemente retardado.
Resposta da questão 28:
[A]
É um gráfico de aceleração × tempo. Analisando-o podemos afirmar que a aceleração é constante e não nula nos
intervalos C e G e nula no intervalo E, sendo assim, constante a velocidade.
Resposta da questão 29:
[D]
Pelo gráfico, percebe-se que o motorista imprudente é o condutor do veículo A, que recebe acelerações e
desacelerações mais bruscas.
www.soexatas.com
Página 9
30 − 10 20
2
=
⇒ |a(I)| = 2,0 m/s .
20 − 10 10
0 − 30
−30
2
⇒ a(II) = 3,0 m/s .
De 30 s a 40 s: a(II) =
=
40 − 30
10
De 10 s a 20 s: |a(I)| =
Resposta da questão 30:
[D]
Durante a subida, agem na bolha o empuxo ( E ) e o peso ( P ), uma vez que as forças resistivas são desprezíveis.
Se, conforme supõe o enunciado, as bolhas têm o mesmo tamanho (ou mesmo volume) e a mesma quantidade de
gás, o empuxo e o peso são constantes.
Se uma bolha sobe em movimento acelerado, então E > P.
Aplicando o princípio fundamental da dinâmica:
Fres = E – P = m a.
Se E e P são constantes, a resultante é constante, logo a aceleração também é constante. Isso significa que o
movimento é uniformemente acelerado. Como a bolha parte do repouso, a velocidade inicial é nula, portanto a função
horária da velocidade é:
v = at. O gráfico da velocidade em função do tempo é uma reta, o que nos leva ao gráfico VI.
A função horária do espaço (S) para um movimento uniformemente variado, a partir do repouso, supondo posição
inicial nula é:
1
S = a t 2 . O gráfico correspondente é um arco de parábola que passa pela origem, o que nos remete ao gráfico II.
2
Resposta da questão 31:
[C]
Como a trajetória é retilínea, a aceleração restringe-se à componente tangencial ( a t ), que, em módulo, é igual a
aceleração escalar (a), dada pela taxa de variação da velocidade (∆
∆v) em relação ao tempo (∆
∆t).
a=
∆v
. Usando essa expressão em cada um dos intervalos:
∆t
I. aI =
40 − 0
4−0
2
⇒ aI = 10 m/s .
II. aII = 0 (não houve variação da velocidade)
III. aIII =
0 − 40 −40
2
=
⇒ aIII = – 5 m/s .
14 − 6
8
Resposta da questão 32:
[B]
Como o gráfico da velocidade em função do tempo é uma reta, trata-se de movimento uniformemente variado.
Desses gráficos podemos tirar que:
S0 = 0; v0 = 10 m/s.
www.soexatas.com
Página 10
Podemos ainda concluir que no instante t = 2 s a velocidade se anula (v = 0), ou seja, o móvel inverte o sentido de
seu movimento, uma vez que a trajetória é retilínea.
Calculando o espaço percorrido de 0 a 2 s pela “área” no primeiro gráfico:
∆S =
2 × 10
= 10 m.
2
Mas:
∆S = S – S0 ⇒ 10 = S – 20 ⇒ S = 30 m.
Resposta da questão 33:
Lembrando que no gráfico da aceleração escalar em função do tempo a variação da velocidade é numericamente
igual a área entre a linha do gráfico e o eixo dos tempos, como destacado na figura, temos:
∆v = ∆v1 + ∆v2 + ∆v3 = ∆v = (6 × 4) – (4 × 3) + (6 × 4) = 24 –12 + 24 = 36 cm/s.
Mas ∆v = v – v0. Então:
v – 2 = 36 ⇒
v = 38 cm/s.
Resposta da questão 34:
[D]
As áreas das figuras sombreadas são numericamente iguais aos deslocamentos dos corpos.
∆S1 =
10 × 5
= 25m → o corpo 1 está a 25m da posição inicial
2
10 × 5
= 25m → o corpo 2 está a 25m da posição inicial
2
50
7.
− 20
t.5 (10 − t).2 5t + 2t − 20 7t − 20
7
∆S3 =
−
=
=
=
= 15m
2
2
2
2
2
∆S 2 =
→ o corpo 3 está a 15m da posição inicial
∆S4 = 10.( −2) = −20m → o corpo 2 está a 20m da posição inicial
Resposta da questão 35:
[A]
Nos intervalos de tempo em que a velocidade escalar é constante (1 s a
2 s; 3 s a 4 s e 5 s a 6 s) a aceleração escalar é nula. Nos intervalos 0 a
1 s; 2 s a 3 s; 4 s a 5 s e 6 s a 7 s, a velocidade varia linearmente com o
tempo, sendo, então, a aceleração escalar constante.
∆v
. Assim:
Podemos, então, fazer a =
∆t
www.soexatas.com
Página 11
1− 0
= 1 m / s2 ;
1− 0
4 −1
2
De 2 s a 3 s: a =
= 3 m/s ;
3−2
−1 − 4
2
De 4 s a 5 s: a =
= −5 m/s ;
5−4
0 − ( −1)
2
= 1 m/s .
De 6 s a 7 s: a =
7−6
De 0 a 1 s: a =
Resposta da questão 36:
[A]
Antes do instante t1 , os veículos apresentam a mesma velocidade em relação ao solo e, desta forma, apresentam
velocidade relativa nula. Isto pode ser observado em todas as alternativas. Entre o instante t1 e t 2 apenas o carro de
Felipe está acelerado e, deste modo, a distância entre os carros aumenta, o que significa que a velocidade relativa
aumenta. Como este aumento é linear, visto que a aceleração é constante, neste intervalo entre t1 e t 2 , a linha de
gráfico deverá ser retilínea e crescente. Isto pode ser visto nas opções A e B.
A partir do instante t 2 , a velocidade do carro de Barrichelo começa a crescer no mesmo ritmo da de Felipe, de modo
que a velocidade relativa se fixa novamente. Desta forma, a alternativa correta é a A.
Resposta da questão 37:
O gráfico solicitado entre t = 0 e t = 10 s.
2
Se x = 5 + 16.t – 2.t então v = 16 – 4.t
→ v = 16 – 4.4 = 16 – 16 = 0 m/s
Em t = 0 s → S = 5 m e em t = 5 s → S = 5 + 16.5 – 2.(5) = 5 + 80 – 50 = 35 m. Desta forma como a
2
partícula avança até a posição máxima em t = 4 s → S = 5 + 16.4 – 2.(4) = 5 + 64 – 32 = 37 m, a distância
percorrida é (37 – 5) + (37 – 35) = 32 + 2 = 34 m. O deslocamento é 35 – 5 = 30 m.
2
Resposta da questão 38:
[E]
Resolução
Entre os instantes 1 e 2 a velocidade é negativa e desta forma a partícula viaja no sentido negativo do eixo.
No instante 2 a partícula muda o sinal de sua velocidade e consequentemente muda o sentido de seu movimento.
Para isto precisa, ainda que momentaneamente entrar em repouso, visto que seu movimento é unidimensional.
A área entre a linha de gráfico e o eixo do tempo neste diagrama também, como a função horária, determina o
deslocamento da partícula.
Resposta da questão 39:
[C]
www.soexatas.com
Página 12
Resolução
1
m/s.
2
1
A velocidade é numericamente igual a tangente de alfa → tgα =
= 0,5
2
2
A velocidade do gráfico 2 será numericamente igual a tg(2α), que é → tg(2α) = 2.tgα / (1 – tg α) = 2.0,5 / (1 – 0,25)
1
1 4
=
= =
3
0,75
3
4
Pela equação horária do gráfico 1 a velocidade constante é
Resposta da questão 40:
a) Observe o gráfico
É interessante notar que como o movimento é caracterizado por duas acelerações, uma de 0 a 20 s e outra de 20 s a
50 s, o diagrama da velocidade manterá esta característica com uma velocidade crescente no primeiro trecho (pois a
aceleração é positiva) e uma velocidade decrescente no segundo trecho.
b) A distância percorrida é 1150m.
Este mesmo diagrama pode nos fornecer a distância percorrida, pois esta é numericamente a área entre a linha de
gráfico e o eixo das abscissas. Assim: ∆S = 20.40/2 + (10 + 40).(50 - 20) / 2 = 800/2 + 1500/2 = 400 + 750 = 1150 m
www.soexatas.com
Página 13