resistência dos materiais i

UNIVERSIDADE FEDERAL DE GOIÁS
ESCOLA DE ENGENHARIA CIVIL
RESISTÊNCIA DOS MATERIAIS I
PRIMEIRA PROVA
Duração: 3 hr 00 min.
Data: 11/10/2014
Escolha 4 questões
NOME:
Matrícula:
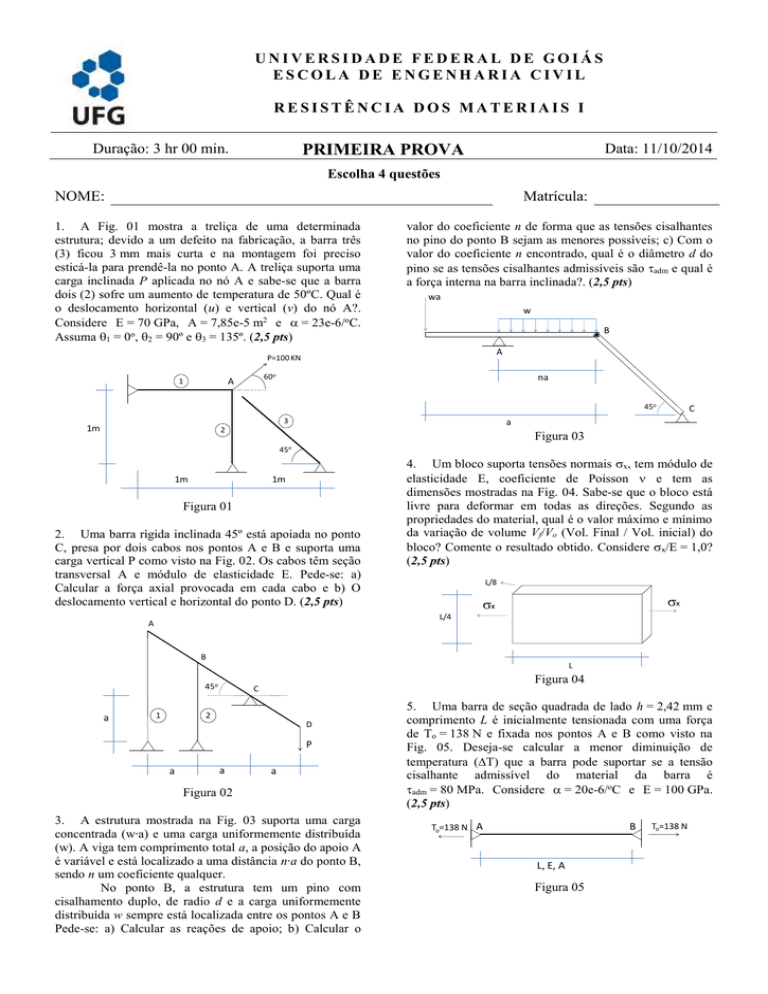
1. A Fig. 01 mostra a treliça de uma determinada
estrutura; devido a um defeito na fabricação, a barra três
(3) ficou 3 mm mais curta e na montagem foi preciso
esticá-la para prendê-la no ponto A. A treliça suporta uma
carga inclinada P aplicada no nó A e sabe-se que a barra
dois (2) sofre um aumento de temperatura de 50ºC. Qual é
o deslocamento horizontal (u) e vertical (v) do nó A?.
Considere E = 70 GPa, A = 7,85e-5 m2 e  = 23e-6/oC.
Assuma 1 = 0o, 2 = 90º e 3 = 135º. (2,5 pts)
valor do coeficiente n de forma que as tensões cisalhantes
no pino do ponto B sejam as menores possíveis; c) Com o
valor do coeficiente n encontrado, qual é o diâmetro d do
pino se as tensões cisalhantes admissíveis são adm e qual é
a força interna na barra inclinada?. (2,5 pts)
wa
w
B
A
P=100 KN
60o
A
1
na
45o
3
1m
C
a
2
Figura 03
45o
1m
1m
Figura 01
2. Uma barra rígida inclinada 45º está apoiada no ponto
C, presa por dois cabos nos pontos A e B e suporta uma
carga vertical P como visto na Fig. 02. Os cabos têm seção
transversal A e módulo de elasticidade E. Pede-se: a)
Calcular a força axial provocada em cada cabo e b) O
deslocamento vertical e horizontal do ponto D. (2,5 pts)
4. Um bloco suporta tensões normais x, tem módulo de
elasticidade E, coeficiente de Poisson  e tem as
dimensões mostradas na Fig. 04. Sabe-se que o bloco está
livre para deformar em todas as direções. Segundo as
propriedades do material, qual é o valor máximo e mínimo
da variação de volume Vf/Vo (Vol. Final / Vol. inicial) do
bloco? Comente o resultado obtido. Considere x/E = 1,0?
(2,5 pts)
L/8
x
x
L/4
A
B
L
45o
a
1
Figura 04
C
2
D
P
a
a
a
Figura 02
3. A estrutura mostrada na Fig. 03 suporta uma carga
concentrada (w∙a) e uma carga uniformemente distribuída
(w). A viga tem comprimento total a, a posição do apoio A
é variável e está localizado a uma distância n∙a do ponto B,
sendo n um coeficiente qualquer.
No ponto B, a estrutura tem um pino com
cisalhamento duplo, de radio d e a carga uniformemente
distribuída w sempre está localizada entre os pontos A e B
Pede-se: a) Calcular as reações de apoio; b) Calcular o
5. Uma barra de seção quadrada de lado h = 2,42 mm e
comprimento L é inicialmente tensionada com uma força
de To = 138 N e fixada nos pontos A e B como visto na
Fig. 05. Deseja-se calcular a menor diminuição de
temperatura (T) que a barra pode suportar se a tensão
cisalhante admissível do material da barra é
adm = 80 MPa. Considere  = 20e-6/oC e E = 100 GPa.
(2,5 pts)
To=138 N A
B
L, E, A
Figura 05
To=138 N
EQUAÇÕES NECESSÁRIAS NA SOLUÇÃO
Equilíbrio:
 Fx  0,  Fy  0,  M  0
Tensão normal:   P A
Tensão cisalhante:   V A
Fator de segurança: F.S.  Pult Padm
Deformação normal:   L f  Lo Lo


Coeficiente de Poisson:     t  l
Binômio de Newton: 1  a  n  1  n a
Pequena deformações: 1   n  1  n
Lei de Hooke:   E ;   G 
Lei de Hooke Generalizada
1
 x   x   y   z   T
E
1
 y   y   x   z    T
E
1
 z   z   x   y   T
E






 xy 
 xy
G


;  xz 
 xz
;  yz 
G
E
Relação entre G e E: G 
2 1   
L
Deformação axial:  
 yz
G
 A( x) E dx
P( x)
0
L

Deformação por temperatura:  T   T dx
0
Rigidez de mola: K x  P
Variação de comprimento de uma barra:
e  eu cos    ev sen     T L  s