Exame 1

TEM – Transferência de Energia e Massa 2015/16,
Exame 1 (18 de Junho)
Problema 1.1 (3/20)
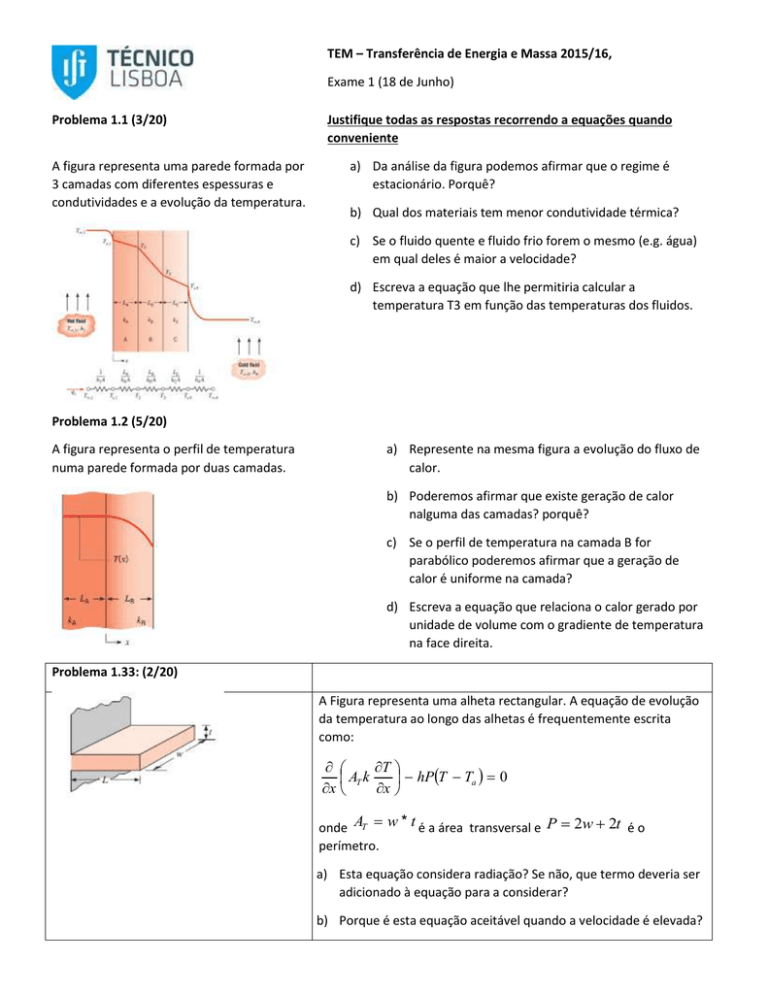
A figura representa uma parede formada por
3 camadas com diferentes espessuras e
condutividades e a evolução da temperatura.
Justifique todas as respostas recorrendo a equações quando
conveniente
a) Da análise da figura podemos afirmar que o regime é
estacionário. Porquê?
b) Qual dos materiais tem menor condutividade térmica?
c) Se o fluido quente e fluido frio forem o mesmo (e.g. água)
em qual deles é maior a velocidade?
d) Escreva a equação que lhe permitiria calcular a
temperatura T3 em função das temperaturas dos fluidos.
Problema 1.2 (5/20)
A figura representa o perfil de temperatura
numa parede formada por duas camadas.
a) Represente na mesma figura a evolução do fluxo de
calor.
b) Poderemos afirmar que existe geração de calor
nalguma das camadas? porquê?
c) Se o perfil de temperatura na camada B for
parabólico poderemos afirmar que a geração de
calor é uniforme na camada?
d) Escreva a equação que relaciona o calor gerado por
unidade de volume com o gradiente de temperatura
na face direita.
Problema 1.33: (2/20)
A Figura representa uma alheta rectangular. A equação de evolução
da temperatura ao longo das alhetas é frequentemente escrita
como:
 
T 
 AT k
  hPT  Ta   0
x 
x 
onde AT  w * t é a área transversal e P  2w  2t é o
perímetro.
a) Esta equação considera radiação? Se não, que termo deveria ser
adicionado à equação para a considerar?
b) Porque é esta equação aceitável quando a velocidade é elevada?
TEM – Transferência de Energia e Massa 2015/16
Exame 1 – Parte 2, 18 de Junho
Grupo 2.1: Acerca das equações de evolução
(2.5 valores/20)
A equação de evolução para Oxigénio Dissolvido numa geometria 1D genérica é:
O2
O
  k O2 
u 2 
 kO Csat  O2   kd CBOD
t
x
x  c p x 
onde C sat é a concentração de saturação e C BOD é a concentração de Carência Biológica de Oxigénio, i.e. o
oxigénio necessário à respiração da matéria orgânica transportada pela água.
a) Estará a produção de O2 pela fotossíntese incluída nesta equação?
b) A concentração de O2 depende da temperatura da água. Através de que termo da equação?
c) Em corpos de água naturais com biomassas elevadas o perigo de ocorrência de eventos de baixa
concentração de oxigénio é maior em noites calmas (sem vento). Que termos da equação quantificam
esses efeitos (biomassa elevada e vento reduzido)?
Grupo 2.2: Resolução Numérica das equações
(2.5 valores/20)
a) As Séries de Taylor são usadas para calcular derivadas, transformando a equações diferenciais em
equações algébricas e fornecendo informações sobre erros de truncatura. Os métodos semi-implícitos
têm precisão de segunda ordem. O que é que isso significa?
b) São os métodos upwind sempre melhores do que as diferenças centrais?
c) As diferenças centrais podem gerar concentrações negativas. Porquê?
(2.5 valores/20)
Grupo 2.3: Condições de Fronteira
1. As trocas de calor sensível e de calor latente através da superfície livre de um rio são descritas por
equações com formas semelhantes. Contudo o calor sensível pode contribuir para aumentar a
temperatura da água, mas o calor latente não pode. Porquê?
2. As descargas antropogénicas podem ser do tipo pontual ou difuso. Os caudais e as concentrações das
descargas pontuais são normalmente de fácil caracterização. Escreva a equação que calcula a
modificação da concentração na célula de descarga.
(2.5 valores/20)
Grupo 2.4: Resultados de um modelo 1D
O modelo 1D de advecção difusão só pode representar sistemas lineares, não sendo adequado para simular
lagos convencionais, mas pode ser usado para simular um lago comprido e estreito (e.g. um canal sem
escoamento). Neste caso a velocidade seria nula e não haveria advecção.
1. Como seria a distribuição final de concentração num lago devida a uma descarga instantânea sem
decaimento? e com decaimento?
2. Como evoluiria a concentração nesse lago se ocorresse uma descarga contínua sem decaimento? Com
decaimento, seria possível atingir uma solução estacionária?