S: Uma roda de 10 kg e I = 0,156 kg·m gira sem deslizar e, ao

EXEMPLO 1
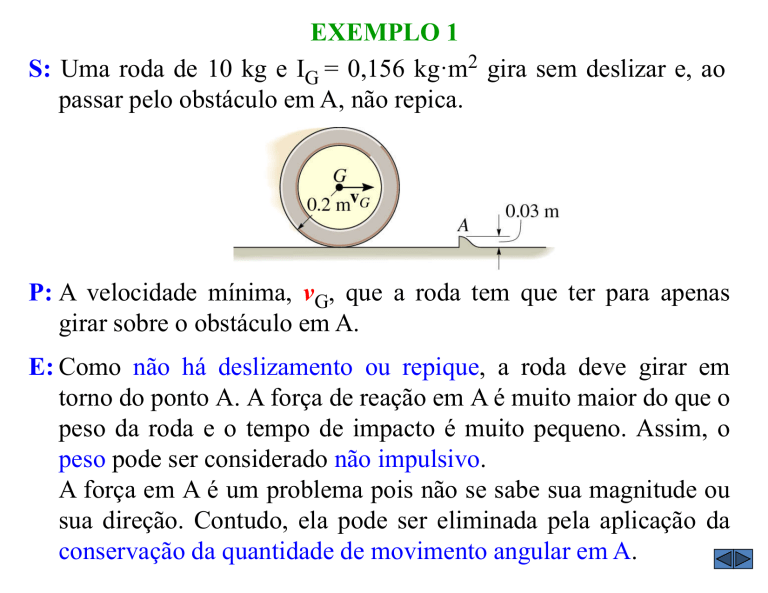
S: Uma roda de 10 kg e IG = 0,156 kg·m2 gira sem deslizar e, ao
passar pelo obstáculo em A, não repica.
P: A velocidade mínima, vG, que a roda tem que ter para apenas
girar sobre o obstáculo em A.
E: Como não há deslizamento ou repique, a roda deve girar em
torno do ponto A. A força de reação em A é muito maior do que o
peso da roda e o tempo de impacto é muito pequeno. Assim, o
peso pode ser considerado não impulsivo.
A força em A é um problema pois não se sabe sua magnitude ou
sua direção. Contudo, ela pode ser eliminada pela aplicação da
conservação da quantidade de movimento angular em A.
EXEMPLO 1 (cont.)
Solução:
Diagrama de impulso e quantidade de movimento:
Conservação de quantidade de movimento angular:
(HA)1 = (HA)2
r' m (vG)1 + IG 1 = r m (vG)2 + IG 2
(0,2 – 0,03) 10 (vG)1 + 0,156 1 = 0,2(10) (vG)2 + 0,156 2
Cinemática: Como não há deslizamento,  = vG/r = 5 vG. Levando
esse resultado na equação de conservação, tem-se
(vG)2 = 0,892 (vG)1
EXEMPLO 1 (cont.)
Para completar a solução, o princípio da conservação de energia
pode ser usado. Como ele não pode ser usado no impacto (por
quê?), ele será aplicado logo após o impacto.
Para rolar pelo obstáculo, a roda tem que ir para a posição 3 a
partir da 2. Quando (vG)2 é mínima, (vG)3 é zero (por quê?).
Equação de conservação de energia: T2 + V2 = T3 + V3
{0,5 (10) (vG)22 + 0,5 (0,156) 22 } + 0 = 0 + 98,1 (0,03)
Como 2 = 5 (vG)2 e (vG)2 = 0,892 (vG)1 , tem-se que
(vG)1 = 0,729 m/s
EXEMPLO 2
S: Duas crianças (mA = mB = 30 kg) sentam-se na borda de um
carrossel, de massa igual a 180 kg e raio de giração kz = 0,6 m.
P: A velocidade angular do
carrossel se a criança A
pula fora horizontalmente
na direção tangencial +,
com a velocidade de 2 m/s,
em relação ao carrossel.
E: Desenhar um diagrama de impulso e quantidade de movimento
e usar a conservação de quantidade de movimento angular para
encontrar a velocidade angular.
EXEMPLO 2 (cont.)
Solução:
Diagrama de impulso e
quantidade de movimento:
Equação de conservação de quantidade
de movimento angular:
∑(H)1 = ∑(H)2
mB
M
mA
2 rad/s
= 180 (0,6)2  + (30)  (0,75) 2
vA/M = 2 m/s
=
mB
M

180 (0,6)2 (2) + 2 × {(30) 2 (0,75) 2}
mA
+ (30) (0,75  + 2) (0,75)
 197,1 = 98,55  + 45
Resolvendo a equação acima, obtém-se
 = 1,54 rad/s .