(Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos

LISTA – UERJ – 3ª SÉRIE
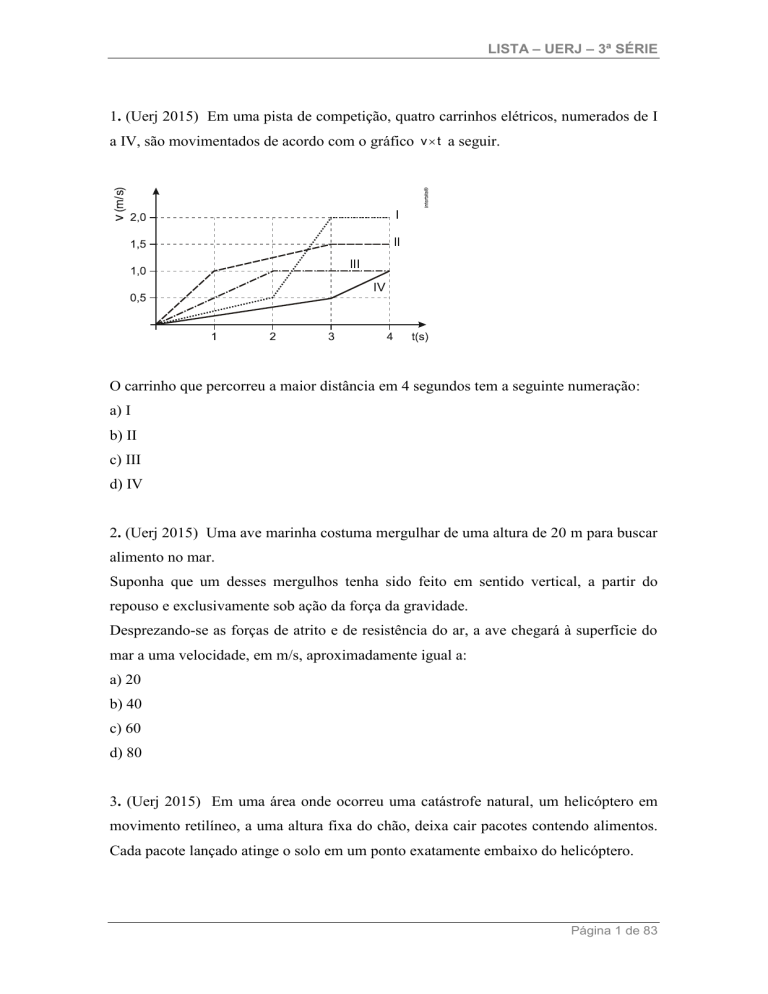
1. (Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos, numerados de I
a IV, são movimentados de acordo com o gráfico v  t a seguir.
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
2. (Uerj 2015) Uma ave marinha costuma mergulhar de uma altura de 20 m para buscar
alimento no mar.
Suponha que um desses mergulhos tenha sido feito em sentido vertical, a partir do
repouso e exclusivamente sob ação da força da gravidade.
Desprezando-se as forças de atrito e de resistência do ar, a ave chegará à superfície do
mar a uma velocidade, em m/s, aproximadamente igual a:
a) 20
b) 40
c) 60
d) 80
3. (Uerj 2015) Em uma área onde ocorreu uma catástrofe natural, um helicóptero em
movimento retilíneo, a uma altura fixa do chão, deixa cair pacotes contendo alimentos.
Cada pacote lançado atinge o solo em um ponto exatamente embaixo do helicóptero.
Página 1 de 83
LISTA – UERJ – 3ª SÉRIE
Desprezando forças de atrito e de resistência, pode-se afirmar que as grandezas
velocidade e aceleração dessa aeronave são classificadas, respectivamente, como:
a) variável − nula
b) nula − constante
c) constante − nula
d) variável − variável
4. (Uerj 2015) Um esquiador, com 70kg de massa, colide elasticamente contra uma
árvore a uma velocidade de 72km / h.
Calcule, em unidades do SI, o momento linear e a energia cinética do esquiador no
instante da colisão.
5. (Uerj 2015) Um carro, em um trecho retilíneo da estrada na qual trafegava, colidiu
frontalmente com um poste. O motorista informou um determinado valor para a
velocidade de seu veículo no momento do acidente. O perito de uma seguradora apurou,
no entanto, que a velocidade correspondia a exatamente o dobro do valor informado
pelo motorista.
Considere Ec1 a energia cinética do veículo calculada com a velocidade informada pelo
motorista e Ec 2 aquela calculada com o valor apurado pelo perito.
A razão
a)
1
2
b)
1
4
Ec1
corresponde a:
Ec 2
c) 1
d) 2
6. (Uerj 2015) Observe o aumento da profundidade de prospecção de petróleo em águas
brasileiras com o passar dos anos, registrado na figura a seguir.
Página 2 de 83
LISTA – UERJ – 3ª SÉRIE
Considerando os dados acima, calcule, em atm, a diferença entre a pressão
correspondente à profundidade de prospecção de petróleo alcançada no ano de 1977 e
aquela alcançada em 2003.
7. (Uerj 2015) Considere um corpo sólido de volume V. Ao flutuar em água, o volume
de sua parte submersa é igual a
V
; quando colocado em óleo, esse volume passa a valer
8
V
.
6
Com base nessas informações, conclui-se que a razão entre a densidade do óleo e a da
água corresponde a:
a) 0,15
b) 0,35
c) 0,55
d) 0,75
8. (Uerj 2015) Uma empresa japonesa anunciou que pretende construir o elevador mais
rápido do mundo. Ele alcançaria a velocidade de 72 km / h, demorando apenas 43
segundos para chegar do térreo ao 95º andar de um determinado prédio.
Considere os seguintes dados:
Página 3 de 83
LISTA – UERJ – 3ª SÉRIE
- aceleração constante do elevador;
- altura de cada andar do prédio igual a 4 m;
- massa do elevador, mais sua carga máxima, igual a 3000 kg.
Estime a força média que atua sobre o elevador, quando está com carga máxima, no
percurso entre o térreo e o 95º andar.
9. (Uerj 2015) Admita uma colisão frontal totalmente inelástica entre um objeto que se
move com velocidade inicial v0 e outro objeto inicialmente em repouso, ambos com
mesma massa.
Nessa situação, a velocidade com a qual os dois objetos se movem após a colisão
equivale a:
a)
v0
2
b)
v0
4
c) 2v0
d) 4v 0
10. (Uerj 2015) No mapa abaixo, está representada a variação média da temperatura
dos oceanos em um determinado mês do ano. Ao lado, encontra-se a escala, em graus
Celsius, utilizada para a elaboração do mapa.
Página 4 de 83
LISTA – UERJ – 3ª SÉRIE
Determine, em graus kelvins, o módulo da variação entre a maior e a menor temperatura
da escala apresentada.
11. (Uerj 2015)
Um mergulhador precisa encher seu tanque de mergulho, cuja
capacidade é de 1,42  102 m3, a uma pressão de 140 atm e sob temperatura constante.
O volume de ar, em m3, necessário para essa operação, à pressão atmosférica de 1 atm, é
aproximadamente igual a:
a)
1
4
b)
1
2
c) 2
d) 4
12. (Uerj 2015) Um corpo de massa igual a 500g, aquecido por uma fonte térmica cuja
potência é constante e igual a 100cal / min, absorve integralmente toda a energia
fornecida por essa fonte. Observe no gráfico a variação de temperatura do corpo em
função do tempo.
Página 5 de 83
LISTA – UERJ – 3ª SÉRIE
Calcule o calor específico da substância da qual o corpo é composto, bem como a
capacidade térmica desse corpo.
13. (Uerj 2015) Para aquecer 1L de água contida em um recipiente de capacidade
térmica desprezível, uma pessoa dispõe de um aquecedor elétrico portátil cuja potência
é de 1273 W, quando submetido a uma tensão de 127V. Considere que toda a energia
fornecida pelo aquecedor seja absorvida pela água.
Nessas condições, calcule a variação de temperatura da água após o aquecedor inserido
no recipiente ficar ligado por 165 segundos.
14. (Uerj 2015) Um lápis com altura de 20cm é colocado na posição vertical a 50cm
do vértice de um espelho côncavo. A imagem conjugada pelo espelho é real e mede
5cm.
Calcule a distância, em centímetros, da imagem ao espelho.
15. (Uerj 2015) O princípio físico do funcionamento de alternadores e transformadores,
comprovável de modo experimental, refere-se à produção de corrente elétrica por meio
da variação de um campo magnético aplicado a um circuito elétrico.
Esse princípio se fundamenta na denominada Lei de:
a) Newton
b) Ampère
c) Faraday
d) Coulomb
Página 6 de 83
LISTA – UERJ – 3ª SÉRIE
16. (Uerj 2015) Partículas de carga elétrica q e massa m penetram no plano horizontal
de uma região do espaço na qual existe um campo magnético de intensidade B, normal
a esse plano. Ao entrar na região, as partículas são submetidas a um selecionador de
velocidades que deixa passar apenas aquelas com velocidade v0 .
Admita que, na região do campo magnético, a trajetória descrita por uma das partículas
selecionadas seja circular.
Escreva a expressão matemática para o raio dessa trajetória em função de:
- massa, carga e velocidade da partícula;
- intensidade do campo magnético.
17. (Uerj 2015) Para localizar obstáculos totalmente submersos, determinados navios
estão equipados com sonares, cujas ondas se propagam na água do mar. Ao atingirem
um obstáculo, essas ondas retornam ao sonar, possibilitando assim a realização de
cálculos que permitem a localização, por exemplo, de um submarino.
Admita uma operação dessa natureza sob as seguintes condições:
- temperatura constante da água do mar;
- velocidade da onda sonora na água igual a 1450 m/s;
- distância do sonar ao obstáculo igual a 290 m.
Página 7 de 83
LISTA – UERJ – 3ª SÉRIE
Determine o tempo, em segundos, decorrido entre o instante da emissão da onda pelo
sonar e o de seu retorno após colidir com o submarino.
18. (Uerj 2014) O cérebro humano demora cerca de 0,36 segundos para responder a um
estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo esse
tempo de resposta para acionar o freio.
Determine a distância que um carro a 100 km/h percorre durante o tempo de resposta do
motorista e calcule a aceleração média imposta ao carro se ele para totalmente em 5
segundos.
19. (Uerj 2014) Em um longo trecho retilíneo de uma estrada, um automóvel se desloca
a 80 km/h e um caminhão a 60 km/h, ambos no mesmo sentido e em movimento
uniforme. Em determinado instante, o automóvel encontra-se 60 km atrás do caminhão.
O intervalo de tempo, em horas, necessário para que o automóvel alcance o caminhão é
cerca de:
a) 1
b) 2
c) 3
d) 4
20. (Uerj 2014) O gráfico abaixo representa a variação da velocidade dos carros A e B
que se deslocam em uma estrada.
Página 8 de 83
LISTA – UERJ – 3ª SÉRIE
Determine as distâncias percorridas pelos carros A e B durante os primeiros cinco
segundos do percurso. Calcule, também, a aceleração do carro A nos dois primeiros
segundos.
21. (Uerj 2014) O corpo de um aspirador de pó tem massa igual a 2,0 kg. Ao utilizá-lo,
durante um dado intervalo de tempo, uma pessoa faz um esforço sobre o tubo 1 que
resulta em uma força de intensidade constante igual a 4,0 N aplicada ao corpo do
aspirador. A direção dessa força é paralela ao tubo 2, cuja inclinação em relação ao solo
é igual a 60º, e puxa o corpo do aspirador para perto da pessoa.
Considere sen 60° = 0,87, cos 60° = 0,5 e também que o corpo do aspirador se move
sem atrito. Durante esse intervalo de tempo, a aceleração do corpo do aspirador, em
m/s2, equivale a:
a) 0,5
b) 1,0
c) 1,5
d) 2,0
22. (Uerj 2014) A imagem abaixo ilustra uma bola de ferro após ser disparada por um
canhão antigo.
Página 9 de 83
LISTA – UERJ – 3ª SÉRIE
Desprezando-se a resistência do ar, o esquema que melhor representa as forças que
atuam sobre a bola de ferro é:
a)
b)
c)
d)
23. (Uerj 2014) Um chuveiro elétrico com resistência igual a 5Ω é conectado a uma
rede elétrica que fornece 120 V de tensão eficaz.
Determine a energia elétrica, em kWh, consumida pelo chuveiro durante 10 minutos.
24. (Uerj 2014) Duas gotas de orvalho caem de uma mesma folha de árvore, estando
ambas a uma altura h do solo. As gotas possuem massas m1 e m2 , sendo m2  2m1. Ao
atingirem o solo, suas velocidades e energias cinéticas são, respectivamente, v1, E1 e
v 2 , E2.
Desprezando o atrito e o empuxo, determine as razões
v1
E
e 1.
v2
E2
25. (Uerj 2014) Um automóvel de massa igual a 942 kg é suspenso por um elevador
hidráulico cujo cilindro de ascensão tem diâmetro de 20 cm.
Calcule a pressão a ser aplicada ao cilindro para manter o automóvel em equilíbrio a
uma determinada altura.
26. (Uerj 2014) A figura abaixo ilustra uma ferramenta utilizada para apertar ou
desapertar determinadas peças metálicas.
Página 10 de 83
LISTA – UERJ – 3ª SÉRIE
Para apertar uma peça, aplicando-se a menor intensidade de força possível, essa
ferramenta deve ser segurada de acordo com o esquema indicado em:
a)
b)
c)
d)
27. (Uerj 2014) A intensidade F da força de atração gravitacional entre o Sol e um
planeta é expressa pela seguinte relação:
Página 11 de 83
LISTA – UERJ – 3ª SÉRIE
FG
mM
r2
G − constante universal da gravitação
m − massa do planeta
M − massa do Sol
r − raio da órbita do planeta
Admitindo que o movimento orbital dos planetas do sistema solar é circular uniforme,
estime a massa do Sol.
28. (Uerj 2014) Observe na tabela os valores das temperaturas dos pontos críticos de
fusão e de ebulição, respectivamente, do gelo e da água, à pressão de 1 atm, nas escalas
Celsius e Kelvin.
Pontos críticos
Temperatura
°C
K
Fusão
0
273
Ebulição
100
373
Considere que, no intervalo de temperatura entre os pontos críticos do gelo e da água, o
mercúrio em um termômetro apresenta uma dilatação linear.
Nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é
igual a
a) 20
b) 30
c) 40
d) 60
29. (Uerj 2014) Um sistema é constituído por uma pequena esfera metálica e pela água
contida em um reservatório. Na tabela, estão apresentados dados das partes do sistema,
antes de a esfera ser inteiramente submersa na água.
Página 12 de 83
LISTA – UERJ – 3ª SÉRIE
Partes do sistema
esfera
metálica
água do
reservatório
Temperatura
inicial (°C)
Capacidade
térmica
(cal/°C)
50
2
30
2000
A temperatura final da esfera, em graus Celsius, após o equilíbrio térmico com a água
do reservatório, é cerca de:
a) 20
b) 30
c) 40
d) 50
30. (Uerj 2014) A energia consumida por uma pessoa adulta em um dia é igual a 2 400
kcal.
Determine a massa de gelo a 0°C que pode ser totalmente liquefeita pela quantidade de
energia consumida em um dia por um adulto. Em seguida, calcule a energia necessária
para elevar a temperatura dessa massa de água até 30°C.
31. (Uerj 2014) Um lápis é colocado perpendicularmente à reta que contém o foco e o
vértice de um espelho esférico côncavo.
Considere os seguintes dados:
- comprimento do lápis = 10 cm;
- distância entre o foco e o vértice = 40 cm;
- distância entre o lápis e o vértice = 120 cm.
Calcule o tamanho da imagem do lápis.
Página 13 de 83
LISTA – UERJ – 3ª SÉRIE
32. (Uerj 2014) No experimento de Millikan, que determinou a carga do elétron,
pequenas gotas de óleo eletricamente carregadas são borrifadas entre duas placas
metálicas paralelas. Ao aplicar um campo elétrico uniforme entre as placas, da ordem de
2  104 V / m, é possível manter as gotas em equilíbrio, evitando que caiam sob a ação da
gravidade.
Considerando que as placas estão separadas por uma distância igual a 2 cm, determine a
diferença de potencial necessária para estabelecer esse campo elétrico entre elas.
33. (Uerj 2014) Cinco resistores de mesma resistência R estão conectados à bateria
ideal E de um automóvel, conforme mostra o esquema:
Inicialmente, a bateria fornece ao circuito uma potência P I. Ao estabelecer um curtocircuito entre os pontos M e N, a potência fornecida é igual a PF.
A razão
a)
7
9
b)
14
15
PF
é dada por:
PI
c) 1
d)
7
6
34. (Uerj 2014)
No circuito, uma bateria B está conectada a três resistores de
resistências R1, R2 e R3:
Página 14 de 83
LISTA – UERJ – 3ª SÉRIE
Sabe-se que R2 = R3 = 2R1.
A relação entre as potências P1, P2 e P3, respectivamente associadas a R1, R2 e R3, pode
ser expressa como:
a) P1 = P2 = P3
b) 2P1 = P2 = P3
c) 4P1 = P2 = P3
d) P1 = 2P2 = 2P3
35. (Uerj 2014)
Considere uma onda sonora que se propaga na atmosfera com
frequência igual a 10 Hz e velocidade igual a 340 m/s.
Determine a menor distância entre dois pontos da atmosfera nos quais, ao longo da
direção de propagação, a amplitude da onda seja máxima.
36. (Uerj 2013) Um motorista dirige um automóvel em um trecho plano de um viaduto.
O movimento é retilíneo e uniforme.
A intervalos regulares de 9 segundos, o motorista percebe a passagem do automóvel
sobre cada uma das juntas de dilatação do viaduto.
Sabendo que a velocidade do carro é 80 km/h, determine a distância entre duas juntas
consecutivas.
37. (Uerj 2013) Três pequenas esferas, E1, E2 e E3 , são lançadas em um mesmo
instante, de uma mesma altura, verticalmente para o solo. Observe as informações da
tabela:
Página 15 de 83
LISTA – UERJ – 3ª SÉRIE
Esfera Material
Velocidade inicial
E1
chumbo
v1
E2
alumínio
v2
E3
vidro
v3
A esfera de alumínio é a primeira a alcançar o solo; a de chumbo e a de vidro chegam
ao solo simultaneamente.
A relação entre v1, v 2 e v3 está indicada em:
a) v1  v3  v 2
b) v1  v3  v2
c) v1  v3  v2
d) v1  v3  v2
38. (Uerj 2013)
Três blocos de mesmo volume, mas de materiais e de massas
diferentes, são lançados obliquamente para o alto, de um mesmo ponto do solo, na
mesma direção e sentido e com a mesma velocidade.
Observe as informações da tabela:
Material
bloco
do
Alcance do lançamento
chumbo
A1
ferro
A2
granito
A3
A relação entre os alcances A1, A2 e A3 está apresentada em:
a) A1 > A2 > A3
b) A1 < A2 < A3
c) A1 = A2 > A3
d) A1 = A2 = A3
39. (Uerj 2013) Um bloco de madeira encontra-se em equilíbrio sobre um plano
inclinado de 45º em relação ao solo. A intensidade da força que o bloco exerce
Página 16 de 83
LISTA – UERJ – 3ª SÉRIE
perpendicularmente ao plano inclinado é igual a 2,0 N. Entre o bloco e o plano
inclinado, a intensidade da força de atrito, em newtons, é igual a:
a) 0,7
b) 1,0
c) 1,4
d) 2,0
40. (Uerj 2013) Uma pessoa adulta, para realizar suas atividades rotineiras, consome
em média, 2500 kcal de energia por dia.
Calcule a potência média, em watts, consumida em um dia por essa pessoa para realizar
suas atividades.
Utilize: 1 cal = 4,2 J.
41. (Uerj 2013) Uma pequena caixa é lançada em direção ao solo, sobre um plano
inclinado, com velocidade igual a 3,0 m/s. A altura do ponto de lançamento da caixa,
em relação ao solo, é igual a 0,8 m.
Considerando que a caixa desliza sem atrito, estime a sua velocidade ao atingir o solo.
Utilize: Aceleração da gravidade = 10 m/s2.
42. (Uerj 2013) Observe, na figura a seguir, a representação de uma prensa hidráulica,
na qual as forças F1 e F2 atuam, respectivamente, sobre os êmbolos dos cilindros I e II.
Admita que os cilindros estejam totalmente preenchidos por um líquido.
O volume do cilindro II é igual a quatro vezes o volume do cilindro I, cuja altura é o
triplo da altura do cilindro II.
Página 17 de 83
LISTA – UERJ – 3ª SÉRIE
A razão
F2
entre as intensidades das forças, quando o sistema está em equilíbrio,
F1
corresponde a:
a) 12
b) 6
c) 3
d) 2
43. (Uerj 2013) Um homem de massa igual a 80 kg está em repouso e em equilíbrio
sobre uma prancha rígida de 2,0 m de comprimento, cuja massa é muito menor que a do
homem.
A prancha está posicionada horizontalmente sobre dois apoios, A e B, em suas
extremidades, e o homem está a 0,2 m da extremidade apoiada em A.
A intensidade da força, em newtons, que a prancha exerce sobre o apoio A equivale a:
a) 200
b) 360
c) 400
d) 720
44. (Uerj 2013) Sabe-se que a pressão que um gás exerce sobre um recipiente é
decorrente dos choques de suas moléculas contra as paredes do recipiente.
Diminuindo em 50% o volume do recipiente que contém um gás ideal, sem alterar sua
temperatura, estabeleça a razão entre a pressão final e a pressão inicial.
45. (Uerj 2013) Em um laboratório, as amostras X e Y, compostas do mesmo material,
foram aquecidas a partir da mesma temperatura inicial até determinada temperatura
final.
Durante o processo de aquecimento, a amostra X absorveu uma quantidade de calor
maior que a amostra Y.
Considerando essas amostras, as relações entre os calores específicos cX e cY, as
capacidades térmicas CX e CY e as massas mX e mY são descritas por:
a) cX = cY CX > CY mX > mY
b) cX > cY CX = CY mX = mY
c) cX = cY CX > CY mX = mY
Página 18 de 83
LISTA – UERJ – 3ª SÉRIE
d) cX > cY CX = CY mX > mY
46. (Uerj 2013) Uma pessoa, com temperatura corporal igual a 36,7°C, bebe
1
litro de
2
água a 15°C.
Admitindo que a temperatura do corpo não se altere até que o sistema atinja o equilíbrio
térmico, determine a quantidade de calor, em calorias, que a água ingerida absorve do
corpo dessa pessoa.
Utilize: Calor específico da água = 1,0 cal g C; Massa específica da água = 1 g/cm3.
47. (Uerj 2013) Considere duas amostras, X e Y, de materiais distintos, sendo a massa
de X igual a quatro vezes a massa de Y.
As amostras foram colocadas em um calorímetro e, após o sistema atingir o equilíbrio
térmico, determinou-se que a capacidade térmica de X corresponde ao dobro da
capacidade térmica de Y.
Admita que c X e c Y sejam os calores específicos, respectivamente, de X e Y.
A razão
a)
1
4
b)
1
2
cX
é dada por:
cY
c) 1
d) 2
48. (Uerj 2013) Um raio luminoso monocromático, inicialmente deslocando-se no
vácuo, incide de modo perpendicular à superfície de um meio transparente, ou seja, com
ângulo de incidência igual a 0°. Após incidir sobre essa superfície, sua velocidade é
reduzida a
5
do valor no vácuo.
6
Utilizando a relação
sen θ1 θ1

para ângulos menores que 10°, estime o ângulo de
sen θ2 θ2
refringência quando o raio atinge o meio transparente com um ângulo de incidência
igual a 3°.
Página 19 de 83
LISTA – UERJ – 3ª SÉRIE
49. (Uerj 2013) Um jovem com visão perfeita observa um inseto pousado sobre uma
parede na altura de seus olhos. A distância entre os olhos e o inseto é de 3 metros.
Considere que o inseto tenha 3 mm de tamanho e que a distância entre a córnea e a
retina, onde se forma a imagem, é igual a 20 mm.
Determine o tamanho da imagem do inseto.
50. (Uerj 2013) Em uma experiência, três lâmpadas idênticas {L1, L2, L3} foram
inicialmente associadas em série e conectadas a uma bateria E de resistência interna
nula. Cada uma dessas lâmpadas pode ser individualmente ligada à bateria E sem se
queimar.
Observe o esquema desse circuito, quando as três lâmpadas encontram-se acesas:
Em seguida, os extremos não comuns de L1 e L2 foram conectados por um fio metálico,
conforme ilustrado abaixo:
A afirmativa que descreve o estado de funcionamento das lâmpadas nessa nova
condição é:
a) As três lâmpadas se apagam.
b) As três lâmpadas permanecem acesas.
c) L1 e L2 se apagam e L3 permanece acesa.
d) L3 se apaga e L1 e L2 permanecem acesas.
Página 20 de 83
LISTA – UERJ – 3ª SÉRIE
51. (Uerj 2013) Ao ser conectado a uma rede elétrica que fornece uma tensão eficaz de
200 V, a taxa de consumo de energia de um resistor ôhmico é igual a 60 W.
Determine o consumo de energia, em kWh, desse resistor, durante quatro horas, ao ser
conectado a uma rede que fornece uma tensão eficaz de 100 V.
52. (Uerj 2013) Duas lâmpadas, L1 e L2 , estão conectadas em paralelo a uma bateria de
automóvel. A corrente em L1 é igual a
1
da corrente em L2 .
3
Admita que P1 e P2 sejam as potências dissipadas, respectivamente, por L1 e L2 .
A razão
a)
1
9
b)
1
3
P1
corresponde a:
P2
c) 1
d) 3
53. (Uerj 2013) Um transformador que fornece energia elétrica a um computador está
conectado a uma rede elétrica de tensão eficaz igual a 120 V.
A tensão eficaz no enrolamento secundário é igual a 10 V, e a corrente eficaz no
computador é igual a 1,2 A.
Estime o valor eficaz da corrente no enrolamento primário do transformador.
54. (Uerj 2013) Vulcões submarinos são fontes de ondas acústicas que se propagam no
mar com frequências baixas, da ordem de 7,0 Hz, e comprimentos de onda da ordem de
220 m.
Utilizando esses valores, calcule a velocidade de propagação dessas ondas.
55. (Uerj 2013) A partícula káon, eletricamente neutra, é constituída por duas partículas
eletricamente carregadas: um quark d e um antiquark s.
A carga do quark d é igual a 
1
do módulo da carga do elétron, e a carga do quark s
3
tem mesmo módulo e sinal contrário ao da carga de um antiquark s.
Página 21 de 83
LISTA – UERJ – 3ª SÉRIE
Ao quark s é atribuída uma propriedade denominada estranheza, a qual pode ser
calculada pela seguinte fórmula:
S  2Q 
1
3
S – estranheza
Q – razão entre a carga do quark s e o módulo da carga do elétron
Assim, o valor da estranheza de um quark s é igual a:
a)
1
3
b) 1
c) 
1
3
d) –1
56. (Uerj 2012) Dois carros, A e B, em movimento retilíneo acelerado, cruzam um
mesmo ponto em t = 0 s. Nesse instante, a velocidade v 0 de A é igual à metade da de B,
e sua aceleração a corresponde ao dobro da de B.
Determine o instante em que os dois carros se reencontrarão, em função de v 0 e a.
57. (Uerj 2012) Galileu Galilei, estudando a queda dos corpos no vácuo a partir do
repouso, observou que as distâncias percorridas a cada segundo de queda correspondem
a uma sequência múltipla dos primeiros números ímpares, como mostra o gráfico
abaixo.
Página 22 de 83
LISTA – UERJ – 3ª SÉRIE
Determine a distância total percorrida após 4 segundos de queda de um dado corpo. Em
seguida, calcule a velocidade desse corpo em t = 4 s.
58. (Uerj 2012) Uma pequena pedra amarrada a uma das extremidades de um fio
inextensível de 1 m de comprimento, preso a um galho de árvore pela outra
extremidade, oscila sob ação do vento entre dois pontos equidistantes e próximos à
vertical. Durante 10 s, observou-se que a pedra foi de um extremo ao outro, retornando
ao ponto de partida, 20 vezes.
Calcule a frequência de oscilação desse pêndulo.
59. (Uerj 2012) Uma pessoa empurrou um carro por uma distância de 26 m, aplicando
uma força F de mesma direção e sentido do deslocamento desse carro. O gráfico abaixo
representa a variação da intensidade de F, em newtons, em função do deslocamento d,
em metros.
Desprezando o atrito, o trabalho total, em joules, realizado por F, equivale a:
a) 117
b) 130
c) 143
d) 156
60. (Uerj 2012)
Em uma partida de tênis, após um saque, a bola, de massa
aproximadamente igual a 0,06 kg, pode atingir o solo com uma velocidade de 60 m/s.
Admitindo que a bola esteja em repouso no momento em que a raquete colide contra
ela, determine, no SI, as variações de sua quantidade de movimento e de sua energia
cinética.
Página 23 de 83
LISTA – UERJ – 3ª SÉRIE
61. (Uerj 2012) Considere uma balança de dois pratos, na qual são pesados dois
recipientes idênticos, A e B.
Os dois recipientes contêm água até a borda. Em B, no entanto, há um pedaço de
madeira flutuando na água.
Nessa situação, indique se a balança permanece ou não em equilíbrio, justificando sua
resposta.
62. (Uerj 2012) Um cilindro sólido e homogêneo encontra-se, inicialmente, apoiado
sobre sua base no interior de um recipiente. Após a entrada de água nesse recipiente até
um nível máximo de altura H, que faz o cilindro ficar totalmente submerso, verifica-se
que a base do cilindro está presa a um fio inextensível de comprimento L. Esse fio está
fixado no fundo do recipiente e totalmente esticado.
Observe a figura:
Em função da altura do nível da água, o gráfico que melhor representa a intensidade da
força F que o fio exerce sobre o cilindro é:
Página 24 de 83
LISTA – UERJ – 3ª SÉRIE
a)
b)
c)
d)
63. (Uerj 2012) Observe a tabela abaixo, que apresenta as massas de alguns corpos em
movimento uniforme.
Corpos
leopardo
Massa Velocidade
(kg)
(km/h)
120
60
automóvel 1100
70
caminhão
20
3600
Admita que um cofre de massa igual a 300 kg cai, a partir do repouso e em queda livre
de uma altura de 5 m. Considere Q1 , Q2 , Q3 e Q4 , respectivamente, as quantidades de
movimento do leopardo, do automóvel, do caminhão e do cofre ao atingir o solo. As
magnitudes dessas grandezas obedecem relação indicada em:
Página 25 de 83
LISTA – UERJ – 3ª SÉRIE
a) Q1  Q4  Q2  Q3
b) Q4  Q1  Q2  Q3
c) Q1  Q4  Q3  Q2
d) Q4  Q1  Q3  Q2
64. (Uerj 2012) Uma balança romana consiste em uma haste horizontal sustentada por
um gancho em um ponto de articulação fixo. A partir desse ponto, um pequeno corpo P
pode ser deslocado na direção de uma das extremidades, a fim de equilibrar um corpo
colocado em um prato pendurado na extremidade oposta. Observe a ilustração:
Quando P equilibra um corpo de massa igual a 5 kg, a distância d de P até o ponto de
articulação é igual a 15 cm.
Para equilibrar um outro corpo de massa igual a 8 kg, a distância, em centímetros, de P
até o ponto de articulação deve ser igual a:
a) 28
b) 25
c) 24
d) 20
65. (Uerj 2012) Na tirinha a seguir, o diálogo entre a maçã, a bola e a Lua, que estão
sob a ação da Terra, faz alusão a uma lei da Física.
Página 26 de 83
LISTA – UERJ – 3ª SÉRIE
Aponte a constante física introduzida por essa lei.
Indique a razão entre os valores dessa constante física para a interação gravitacional
Lua-Terra e para a interação maçã-Terra.
66. (Uerj 2012) Em um reator nuclear, a energia liberada na fissão de 1 g de urânio é
utilizada para evaporar a quantidade de 3,6  104 kg de água a 227ºC e sob 30 atm,
necessária para movimentar uma turbina geradora de energia elétrica. Admita que o
vapor d’água apresenta comportamento de gás ideal. O volume de vapor d’água, em
litros, gerado a partir da fissão de 1 g de urânio, corresponde a:
a) 1,32  105
b) 2,67  106
c) 3,24  107
d) 7,42  108
67. (Uerj 2012) Considere X e Y dois corpos homogêneos, constituídos por substâncias
distintas, cujas massas correspondem, respectivamente, a 20 g e 10 g.
O gráfico abaixo mostra as variações da temperatura desses corpos em função do calor
absorvido por eles durante um processo de aquecimento.
Página 27 de 83
LISTA – UERJ – 3ª SÉRIE
Determine as capacidades térmicas de X e Y e, também, os calores específicos das
substâncias que os constituem.
68. (Uerj 2012) Um copo contendo 200 g de água é colocado no interior de um forno
de micro-ondas.
Quando o aparelho é ligado, a energia é absorvida pela água a uma taxa de 120 cal/s.
Sabendo que o calor específico da água é igual a 1 cal.g-1.°C-1, calcule a variação de
temperatura da água após 1 minuto de funcionamento do forno.
69. (Uerj 2012) Três pequenas esferas metálicas, E1, E2 e E3, eletricamente carregadas e
isoladas, estão alinhadas, em posições fixas, sendo E2 equidistante de E1 e E3. Seus raios
possuem o mesmo valor, que é muito menor que as distâncias entre elas, como mostra a
figura:

E1

E2

E3
As cargas elétricas das esferas têm, respectivamente, os seguintes valores:
• Q1  20 μC
• Q2   4 μC
• Q3  1 μC
Admita que, em um determinado instante, E1 e E2 são conectadas por um fio metálico;
após alguns segundos, a conexão é desfeita.
Página 28 de 83
LISTA – UERJ – 3ª SÉRIE
Nessa nova configuração, determine as cargas elétricas de E1 e E2 e apresente um
esquema com a direção e o sentido da força resultante sobre E3.
70. (Uerj 2012) Em uma experiência, foram conectados em série uma bateria de 9 V e
dois resistores, de resistências R1  1600  e R2  800 . Em seguida, um terceiro
resistor, de resistência R3, foi conectado em paralelo a R2. Com o acréscimo de R3, a
diferença de potencial no resistor R2 caiu para
1
do valor inicial.
3
Considerando a nova configuração, calcule o valor da resistência equivalente total do
circuito.
71. (Uerj 2012) Um chuveiro elétrico, alimentado por uma tensão eficaz de 120 V,
pode funcionar em dois modos: verão e inverno. Considere os seguintes dados da
tabela:
Modos
Verão
Potência Resistência
(W)
()
1000
RV
Inverno 2000
A relação
RI
RI
corresponde a:
RV
a) 0,5
b) 1,0
c) 1,5
d) 2,0
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Uma sala é iluminada por um circuito de lâmpadas incandescentes em paralelo.
Considere os dados abaixo:
− a corrente elétrica eficaz limite do fusível que protege esse circuito é igual a 10 A;
− a tensão eficaz disponível é de 120 V;
− sob essa tensão, cada lâmpada consome uma potência de 60 W.
Página 29 de 83
LISTA – UERJ – 3ª SÉRIE
72. (Uerj 2012) O número máximo de lâmpadas que podem ser mantidas acesas
corresponde a:
a) 10
b) 15
c) 20
d) 30
73. (Uerj 2012) A resistência equivalente, em ohms, de apenas 8 lâmpadas acesas é
cerca de:
a) 30
b) 60
c) 120
d) 240
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Três bolas − X, Y e Z − são lançadas da borda de uma mesa, com velocidades iniciais
paralelas ao solo e mesma direção e sentido. A tabela abaixo mostra as magnitudes das
massas e das velocidades iniciais das bolas.
Bolas
Massa Velocidade inicial
(g)
(m/s)
X
5
20
Y
5
10
Z
10
8
74. (Uerj 2012) As relações entre os respectivos alcances horizontais A x , A y e A z das
bolas X, Y e Z, com relação à borda da mesa, estão apresentadas em:
a) A x < A y < A z
b) A y = A x = A z
Página 30 de 83
LISTA – UERJ – 3ª SÉRIE
c) A z < A y < A x
d) A y < A z < A x
75. (Uerj 2012) As relações entre os respectivos tempos de queda t x , t y e t z das bolas
X, Y e Z estão apresentadas em:
a) t x < t y < t z
b) t y < t z < t x
c) t z < t y < t x
d) t y = t x = t z
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Considere as leis de Newton e as informações a seguir.
Uma pessoa empurra uma caixa sobre o piso de uma sala. As forças aplicadas sobre a
caixa na direção do movimento são:
− Fp : força paralela ao solo exercida pela pessoa;
− Fa : força de atrito exercida pelo piso.
A caixa se desloca na mesma direção e sentido de Fp .
A força que a caixa exerce sobre a pessoa é FC .
76. (Uerj 2012) Se o deslocamento da caixa ocorre com velocidade constante, as
magnitudes das forças citadas apresentam a seguinte relação:
a) Fp  FC  Fa
b) Fp  FC  Fa
c) Fp  FC  Fa
d) Fp  FC  Fa
Página 31 de 83
LISTA – UERJ – 3ª SÉRIE
77. (Uerj 2012) Se o deslocamento da caixa ocorre com aceleração constante, na
mesma direção e sentido de Fp , as magnitudes das forças citadas apresentam a seguinte
relação:
a) Fp  Fc  Fa
b) Fp  Fc  Fa
c) Fp  Fc  Fa
d) Fp  Fc  Fa
78. (Uerj 2011) Uma partícula se afasta de um ponto de referência O, a partir de uma
posição inicial A, no instante t = 0 s, deslocando-se em movimento retilíneo e uniforme,
sempre no mesmo sentido.
A distância da partícula em relação ao ponto O, no instante t = 3,0 s, é igual a 28,0 m e,
no instante t = 8,0 s, é igual a 58,0 m.
Determine a distância, em metros, da posição inicial A em relação ao ponto de
referência O.
79. (Uerj 2011) No interior de um avião que se desloca horizontalmente em relação ao
solo, com velocidade constante de 1000 km/h, um passageiro deixa cair um copo.
Observe a ilustração abaixo, na qual estão indicados quatro pontos no piso do corredor
do avião e a posição desse passageiro.
O copo, ao cair, atinge o piso do avião próximo ao ponto indicado pela seguinte letra:
a) P
b) Q
c) R
d) S
Página 32 de 83
LISTA – UERJ – 3ª SÉRIE
80. (Uerj 2011) Um corpo de massa igual a 6,0 kg move-se com velocidade constante
de 0,4 m/s, no intervalo de 0 s a 0,5 s.
Considere que, a partir de 0,5 s, esse corpo é impulsionado por uma força de módulo
constante e de mesmo sentido que a velocidade, durante 1,0 s.
O gráfico abaixo ilustra o comportamento da força em função do tempo.
Calcule a velocidade do corpo no instante t = 1,5 s.
81. (Uerj 2011) Um patinador cujo peso total é 800 N, incluindo os patins, está parado
em uma pista de patinação em gelo. Ao receber um empurrão, ele começa a se deslocar.
A força de atrito entre as lâminas dos patins e a pista, durante o deslocamento, é
constante e tem módulo igual a 40 N.
Estime a aceleração do patinador imediatamente após o início do deslocamento.
82. (Uerj 2011) Um homem arrasta uma cadeira sobre um piso plano, percorrendo em
linha reta uma distância de 1 m. Durante todo o percurso, a força que ele exerce sobre a
cadeira possui intensidade igual a 4 N e direção de 60° em relação ao piso.
O gráfico que melhor representa o trabalho T, realizado por essa força ao longo de todo
o deslocamento d, está indicado em:
a)
Página 33 de 83
LISTA – UERJ – 3ª SÉRIE
b)
c)
d)
83. (Uerj 2011) As unidades joule, kelvin, pascal e newton pertencem ao SI - Sistema
Internacional de Unidades.
Dentre elas, aquela que expressa a magnitude do calor transferido de um corpo a outro é
denominada:
a) joule
b) kelvin
c) pascal
d) newton
84. (Uerj 2011) Um bloco maciço está inteiramente submerso em um tanque cheio de
água, deslocando-se verticalmente para o fundo em movimento uniformente acelerado.
A razão entre o peso do bloco e o empuxo sobre ele é igual a 12,5.
A aceleração do bloco, em m/s2, é aproximadamente de:
a) 2,5
b) 9,2
c) 10,0
d) 12,0
Página 34 de 83
LISTA – UERJ – 3ª SÉRIE
85. (Uerj 2011) Uma prancha homogênea de comprimento igual a 5,0 m e massa igual
a 10,0 kg encontra-se apoiada nos pontos A e B, distantes 2,0 m entre si e equidistantes
do ponto médio da prancha.
Sobre a prancha estão duas pessoas, cada uma delas com massa igual a 50 kg.
Observe a ilustração:
Admita que uma dessas pessoas permaneça sobre o ponto médio da prancha.
Nessas condições, calcule a distância máxima, em metros, que pode separar as duas
pessoas sobre a prancha, mantendo o equilíbrio.
86. (Uerj 2011) A bola utilizada em uma partida de futebol é uma esfera de diâmetro
interno igual a 20 cm. Quando cheia, a bola apresenta, em seu interior, ar sob pressão de
1,0 atm e temperatura de 27 ºC.
Considere  = 3, R = 0,080 atm.L.mol-1.k-1 e, para o ar, comportamento de gás ideal e
massa molar igual a 30 g.mol-1.
No interior da bola cheia, a massa de ar, em gramas, corresponde a:
a) 2,5
b) 5,0
c) 7,5
d) 10,0
87. (Uerj 2011) Um professor realizou com seus alunos o seguinte experimento para
observar fenômenos térmicos:
- colocou, inicialmente, uma quantidade de gás ideal em um recipiente adiabático;
- comprimiu isotermicamente o gás à temperatura de 27 ºC, até a pressão de 2,0 atm;
- liberou, em seguida, a metade do gás do recipiente;
- verificou, mantendo o volume constante, a nova temperatura de equilíbrio, igual a 7
ºC.
Página 35 de 83
LISTA – UERJ – 3ª SÉRIE
Calcule a pressão do gás no recipiente ao final do experimento.
88. (Uerj 2011) Um raio de luz vindo do ar, denominado meio A, incide no ponto O da
superfície de separação entre esse meio e o meio B, com um ângulo de incidência igual
a 7º.
No interior do meio B, o raio incide em um espelho côncavo E, passando pelo foco
principal F.
O centro de curvatura C do espelho, cuja distância focal é igual a 1,0 m, encontra-se a
1,0 m da superfície de separação dos meios A e B.
Observe o esquema:
Considere os seguintes índices de refração:
- nA = 1,0 (meio A)
- nB = 1,2 (meio B)
Determine a que distância do ponto O o raio emerge, após a reflexão no espelho.
89. (Uerj 2011) Em um laboratório, um pesquisador colocou uma esfera eletricamente
carregada em uma câmara na qual foi feito vácuo.
O potencial e o módulo do campo elétrico medidos a certa distância dessa esfera valem,
respectivamente, 600 V e 200 V/m.
Determine o valor da carga elétrica da esfera.
90. (Uerj 2011) Observe a representação do trecho de um circuito elétrico entre os
pontos X e Y, contendo três resistores cujas resistências medem, em ohms, a, b e c.
Página 36 de 83
LISTA – UERJ – 3ª SÉRIE
Admita que a sequência (a, b, c) é uma progressão geométrica de razão
1
e que a
2
resistência equivalente entre X e Y mede 2,0 Ω . O valor, em ohms, de (a + b + c) é igual
a:
a) 21,0
b) 22,5
c) 24,0
d) 24,5
91. (Uerj 2011) No circuito abaixo, o voltímetro V e o amperímetro A indicam,
respectivamente, 18 V e 4,5 A.
Considerando como ideais os elementos do circuito, determine a força eletromotriz E da
bateria.
92. (Uerj 2011) Para dar a partida em um caminhão, é necessário que sua bateria de 12
V estabeleça uma corrente de 100 A durante um minuto.
A energia, em joules, fornecida pela bateria, corresponde a:
a) 2,0 x 101
b) 1,2 x 102
Página 37 de 83
LISTA – UERJ – 3ª SÉRIE
c) 3,6 x 103
d) 7,2 x 104
93. (Uerj 2011) A sirene de uma fábrica produz sons com frequência igual a 2640 Hz.
Determine o comprimento de onda do som produzido pela sirene em um dia cuja
velocidade de propagação das ondas sonoras no ar seja igual a 1188 km/h.
94. (Uerj 2011) Considere as seguintes informações do Modelo Padrão da Física de
Partículas:
- prótons e nêutrons são constituídos por três quarks dos tipos u e d;
- o quark u tem carga elétrica positiva igual a
2
do módulo da carga do elétron;
3
- um próton p é constituído por dois quarks u e um quark d, ou seja, p = uud.
Determine o número de quarks u e o número de quarks d que constituem um nêutron n.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Um trem em alta velocidade desloca-se ao longo de um trecho retilíneo a uma
velocidade constante de 108 km/h. Um passageiro em repouso arremessa
horizontalmente ao piso do vagão, de uma altura de 1 m, na mesma direção e sentido do
deslocamento do trem, uma bola de borracha que atinge esse piso a uma distância de 5
m do ponto de arremesso.
95. (Uerj 2011) O intervalo de tempo, em segundos, que a bola leva para atingir o piso
é cerca de:
a) 0,05
b) 0,20
c) 0,45
d) 1,00
96. (Uerj 2011) Se a bola fosse arremessada na mesma direção, mas em sentido oposto
ao do deslocamento do trem, a distância, em metros, entre o ponto em que a bola atinge
o piso e o ponto de arremesso seria igual a:
Página 38 de 83
LISTA – UERJ – 3ª SÉRIE
a) 0
b) 5
c) 10
d) 15
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
A figura abaixo representa o plano inclinado ABFE, inserido em um paralelepípedo
retângulo ABCDEFGH de base horizontal, com 6 m de altura CF , 8 m de comprimento
BC e 15 m de largura AB , em repouso, apoiado no solo.
97. (Uerj 2011) Considere o deslocamento em movimento retilíneo de um corpo P1 de
M até N e de um corpo P2 de A até F.
Admita as seguintes informações:
- P1 e P2 são corpos idênticos;
- F1 e F2 são, respectivamente, as componentes dos pesos de P1 e P2 ao longo das
respectivas trajetórias;
- M e N são, respectivamente, os pontos médios das arestas AB e EF.
Admita um outro corpo de massa igual a 20 kg que desliza com atrito, em movimento
retilíneo, do ponto F ao ponto B, com velocidade constante.
A força de atrito, em newtons, entre a superfície deste corpo e o plano inclinado é cerca
de:
a) 50
b) 100
Página 39 de 83
LISTA – UERJ – 3ª SÉRIE
c) 120
d) 200
98. (Uerj 2011) Considere o deslocamento em movimento retilíneo de um corpo P1 de
M até N e de um corpo P2 de A até F.
Admita as seguintes informações:
- P1 e P2 são corpos idênticos;
- F1 e F2 são, respectivamente, as componentes dos pesos de P1 e P2 ao longo das
respectivas trajetórias;
- M e N são, respectivamente, os pontos médios das arestas AB e EF.
Considerando esses dados, a razão
a)
17
6
b)
4
3
c)
15
3
d)
13
3
F1
equivale a:
F2
99. (Uerj 2010) Um foguete persegue um avião, ambos com velocidades constantes e
mesma direção. Enquanto o foguete percorre 4,0 km, o avião percorre apenas 1,0 km.
Admita que, em um instante t1, a distância entre eles é de 4,0 km e que, no instante t2, o
foguete alcança o avião.
No intervalo de tempo t2 – t1, a distância percorrida pelo foguete, em quilômetros,
corresponde aproximadamente a:
a) 4,7
b) 5,3
c) 6,2
d) 8,6
100. (Uerj 2010) A figura a seguir representa uma piscina completamente cheia de
água, cuja forma é um prisma hexagonal regular.
Página 40 de 83
LISTA – UERJ – 3ª SÉRIE
Admita que:
– A, B, C e D representam vértices desse prisma;
– o volume da piscina é igual a 450 m3 e
3
AB
=
;
CD 10
– um atleta nada, em linha reta, do ponto A até o ponto médio da aresta CD , utilizando
apenas glicose como fonte de energia para seus músculos.
A velocidade média do atleta no percurso definido foi igual a 1,0 m/s.
O intervalo de tempo, em segundos, gasto nesse percurso equivale a cerca de:
a) 12,2
b) 14,4
c) 16,2
d) 18,1
Página 41 de 83
LISTA – UERJ – 3ª SÉRIE
Gabarito:
Resposta
da
questão
1:
[B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o
eixo dos tempos. Calculando cada uma delas:

 2  0,51  1 2  0,5  1,25  2  3,75 m.
2  0,5

DI 
2
2





1,5  1 2  1,5  1  0,5  2,5  1,5  4,5 m.
1 1

DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
 IV
2
2
Resposta
da
questão
2:
[A]
Usando a equação de Torricelli com a = g = 10 m/s2 e ΔS  h  20m.
v 2  v02  2g h  v 2  0  2  10  20  400 
v  20 m/s.
Resposta
da
questão
3:
[C]
Depois de lançado, a componente horizontal da velocidade vetorial do pacote não mais
se altera, pois não há forças aplicadas no pacote nessa direção. Ou seja, nessa direção o
movimento é retilíneo e uniforme. Se cada pacote lançado atinge o solo em um ponto
Página 42 de 83
LISTA – UERJ – 3ª SÉRIE
exatamente embaixo do helicóptero, então a aeronave também está em MRU, sendo,
então, constante a velocidade e nula e aceleração.
Resposta
da
questão
4:
questão
5:
questão
6:
Dados: m  70 kg; v  72 km/h  20 m/s.

p  m v  70  20  p  1.400 kg  m/s.


2
m v 2 70  20 

E


 EC  14.000 J.
 C
2
2
Resposta
da
[B]

m v2
Ec 1 

2

2

m 2 v 
Ec

 2
2

 Ec 2  4
mv
Resposta
2

Ec 1 1
 .
Ec 2 4
2
da
A diferença de profundidade entre os pontos citados é:
Δh  1.886 124  1.762 m.
Considerando que a cada 10 m a pressão hidrostática aumenta de, aproximadamente,
1atm, a diferença de pressão é:
Δp 
1.762

10
Resposta
Δp  176 atm.
da
questão
7:
[D]
Se o corpo está parcialmente imerso, o empuxo e o peso estão equilibrados. Sendo m e
V a massa e o volume do corpo, respectivamente, Vi o volume imerso, dC a densidade
do corpo e dL a densidade do líquido, temos:
Página 43 de 83
LISTA – UERJ – 3ª SÉRIE
P  E  dC V g  dL Vi g
dC Vi
 .
dL V

Aplicando os dados da questão nessa expressão:
V
 d
dC
1
 C  8 

 dágua
V
dágua 8
dC Vi 


dL V 
V
 dC
dC
1
 6 


V
dóleo 6
 dóleo
 
dC
d
1 6 6 3
 óleo    

dágua
dC
8 1 8 4
dóleo
 0,75.
dágua
Resposta
da
questão
8:
A questão está muito mal formulada, pois ela não especifica:
- se o elevador para ao atingir o 95º andar (caso esse não seja o último andar), ou se
passa por ele com velocidade de 72 km / h;
- se essa força média é a resultante, ou a tração no cabo que puxa o elevador.
Vamos considerar três situações, aplicando o teorema do impulso em cada uma delas.
1ª) O elevador para no 95º andar e a força média pedida é a resultante (R).
IR  ΔQ  R Δt  m Δv  R  43  3.000 0  0  
R  0 N.
2ª) O elevador passa pelo 95º andar com velocidade de 72 km/h (20 m/s) e a força
média pedida é a resultante (R).
IR  ΔQ  R Δt  m Δv  R  43  3.000  20  0 
R  1.395 N.
3ª) O elevador passa pelo 95º andar com velocidade de 72 km/h (20 m/s) e a força
média pedida é a força de tração no cabo (F).
IR  ΔQ  F  P Δt  m Δv  F  30.000  43  3.000  20  0  
F
60.000
 30.000 
43
Resposta
F  31.400 N.
da
questão
9:
[A]
Página 44 de 83
LISTA – UERJ – 3ª SÉRIE
Pela conservação da quantidade de movimento:
m v0  2 m v

v
v 0
2
Resposta
da
questão
10:
As variações de temperatura nas escalas Celsius (θ) e Kelvin (T) são numericamente
iguais.
Δθ  4,5   3,5   8 °C 
Resposta
ΔT  8 K.
da
questão
11:
[C]
Considerando o processo isotérmico e comportamento de gás perfeito para o ar, da
equação geral dos gases:
p V p0 V0

 140  1,42  102  1 V2  V2  198  102 m3 
T
T0
V2  2 m3 .
Resposta
da
questão
12:
Dados: m  500 g; P  100 cal/min.
Q  m c ΔT


Q
P  Δt  Q  PΔt

 m c ΔT  P Δt  c 
100  30 
PΔt


m ΔT 500  50  10 
c  0,15 cal/g  °C.
C  m c  500  0,15  
Resposta
C  75 cal/°C.
da
questão
13:
Dados: P  1.273 W; V  1 L  m  1.000 g; Δt  165 s; c  4,2 J/g  °C.
Página 45 de 83
LISTA – UERJ – 3ª SÉRIE
Q  m c ΔT


Q
P  Δt  Q  PΔt

 m c ΔT  PΔt  ΔT 
PΔt 1.273  165


m c 1.000  4,2
ΔT  50 °C.
Resposta
da
questão
14:
Dados: h  20 cm; p  50 cm; h'  5 cm.
Supondo que o referido espelho côncavo seja esférico, temos:
p'  h'
p'   5 




p
h
50
20
Resposta
p'  12,5 cm.
da
questão
15:
[C]
A lei de Neumann Faraday afirma que a força eletromotriz induzida (ε ) numa bobina é
à variação do fluxo magnético (ΔΦ) relativamente ao tempo (Δt).
Resposta
da
questão
16:
Se o movimento é circular uniforme, a força magnética atua como resultante centrípeta.
Fmag  Rcent  q v B 
Resposta
Δt 

R
mv
.
qB
da
2 d 2  290


v
1.450
Resposta
m v2
R
questão
17:
questão
18:
Δt  0,4 s.
da
 Distância percorrida durante o tempo de resposta:
Dados: v = 100 km/h = (100/3,6) m/s; Δt  0,36s.
D  v Δt 
100
 0,36  D  10 m.
3,6
 Aceleração média de frenagem:
Página 46 de 83
LISTA – UERJ – 3ª SÉRIE
Dados: v0 = 100 km/h = (100/3,6) m/s; v = 0; Δt  5s.
Supondo trajetória retilínea, a aceleração escalar é:
100
Δv 0 
3,6
a

 a  5,6 m/s2.
Δt
5
Resposta
da
questão
19:
[C]
Como se deslocam no mesmo sentido, a velocidade relativa entre eles é:
vrel  v A  vC  80  60  20 km / h.
Sendo a distância relativa, Srel  60km, o tempo necessário para o alcance é:
t 
Srel 60

 t  3 h.
vrel
20
Resposta
da
questão
20:
 Distâncias percorridas pelos carros:
No gráfico v  t a distância percorrida é numericamente igual à área entre a linha do
gráfico e o eixo dos tempos. Assim:
53

DA  2  2  DA  8 m.


DA   4  1  2    3  1  DB  8 m.
 2




 Aceleração do carro A:
Dados: v0 = 0; v = 2 m/s; Δt  2s.
Entendendo por aceleração apenas a aceleração escalar do veículo, temos:
a
Δv 2  0

 a  1 m/s2.
Δt
2
Resposta
da
questão
21:
[B]
Página 47 de 83
LISTA – UERJ – 3ª SÉRIE
A resultante das forças sobre o corpo do aspirador é a componente horizontal da força
Fx  aplicada no cabo.
Aplicando o Princípio Fundamental da Dinâmica:
 1
Fx  m a  Fcos60  m a  4    2 a 
2
a  1 m / s2 .
Resposta
da
questão
22:
[A]
Após o lançamento, a única força que age sobre a bola é seu próprio peso, vertical e
para baixo.
Resposta
da
questão
23:
Dados: R  5Ω; U  120 V; Δ t  10min  1/ 6h.
ΔE  P Δt 
U2
1202 1
Δt 
  480 W  h  ΔE  0,48 kW  h.
R
5
6
Resposta
da
questão
24:
 Razão entre as velocidades:
Pela conservação da energia mecânica, podemos mostrar que a velocidade independe da
massa:
final
inicial
EMec
 EMec

m v2
mgh  v
2
v
2 g h  v1  v 2  1  1.
v2
Página 48 de 83
LISTA – UERJ – 3ª SÉRIE
 Razão entre as energias cinéticas:
Dado: m2 = 2 m1.
m1 v12
E1
m1
E1 1
2



 .
2
E 2 m 2 v2
2 m1
E2 2
2
Resposta
da
questão
25:
Dados: m = 942 kg; D  20cm  2  101m; g = 10 m/s2.
Se há equilíbrio, a intensidade da força normal aplicada ao cilindro tem a mesma
intensidade do peso. Assim:
p
mg
P
4  942  10


A π D2
3,14  4  102
4
Resposta
 p  3  105 N/m2.
da
questão
26:
[D]
Quanto maior o braço da alavanca (distância da linha de ação da força ao apoio), menor
a intensidade da força para se obter o mesmo torque.
Resposta
da
questão
27:
Dados: r  1,5 1011m; G  6,7 1011N  m2  kg2; π  3,14; T  1 ano  3 107 s.
Sendo circular a órbita do planeta, a força gravitacional exerce a função de resultante
centrípeta.
2
 2π  3
 T  r
GM m

 m ω2 r  M  
2
G
r
F  Rcent 
M

4  9,9   1,5  1011

4 π2 r 3
G T2

3
6,7  10   3  10 
11
 M
7
2

1,3  1035
6  104

M  2,2  1030 kg.
Página 49 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
28:
questão
29:
[C]
Da relação entre essas duas escalas:
TC  TK  273  313  273  TC  40 C.
Resposta
da
[B]
A análise dos dados dispensa cálculos. A capacidade térmica da esfera metálica é
desprezível em relação à da água contida no reservatório, portanto, a temperatura da
água praticamente não se altera, permanecendo em cerca de 30 °C.
Mas, comprovemos com os cálculos.
Considerando o sistema água-esfera termicamente isolado:
Qesf  Qágua  0  Cesf Tesf  Cágua Tágua  0 
2  T  50   2.000  T  30   0  2 T  100  2.000 T  60.000  0
2.002 T  60.100  0  T 

60.100
 30,0998 C 
2.002
T  30 C.
Resposta
da
questão
30:
questão
31:
 Massa de gelo fundida:
Dados: Q = 2.400 kcal; Lf = 80 kcal/kg.
Da expressão do calor latente:
Q  m Lf
 m
Q 2 400

Lf
80
 m  30 kg.
 Energia para elevar até 30 °C:
Dados: m = 30 kg; c = 1 kcal/kg°C; Δθ  30C.
Da expressão do calor sensível:
Q  m c Δθ  Q  30  1 30  Q  900 kcal.
Resposta
da
Dados: f = 40 cm; p = 120 cm; h = 10 cm.
Página 50 de 83
LISTA – UERJ – 3ª SÉRIE
Aplicando as equações dos espelhos esféricos:
1 1 1
 
p' f p
h' p'

h
p
 p' 

p f
120  40

pf
80
h'
60

10 120
Resposta
 p'  60 cm.
 h'  5 cm.
da
questão
32:
questão
33:
Dados: E  2 104 V / m; d  2cm  2 102m.
U  E d  2  104  2  102  4  102  U  400 V.
Resposta
da
[D]
Estabelecendo um curto-circuito, popularmente conhecido como “chupeta”, entre os
pontos M e N, os três resistores em paralelo não mais funcionam.
Para as duas situações inicial e final, as respectivas resistências equivalentes são:
R
7

RI  3  2 R  3 R.


R  2 R.
 F

Calculando as potências dissipadas:
Página 51 de 83
LISTA – UERJ – 3ª SÉRIE

3 E2
E2
PI 

7R
7 R

U2

3
Pd 

R

E2
PF 
2 R


 
Resposta
da
PF
7 R
E2


PI 2 R 3 E 2

PF 7
 .
PI 6
questão
34:
[D]
Como R1 = R2, e sendo a ligação em paralelo, os dois resistores são percorridos pela
mesma corrente (i). Portanto, a corrente em R1 é o dobro da corrente em R2 e R3 (I = 2
i). Assim:
P2  P3  2 R1 i2


2
P1  R1  2 i   P1  4 R1 i2
Resposta
 P1  2 P2  2 P3 .
da
questão
35:
A menor distância (d) entre dois pontos de amplitude máxima é o próprio comprimento
de onda ( λ ). Da equação fundamental da ondulatória:
dλ 
v 340

f
10
 d  34 m.
Resposta
v
Δs 
da
questão
36:
da
questão
37:
Δs
80
Δs

(m / s) 
Δt
3,6
9(s)
9.80
 m
3,6
 Δs  200m
Resposta
[B]
Supondo a ausência do atrito com o ar, podemos concluir que o movimento das esferas
é uniformemente variado e, como tal,
Página 52 de 83
LISTA – UERJ – 3ª SÉRIE
h  v0 .t 
g.t2
g.t2
h g.t
 v0 .t  h 
 v0  
2
2
t 2
Onde v0 corresponde à velocidade inicial de lançamento:
Como os tempos de queda das esferas são iguais, temos que suas velocidades de
lançamento são iguais; portanto, as velocidades v1 e v3 são iguais.
Como a esfera de alumínio foi a primeira a chegar ao solo, concluímos que sua
velocidade inicial é a maior de todas. Assim temos, v1  v3  v2 .
Resposta
da
questão
38:
[D]
Para um objeto lançado obliquamente com velocidade inicial v0 , formando um ângulo
θ com a horizontal, num local onde o campo gravitacional tem intensidade g, o alcance
horizontal A é dado pela expressão:
v 2
A  0 sen  2θ
g
Essa expressão nos mostra que o alcance horizontal independe da massa. Portanto, os
três blocos apresentarão o mesmo alcance:
A1 = A2 = A3.
Resposta
da
questão
39:
[D]
Dado: N  2 N; θ  45.
A figura ilustra a situação.
Página 53 de 83
LISTA – UERJ – 3ª SÉRIE
O bloco está sujeito a duas forças: O peso P e a força aplicada pelo plano F . Como
ele está em equilíbrio, a resultante dessas forças é nula, ou seja, elas têm mesma
intensidade e sentidos opostos.
Assim, da figura:
F
F
tg 45  at  1  at  Fat  2 N.
N
2
Resposta
P
da
questão
40:
da
questão
41:
Q 2500000.4,2  J

Δt
86400  s
 P  121,5w
Resposta
Eco  EPo  Ecf  EPf
mv02
mv02
mv2f
mv2f
 mgh0 
 mghf 
 mgh0 
 mghf
2
2
2
2
No solo h f é nulo logo:
32
 10.0,8 
2
v2f
2
Vf2  25
 Vf  5m / s
Página 54 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
42:
[A]
Pelo teorema de Pascal aplicado em prensas hidráulicas, temos:
F1 F2

A1 A2
O volume dos cilindros é dado por: V  A.h.
Nas condições apresentadas no enunciado, temos:
V2  4.V1
A2 .h2  4.A1.h1
A 2 .h  4.A1.3h
A 2  12.A1
Assim:
F1
F
F
 2  2  12
A1 12A1
F1
Resposta
da
questão
43:
[D]
Página 55 de 83
LISTA – UERJ – 3ª SÉRIE
| NA | .2,0 | P | .1,8
| NA | .2,0  80.10.1,8
| NA | .2,0  80.18
| NA | 80.9
 | NA | 720N
Resposta
da
questão
44:
questão
45:
Condições iniciais do gás: v0  v p0  p θ0  θ
Condições finais do gás: v f  0,5v pf  ? θf  θ
p0  v0 pf  v f
p
p  v pf  0,5 v



 f  2
θo
θf
θ
θ
p0
Resposta
da
[A]
Como as duas amostras são do mesmo material, elas apresentam o mesmo calor
específico:
c X  c Y  c.
Sendo QX e QY as quantidades de calor absorvidas pelas amostras X e Y,
respectivamente:

QX  CX Δθ


QY  CY Δθ

CX  mX c


CY  mY c
QX  QY  CX  CY .
CX  CY  mX  mY .
Resposta
da
questão
46:
A partir dos dados apresentados no enunciado, temos:
d 1
g
3
cm
1
g 1000 g

ml
l
Página 56 de 83
LISTA – UERJ – 3ª SÉRIE
Assim sendo, concluímos que meio litro de água corresponderá a 500 gramas.
Calculemos agora a variação da temperatura sofrida pela água ingerida:
Δθ  36,7  15  21,7
Utilizando a equação fundamental da calorimetria:
Q  m  c  Δθ
Substituindo pelos valores encontrados, temos:
Q  500.1 21,7
 Q  10850 cal
Resposta
da
questão
47:
[B]
Dados apresentados no enunciado:
mx  4my
Cx  2Cy
A relação entre a capacidade térmica de um corpo e sua massa é dada por:
C  m c , em que “c” corresponde ao calor específico sensível. Assim sendo, temos:
mx  c x  2  my  c y  4my  c x  2  my  c y
2  cx  cy

cx 1

cy 2
Página 57 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
48:
A partir da Lei de Snell, temos:
n1  senθ1  n2  senθ2
c
c
 senθ1 
 senθ2
v1
v2
v 2  senθ1  v1  senθ2
Em que “c” representa a velocidade da luz no vácuo.
Como a velocidade da luz em um determinado meio independe do ângulo de incidência,
temos:
5
v1  c e v2  c
6
Substituindo na expressão acima:
5
c  senθ1  c  senθ2
6
5
senθ1  senθ2
6
senθ1 6

senθ2 5
Como os ângulos de incidência e refração são menores do que 10º, a aproximação
apresentada no texto é válida e, portanto:
θ1 6
3 6
15
 
  6θ2  3.5  θ2 
θ2 5
θ2 5
6
 θ2  2,5º
Resposta
da
questão
49:
Dados apresentados:
Página 58 de 83
LISTA – UERJ – 3ª SÉRIE
p3m
o  3 mm
p '  20 mm
i
P
i
20
60
  
i 
mm
0
P
3 3000
3000
 i  0,02 mm
Resposta
da
questão
50:
[C]
Quando o fio metálico é ligado como mostrado na segunda figura, as lâmpadas L1 e L2
entram em curto circuito, apagando. A lâmpada L3 permanece acesa, com brilho mais
intenso que antes.
Resposta
da
questão
51:
Dados nominais fornecidos no enunciado:
U  200V P  60w
A partir destes dados, temos:
E  P  Δt  15.103 kω  4 h neste resistor é dada por:
P
P
U2
1002
3.10000


R  2000 
2000
 3 


30
 P  15w
2
A energia consumida em 4 horas é dada por:
E  P  Δt  15.103 kw   4 h
Página 59 de 83
LISTA – UERJ – 3ª SÉRIE
 E  0,06kwh
Resposta
da
questão
52:
[B]
Como mencionado no enunciado:
i
i1  2  i2  3.i1
3
Estando paralelas, as lâmpadas estão submetidas à mesma tensão elétrica. Analisando a
potência dissipada por cada uma temos:
P
P1  U.i1  U  1
i1
P
P2  U.i2  U  2
i2
P2 P1
  P2.i1  P1.i2
i2
i1
P2.i1  P1.3.i1
P2  P1.3
P
1
 1 
P2 3
Resposta
da
questão
53:
Como a potência de entrada é igual à de saída, temos:
ie  Ue  is  Us
Substituindo pelos valores apresentados, temos:
Página 60 de 83
LISTA – UERJ – 3ª SÉRIE
ie  120  1,2  10
 ie  0,1A
Resposta
da
questão
54:
da
questão
55:
v  λ  f  v  220.7
 v  1540 m / s
Resposta
[D]
Dados: e (módulo da carga do elétron); qd   1 e; qs  qs .
3
Se a partícula káon é eletricamente neutra, sua carga total é nula. Então a carga do quark
 
d  qd  somada à carga do antiquark s qs é nula.
1
1
1
qd  qs  0   e  qs  0  qs  e  qs   e.
3
3
3
Então a estranheza é:
S  2Q 
q
1
1
 S2 s   S2
3
e 3
1 e
3  1  3 
e
3
3
S  1.
Resposta
da
questão
56:
No movimento uniformemente variado (MUV), a velocidade média é igual a média das
velocidades. Como podemos perceber nesta questão, as velocidades médias dos móveis
A e B são iguais (executam o mesmo deslocamento escalar no mesmo intervalo de
tempo), portanto, a média das velocidades dos dois veículos também será igual. Logo:
V0A  VFA V0B  VFB

2
2
V0A  (V0A  aA .t)  V0B  (V0B  aB.t)
2.V0A  aA .t  2.V0B  aB.t
Página 61 de 83
LISTA – UERJ – 3ª SÉRIE
Conforme o enunciado, temos:
V0A  V0 

V0B  2V0 

aA  a

aB  a / 2 
Assim:
2.V0  a.t  2.(2V0 )  (a / 2).t
a
2.V0  a.t  4.V0  .t
2
at
 2V0
2
4V
t  0
a
Resposta
da
questão
57:
Analisando a sequência, podemos perceber que a cada segundo que passa a distância
percorrida aumenta em 10 metros.
ΔST  5  15  25  35
ΔST  80m
Como podemos perceber, trata-se de um movimento uniformemente variado onde a
Página 62 de 83
LISTA – UERJ – 3ª SÉRIE
velocidade média é a média das velocidades. Logo:
ΔS V0  V

Δt
2
80 0  V
VM 

4
2
 V  40 m s
VM 
Resposta
da
questão
58:
da
questão
59:
O período é dado por:
Δt 10

 0,5s
n 20
1
1
f 
 f  2Hz
T 0,5
T
Resposta
[D]
No triângulo OAB: a2  b2  262  a2  b2  676. (I)
No triângulo OAC: a2  82  h2. (II)
No triângulo ABC: b2  182  h2. (III)
Substituindo (II) e (III) em (I):
82  h2  182  h2  676  2h2  288  h2  144  h  12 m. O
trabalho da força
pela força F  WF  é numericamente igual à “área” entre a linha do gráfico e o eixo do
deslocamento.
WF 
26  12
2
 WF  156 J.
Página 63 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
60:
questão
61:
Variação da quantidade de movimento:
ΔQ  m.ΔV  forma escalar
ΔQ  0,06.(60  0)  0,06.60  3,6
 ΔQ  3,6 kg  m s
Variação da energia cinética:
ΔEC  EC.F  EC.0  m.
V2
V2
 m. 0
2
2
602
0
2
 ΔEC  108 J
ΔEC  0,06.
Resposta
da
Analisando as forças atuantes sobre a madeira que flutua no recipiente “B”, temos:
Como podemos perceber, o módulo do empuxo (E) é igual ao peso da madeira (PM),
entretanto o princípio de Arquimedes nos diz que o módulo do empuxo (E) é igual ao
pelos do líquido deslocado (PLD). Assim, podemos concluir que:
PLD  PMAD.
Assim sendo, se retirarmos a madeira e completarmos o recipiente com água, a
indicação na balança continuará a mesma, ou seja, equilibrada.
Página 64 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
62:
[D]
As figuras a seguir mostram as diferentes situações do cilindro.
Nas situações das figuras 1, 2 e 3 o fio ainda não está esticado (F = 0). Na situação da
figura 4, o fio começa a ser tracionado (H > L) e a intensidade da tração aumenta à
medida em que o nível da água sobe, pois o empuxo aumenta e o corpo permanece em
repouso. A partir da situação da figura 5, quando o cilindro já está totalmente coberto
pela água, o empuxo deixa de aumentar, permanecendo constante à força de tração no
fio (F = E – P).
Resposta
da
questão
63:
[C]
Calculemos a velocidade do cofre ao atingir o solo, considerando g  10 m/s2 .
Aplicando Torricelli:
v2  v02  2gh  v  2 10  5  v  10 m / s  36 km / h.
Inserindo esses dados na tabela e calculando as quantidades de movimento.
Página 65 de 83
LISTA – UERJ – 3ª SÉRIE
Corpos
Massa Velocidade Quantidade de movimento
(kg)
(km/h)
(kg.km/h)
120
60
Q1 = 7.200
automóvel 1100
70
Q2 = 77.000
caminhão
3600
20
Q3 = 72.000
cofre
300
36
Q4 = 10.800
leopardo
Analisando os valores obtidos, constatamos que: Q1  Q4  Q3  Q2.
Resposta
da
questão
64:
[C]
Dados: m1 = 5 kg; d1 = 15 cm; m2 = 8 kg.
Seja b a distância do ponto de suspensão do prato até o ponto de suspensão do gancho.
Como há equilíbrio de rotação, temos:

mPd1  m1gb


mPd2  m2gb
 
d1 m1

d2 m2
Resposta

15 5

 d2  24 cm.
d2 8
da
questão
65:
A lei da gravitação universal descreve que dois corpos de massas m1 e m2, cujos centros
de massa estão separados por uma distância “d”, são atraídos por uma força cujo
módulo é dado por:
FG 
G.m1.m2
d2
Onde “G” é uma constante, definida como constante universal da gravitação, cujo valor,
igual para interação entre todos os corpos, é dada por:
G  6,67.1011N.m2 / kg2
Página 66 de 83
LISTA – UERJ – 3ª SÉRIE
Como uma constante universal é igual para todos os corpos, a razão pedida tem valor
igual a 1.
Resposta
da
questão
66:
[B]
Dados: m  3,6  104 kg ; M  18 g  18  103 kg ; R  8  102 atm  L/mol ; T  227ºC  5  102 K ;
P  30 atm .
Usando a equação de Clapeyron:
PV 
m
mRT 3,6  104  8  102  5  102
RT  V 

M
MP
18  103  30

V  2,67  106 L.
Resposta
da
questão
67:
CAPACIDADES TÉRMICAS:
Cx 
Qx
80cal
80cal


Δθx (281  273)K
8K
Cx  10cal / K
Cy 
Qy
Δθy

40cal
40cal

(283  273)K 10K
Cx  4cal / K
CALORES ESPECÌFICOS SENSÌVEIS:
Cx  mx .c x  10  20.c x
c x  0,5cal / gK
Cy  my .c y  4  10.c y
c y  0,4cal / gK
Página 67 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
68:
da
questão
69:
Q
 P.Δt  m.c.Δθ
Δt
P.Δt 120  60
Δθ 

m.c
200  1
 Δθ  36C
P
Resposta
Conectando as esferas por fios condutores, haverá um rearranjo das cargas.
Considerando as esferas idênticas, a carga final de cada uma após a conexão é dada por:
Q' 
QA  QB 20  ( 4)

2
2
 Q'  8μC
Como a carga final de todas as esferas é positiva, a força entre elas será repulsiva.
Assim sendo, após a desconexão dos cabos condutores, a força resultante sobre a
partícula 3 pode ser representada pela ilustração abaixo:
Resposta
da
questão
70:
Calculando a corrente (iBAT.) antes da inserção do resistor R3:
i BAT 
E
9

Req. 2400
Assim, o resistor R2 fica submetido a uma tensão elétrica (U2) dada por:
U2  R2 .i BAT
9
U2  800.
2400
U2  3V  tensão antes da inserção de R3
Página 68 de 83
LISTA – UERJ – 3ª SÉRIE
Segundo o enunciado, a inserção do resistor R3 em paralelo com o resistor R2 resultou
em uma redução na tensão elétrica no resistor R2 para 1/3 do valor inicial. Chamando de
U2’ a tensão elétrica que o resistor R2 ficou submetido após a inserção do resistor R3,
temos:
U
U2 '  2  1 V  tensão após a inserção de R3
3
Assim sendo, o resistor R1 fica agora submetido a uma tensão (U1’) de 8V, o que
possibilita calcularmos a corrente que atravessa a bateria após a inserção de R3
(chamaremos de iBAT’).
U1'  R1.iBAT '
8  1600.iBAT '
8
1

1600 200
1
i BAT ' 
A
200
i BAT ' 
Utilizando a lei de Pouillet, podemos agora calcular a nova resistência equivalente do
circuito (Req.’):
i BAT ' 
E
Req. '
1
9

200 Req. '
 Req. '  1800Ω
Resposta
da
questão
71:
[A]
Dados: PV = 1.000 W; PI = 2.000 W; U = 120 V;
Da expressão da potência elétrica:
Página 69 de 83
LISTA – UERJ – 3ª SÉRIE

U2
R


I
PI
U2
U2

P
 R

R
P
U2

R

V

PV

RI 1.000

 0,5.
RV 2.000
Resposta
 
da
RI U2 PV


RV
PI U2

RI PV

RV
PI

questão
72:
questão
73:
questão
74:
[C]
(P)max  Vi  120x10  1200 W
N
Pmax
1200

 20
Plâmpada
60
Resposta
da
[A]
P
V2
120 2
14400
 8  60 
R 
 30Ω
R
R
480
Resposta
da
[C]
Os movimentos horizontais são uniformes. Portanto, o maior alcance será o da bola com
maior velocidade inicial.
Resposta
da
questão
75:
[D]
O movimento de queda das bolas é acelerado com a gravidade. Os tempos de queda são
iguais.
Resposta
da
questão
76:
[A]
Página 70 de 83
LISTA – UERJ – 3ª SÉRIE
Observação: no enunciado, as forças deveriam levar o símbolo de vetor, pois, sem ele,
refere-se apenas ao módulo da força e módulo não tem direção. O correto é:
 Fp : força paralela ao solo exercida pela pessoa;
 Fa : força de atrito exercida pelo piso.
A caixa se desloca na mesma direção e sentido de Fp .
A força que a caixa exerce sobre a pessoa é FC .
A força que a pessoa aplica na caixa Fp  e a que a caixa aplica na pessoa FC  formam
um par ação-reação, tendo, portanto, a mesma intensidade: Fp  FC .
Como o movimento é retilíneo e uniforme, as forças que agem sobre a caixa estão
equilibradas, ou seja: Fp  Fa . Assim: Fp  FC  Fa
Resposta
da
questão
77:
[C]
A força que a pessoa aplica na caixa Fp  e a que a caixa aplica na pessoa FC  formam
um par ação-reação, tendo, portanto, a mesma intensidade: Fp  Fc .
Como o movimento é retilíneo e acelerado, a força que a pessoa aplica na caixa tem
intensidade maior que a da força de atrito, ou seja: Fp  Fa .
Assim: Fp  Fc  Fa
Resposta
da
questão
78:
t1 = 3 s  S1 = 28 m; t2 = 8 s  S2 = 58 m.
Calculando a velocidade:
v
S 58  28 30


 v  6 m/s.
t
83
5
Calculando a posição inicial A (no instante t = 0):
v
28  SA
S
 6
 28  SA  18  SA = 28 – 18  SA = 10 m
t
30
Página 71 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
79:
[C]
Por inércia, quando o copo é abandonado, ele continua com a mesma velocidade
horizontal em relação à Terra, ganhando apenas velocidade vertical devido à gravidade.
Assim, o copo está em repouso em relação ao piso do avião, portanto ele cai próximo ao
ponto R, como se o avião estivesse em repouso em relação ao solo.
Resposta
da
questão
80:
Dados: m = 6,0 kg; v1 = 0,4 m/s; t = (1,5 – 0,5) = 1 s; F = 12,0 N.
1ª Solução:
Considerando que a força dada seja a resultante e que o movimento seja retilíneo, do
Princípio Fundamental da Dinâmica (2ª Lei de Newton), temos:
F = m a  12 = 6 a  a = 2 m/s2.
a
v
v  0,4
 2
 v  2  0,4  v = 2,4 m/s.
t
1
2ª Solução:
Considerando que a força dada seja a resultante e que o movimento seja retilíneo, do
Teorema do Impulso, temos:
F t = m v  v 
F t
12(1)
 v = 2 + 0,4  v = 2,4 m/s.
 v  0,4 
m
6
Resposta
da
questão
81:
OBS: a questão ficaria melhor, se o examinador pedisse na última linha do enunciado:
“Estime o módulo da aceleração do patinador após ter cessado o empurrão.” Também
deveriam estar especificadas as características da trajetória (retilínea / curvilínea;
horizontal / inclinada).
Dados: P = 800 N; Fat = 40 N; g = 10 m/s2.
Página 72 de 83
LISTA – UERJ – 3ª SÉRIE
Da expressão do Peso:
P = m g  800 = m (10)  m = 80 kg.
Supondo que a trajetória seja retilínea e horizontal, após o empurrão, a resultante das
forças sobre o patinador é a componente de atrito. Pelo Princípio Fundamental da
Dinâmica:
Fat = m a  40 = 80 a  a = 0,5 m/s2.
Resposta
da
questão
82:
[D]
Dados: F = 4 N; d = 1 m;  = 60°
O trabalho de força constante é calculado pela expressão:
T = F d cos .
Essa expressão mostra que o trabalho (T) de força constante é diretamente proporcional
ao deslocamento (d); portanto, o gráfico T = f (d) é uma reta que passa pela origem.
Para os valores fornecidos:
T = 4 (1) cos 60° = 4 (0,5)  T = 2 J.
Resposta
da
questão
83:
[A]
Calor é uma forma de energia, e a unidade de energia no SI é o joule (J).
Resposta
da
questão
84:
[B]
Dado:
P
 12,5.
E
Do princípio fundamental da dinâmica, vem:
Página 73 de 83
LISTA – UERJ – 3ª SÉRIE
P – E = m a  m g – E = m a.
mg
P
P
 12,5  E 

.
E
12,5 12,5
Mas:
Substituindo na expressão anterior:
m g
10 –
mg
2
 m a . Considerando g = 10 m/s :
12,5
10
= a  a = 10 – 0,8  a = 9,2 m/s2.
12,5
Resposta
da
questão
85:
Dados:
M = 50 kg  PC = PM = 500 N; m = 10 kg  Q = 100 N; g = 10 m/s2; AB = 2 m 
MB = 1 m.
Uma pessoa permanece em M, ponto médio da prancha; a outra pode deslocar-se, no
máximo, até o ponto C, quando a prancha está na iminência de tombar. Nessa situação,
a normal de contato entre a prancha e o apoio A é nula.
Em relação ao ponto B, o somatório dos momentos horários é igual ao somatório dos
momentos anti-horários.
MPC  MPM  MQ  PC x = (PM + Q) 1  500 x = (500 + 100) 1  x 
600
 x = 1,2 m.
500
Mas, da figura:
d = 1 + x  d = 1 + 1,2  d = 2,2 m.
Resposta
da
questão
86:
[B]
Página 74 de 83
LISTA – UERJ – 3ª SÉRIE
OBS: se a pressão do ar no interior da bola é de 1 atm a bola está “vazia” ou “murcha”.
Quando se diz que a bola está sob pressão de 1 atm, refere-se à pressão manométrica, ou
seja, acima da pressão atmosférica. Portanto, no caso, a pressão no interior da bola é de
2 atm. No entanto, resolvamos com os dados fornecidos.
Dados: D = 20 cm  R = 10 cm = 1 dm; p = 1 atm; T = 27 °C = 300 K; M = 30 g/mol;
R = 0,08 atm·L/mol·K;  = 3.
Calculando o volume da bola:
V=
4 3 4
3
R  (3)(1)3  V = 4 dm = 4 L.
3
3
Da equação de Clapeyron:



30 g
 1 atm  4  L 
mol
Mp V
m
120

pV = RT  m =
 m

M
RT
0,08 atm  L
 300  K  24
mol  K

m = 5 g.
Resposta
da
questão
87:
questão
88:
Dados:
P0  2 atm

T  27 °C  300 K
Inicial  0
V0
n
 0
P  ?
T  7 °C  280 K

Final V0  V

n  n0

2
Da equação geral dos gases ideais:
P V P0 V0

n T n0 T0

P
2

n0
n0  300 
 280
2
 P
280
300

P = 0,93 atm.
Resposta
da
Dados: nA = 1,0; nB = 1,2; sen 7° = 0,12.
Página 75 de 83
LISTA – UERJ – 3ª SÉRIE
A figura a seguir ilustra a situação. Como o raio refratado incide no espelho passando
pelo foco, ele reflete paralelo ao eixo principal.
Sabemos que quando um ângulo é pequeno ( < 10°), podemos fazer a aproximação:
sen  = tg  = (radiano).
Como nesse caso i = 7° e r < i (ângulos pequenos), podemos então trocar o seno pela
tangente na lei de Snel. Assim:
nA tg i = nB tg r  1 (0,12) = 1,2 tg r  tg r =
0,12
 tg r = 0,1.
1,2
Mas no triângulo OPB destacado na figura:
tg r =
d
d
 0,1 =  d = 0,3 m = 30 cm.
3
3
Resposta
da
questão
89:
Dados: V = 600 V; E = 200 V/m; k = 9  109 N.m2/C2.
Como o Potencial elétrico é positivo, a carga é positiva. Então, abandonando os
módulos, temos:
kQ
r
kQ
E 2
r
V

V kQ r 2
V
600



r  r 
 r = 3 m.
E
r kQ
E
200
Página 76 de 83
LISTA – UERJ – 3ª SÉRIE
Substituindo na expressão do Potencial:
V
r V 3  600
kQ
 Q

 200  109
r
k
9  109

Q = 2  10–7 C.
Resposta
da
questão
90:
[D]
Os valores das resistências formam uma PG de razão
1
.
2
Seja:
a = x. Então:
b=
x
2
e c=
x
4
A resistência equivalente do circuito é:
1
1 1 1
1
1 1
1
1
1 2 4 7
  

 

    .

x
Req a b c
Req x x
Req x x x x
2
4
Como Req = 2 Ω , temos:
1 7

 x = 14 Ω .
2 x
Assim,
a + b + c = 14 +
Resposta
14 14

 14  7  3,5  a + b + c = 24,5 Ω .
2
4
da
questão
91:
Página 77 de 83
LISTA – UERJ – 3ª SÉRIE
Dados: UCD = UBE = 18 V; i2 = 4,5 A.
1ª Solução:
No resistor R3:
UCD = R3 i3  18 = 12 i3  i3 = 1,5 A.
A corrente total é:
i = i2 + i3 = 4,5 + 1,5  i = 6 A.
Aplicando a Lei de Kirchoff na malha ABCDEFA:
E – R1 i – UCD – R4 i = 0  E = 3 (6) + 18 + 4 (6)  E = 60 V.
2ª Solução:
No resistor R3:
UCD = R3 i3  18 = 12 i3  i3 = 1,5 A.
No resistor R2:
UBE = R2 i2  18 = R2 (4,5)  R2 = 4 Ω .
A corrente total é:
i = i2 + i3 = 4,5 + 1,5  i = 6 A.
Calculando a resistência equivalente do circuito:
Req = R1 
R2  R3
12  4
 R4  Req  3 
 4  Req = 10 .
R2  R3
12  4
Aplicando a Lei de Ohm-Pouillet:
Página 78 de 83
LISTA – UERJ – 3ª SÉRIE
E = Req i  E = 10 (6)  E = 60 V.
Resposta
da
questão
92:
[D]
Dados: U = 12 V; i = 100 A; t = 1 min = 60 s.
Da relação entre potência elétrica e energia:
E = P t = U i t = (12) (100) (60) = 72.000 J = 7,2  104 J.
Resposta
da
questão
93:
questão
94:
Dados: v = 1.188km/h = 330 m/s; f = 2.640 Hz.
Da equação fundamental da ondulatória:
v f


v
330

f 2.640
Resposta
Dados: Qp = e; Qu =

  0,125 m.
da
2
e.
3
Calculando a carga do quark down:
2
1
4
Qp = 2 Qu + Qd  e = 2  e  + Qd  e = e + Qd  Qd =  e .
3
3
3


Consideremos que o nêutron seja formado de x quarks up e y quarks down. Como sua
carga é nula, temos:
x + y = 3

 1 
 2 
 x  3 e  + y   3 e  = 0  2x  y  0



 

y = 2x.
Então:
x + 2x = 3  x = 1  y = 2.
Portanto, o nêutron é formado de 1 quark up e 2 quarks down. (n = udd).
Resposta
da
questão
95:
Página 79 de 83
LISTA – UERJ – 3ª SÉRIE
[C]
Como se trata de um lançamento horizontal, o tempo de queda é o mesmo do tempo de
queda da queda livre:
h
1 2
2h
2(1)
20 4,5
 t = 0,45 s.
gt  t 



2
g
10
10
10
Resposta
da
questão
96:
[B]
Se a velocidade relativa ao vagão é a mesma, o alcance horizontal relativo ao vagão
também é o mesmo, ou seja, 5 m.
Resposta
da
questão
97:
[C]
Dado: m = 20 kg.
A figura mostra as forças agindo sobre o corpo que desce o plano inclinado.
Aplicando Pitágoras: (CF)2 + (CB)2 = (FB)2  62 + 82 = (FB)2  (FB) = 10 m.
Se o bloco desce com velocidade constante, a resultante das forças sobre ele é nula.
Assim, a intensidade da força de atrito (Fat) é igual à da componente tangencial do peso
(Pt) :
6
Fat = Pt = P sen  = m g  CF  = (20) (10)    Fat = 120 N.
 FB 
 10 
Página 80 de 83
LISTA – UERJ – 3ª SÉRIE
Resposta
da
questão
98:
[D]
Seja P o peso dos corpos.
F1  P  sen   P 
6 3P

.
10 5
Como AF é diagonal do paralelepípedo, segue que
AF  62  82  152  325  5 13.
Logo,
F2  P  sen   P 
6
6P

.
5 13 5 13
Portanto,
Página 81 de 83
LISTA – UERJ – 3ª SÉRIE
3P
F1
13
 5 
.
6P
F2
2
5 13
Resposta
da
questão
99:
[B]
A velocidade do foguete (vf) é 4 vezes a velocidade do avião (va)  vf = 4 va
Equacionando os dois movimentos uniformes, com origem no ponto onde está o foguete
no instante t1:
Sf = vf t  Sf = 4 va t e Sa = 4 + va t.
Igualando as funções horárias para instante de alcance (t2):
Sf = Sa  4 va t2 = 4 + va t2  3 va t2 = 4  t2 =
4
.
3v a
Substituindo:
 4
 3v a
Sf = 4 va 
Resposta

16
km = 5,3 km .
  Sf =
3

da
questão
100:
[D]
Página 82 de 83
LISTA – UERJ – 3ª SÉRIE
Para simplificar a parte algébrica, façamos CD = L e AB = h
Assim:
h
3
3

h
L
L 10
10
A área (S) do hexágono é dada por: S =
3 3 2
L . O volume da piscina é o produto da área
2
do hexágono (S) pela profundidade (h): V =
3 3 2
3 3 2 3
(L) (h)  V =
(L) ( L)  450 =
2
2
10
9 3
3
L  L = 1000  L = 10 m.
20
A figura abaixo mostra a trajetória AM seguida pelo atleta.
Como se trata de um hexágono, AD = 2(L) = 20 m e MD =
L
= 5 m.
2
A distância percorrida pelo atleta (d) pode ser calculada no triângulo destacado, usando
a lei dos cossenos:
d2 = 52 + 202 – 2(5)(20)cos 60°  d2 = 25 + 400 – 100 = 325  d = 325  18,1 m.
Sendo, v = 1 m/s, temos: d = v t  18,1 = 1t  t = 18,1 s.
Página 83 de 83