o ensino de cálculo diferencial e integral em um curso de

O ENSINO DE CÁLCULO DIFERENCIAL E INTEGRAL EM UM
CURSO DE ADMINISTRAÇÃO: PRINCIPAIS DIFICULDADES DE
APRENDIZAGEM DOS ALUNOS
Sabrina Anne de Lima – [email protected]
Universidade Tecnológica Federal do Paraná
Ponta Grossa – Paraná
Sani de Carvalho Rutz da Silva - [email protected]
Universidade Tecnológica Federal do Paraná
Ponta Grossa – Paraná
Guataçara dos Santos Junior – [email protected]
Universidade Tecnológica Federal do Paraná
Ponta Grossa – Paraná
Marina Ferreira Araujo de Almeida – [email protected]
Universidade Tecnológica Federal do Paraná
Ponta Grossa – Paraná
Resumo:O ensino de Cálculo Diferencial e Integral está vinculado a diversos cursos de
graduação, principalmente naqueles ligados à área de Exatas e Engenharias. Porém alguns
cursos da área de Sociais Aplicadas, também se utilizam de conceitos desta disciplina em
seus ementários. É o caso do curso de Administração que utiliza conceitos de Cálculo com o
intuito de desenvolver em seus alunos capacidade de raciocínio matemático e lógico a ser
aplicado em diversas situações. O objetivo deste artigo é verificar as principais dificuldades
de aprendizagem de alunos de um curso de Administração em disciplina relacionada ao
Cálculo, de uma universidade do interior do Paraná. Os alunos foram submetidos a um
questionário, predefinido, de modo a tentar perceber se havia reais dificuldades e investigar
os principais fatores que limitam a aprendizagem da disciplina. Os resultados encontrados
foram sintetizados em gráficos para melhor análise. Percebeu-se a real dificuldade dos
alunos na aprendizagem da disciplina, bem como a necessidade que os próprios discentes
veem de uma disciplina preliminar que os auxilie com conteúdos de matemática básica.
Palavras chave: Ensino, Aprendizagem, Cálculo Diferencial e Integral, Curso de
Administração.
1 INTRODUÇÃO
O Cálculo Diferencial e Integral (ou simplesmente Cálculo) apesar de sua importância e
aplicabilidade em diversas áreas do conhecimento é visto pelos alunos, como uma disciplina
de difícil entendimento e cujo número de reprovações ainda é um fator que incomoda.
Diversos são os fatores que podem ser atribuídos ao fracasso no ensino e aprendizagem
de disciplinas que envolvem o Cálculo, o que parece tornar a não aprovação uma ocorrência
comum e aceitável.
Por ser uma disciplina presente em diversos cursos de graduação, principalmente os da
área de Exatas e Engenharias, pesquisas que buscam entender as dificuldades dos alunos são
comuns.
Porém, não somente estas áreas se utilizam de disciplinas de Cálculo em seus ementários.
Alguns cursos da área de Ciências Sociais Aplicadas, como é o caso do curso de
Administração, também apresentam algumas matérias que trazem conceitos e definições de
Cálculo Diferencial e Integral.
Se para alunos de áreas específicas da Matemática o ensino e aprendizagem de cálculo é
um fator temente, o que esperar, então, para alunos de outras áreas?
Para perceber estas dificuldades, este estudo tenta apontar as principais causas e
dificuldades na aprendizagem de Cálculo Diferencial e Integral I para alunos de um curso de
Administração de uma universidade pública no interior do estado do Paraná.
2 REFERENCIAL TEÓRICO
O Cálculo Diferencial e Integral (ou simplesmente Cálculo) é o ramo da Matemática que
estuda as variações das grandezas e acumulação de quantidades, presente, principalmente, no
estudo dos movimentos.
De acordo com Swokowski (1994), foi descoberto por volta do século XVII com a
finalidade de explorar problemas relacionados ao movimento, uma vez que os pressupostos da
álgebra e da trigonometria não eram suficientes para esclarecer questões relacionadas a
movimentos não regulares.
Os antigos gregos já se utilizavam de conceitos de limites para derivar resultados finitos.
Acredita-se que Arquimedes de Siracusa (287-212 a.C), foi um dos pioneiros na utilização de
conceitos de limite com a finalidade de calcular área e volume de figuras planas e sólidas.
(BATISTA, 2010).
Esta utilização surgiu a partir do Método da Exaustão de Eudoxo, principio que acabou
por ser conhecido como Paradoxo de Arquimedes. Este axioma foi postulado por Euclides da
seguinte forma: Se de uma grandeza qualquer se subtrai uma parte não menor que sua metade
e do resto novamente subtrai-se uma parte não menor que sua metade, e assim por diante, se
chegará por fim a uma grandeza menor que qualquer outra predeterminada da mesma
espécie.(BOYER, 1996).
Desde sua consolidação com Leibniz e Newton é considerado como indispensável para
a formação do pensamento em diversas áreas do conhecimento, principalmente as que tratam
de disciplinas de cursos de graduação voltados para a área de ciências exatas. (COXE, 2013).
Apesar de sua importância no currículo de alguns cursos superiores, disciplinas que
abordam Cálculo Diferencial e Integral I, acabam se tornando um desafio para os estudantes,
que vão revelando, turma a turma, as dificuldades encontradas, nem sempre de maneira
totalmente verídica, aumentando ainda mais o mito de uma disciplina complexa e difícil.
(MELLO, et al, 2001). Esta perspectiva em relação ao Cálculo reflete no número de
reprovações nas disciplinas a ele relacionadas.
De acordo com Barreto (1995) parte deste fracasso se deve à má formação durante a
educação básica, fruto de turmas com alunos passivos, sem conhecimento de conceitos
básicos, desabituados a estudar e, como consequência, inseguros. Mas esta não é a única
justificativa.
Alguns alunos atribuem este fato ao nível de abstração que a matéria exige e a
metodologia adotada pelo professor.(SANTOS, MATOS, 2012).
Outros ainda atribuem o fracasso na aprendizagem de cálculo na falta de habilidade dos
alunos em construir e compreender conceitos, reconhecendo quando aplicá-los e percebendo o
alcance e restrições destas aplicações, isto é, o fato de o aluno conseguir perceber a lógica
simbólica para resolver determinadas questões não significa a compreensão do conceito
aplicado. (BARROS, MELONI, 2006).
Outros alunos ainda acreditam que parte das dificuldades esteja inserida na estrutura de
ensino, isto é, na forma em que o docente conduz sua prática pedagógica. (WROBEL, et.al,
2013).
De acordo com Souza (2001) as aplicações do Cálculo Diferencial e Integral podem ser
vistas em grande parte dos problemas mensuráveis, estendendo seu uso desde a Física até
Economia e Administração.
De forma geral, disciplinas relacionadas ao Cálculo estão contempladas em cursos de
engenharia, tecnologias e algumas licenciaturas, que necessitam de conceitos destas
disciplinas para a realização futura de tarefas de grande complexidade e que facilite a
assimilação de outros conteúdos. (SILVA, et.al, 2010).
Porém, não somente cursos da área de Exatas apresentam conceitos de Cálculo
Diferencial e Integral em seus ementários. O curso de Administração se utiliza de conceitos
de Cálculo Diferencial e Integral a fim de desenvolver em seus acadêmicos a capacidade de
raciocínio matemático. Essa recomendação vem do Ministério da Educação que coloca em os
conteúdos que devem ser abordados em disciplinas relacionadas à área de Matemática.
O ementário básico deve conter, dentre outros tópicos, Conjuntos e Subconjuntos,
Limites e Continuidade, Diferenciação e Integração (BRASIL, 2004).
As Diretrizes Curriculares Nacionais dos Cursos de Graduação, disponível no parecer
CES/CNE 0146/2002, estabelece que o graduado em administração deve apresentar dentre
suas habilidades e competências:
“IV - desenvolver raciocínio lógico, crítico e analítico para operar com
valores e formulações matemáticas presentes nas relações formais e
causais entre fenômenos produtivos, administrativos e de controle, bem
assim expressando-se de modo crítico e criativo diante dos diferentes
contextos organizacionais e sociais”; (BRASIL, 2002, p.41).
Além disso, os cursos de graduação em Administração devem contemplar em seus
currículos conteúdos de “Estudos Quantitativos e suas tecnologias, (...), Pesquisa Operacional,
Teoria dos Jogos, Modelos Matemáticos e Estatísticos (...)” (BRASIL, 2002).
Verifica-se assim a necessidade de conteúdos matemáticos para cursos de Administração
de Empresas para que o profissional formado seja capaz de atender as perspectivas do
mercado de trabalho.
De acordo com o Ministério da Educação (MEC), no Estado do Paraná 163 municípios
possuem Instituições de Ensino Superior (IES) que oferecem o curso de Administração em
165 IES diferentes, sendo 144 Instituições com curso presencial e 28 com cursos à distância
(EAD). (BRASIL, 2014)
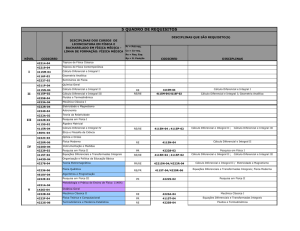
O quadro 1 mostra alguns exemplos de IES do Paraná que abrangem conteúdos de
Cálculo Diferencial e Integral em cursos de Administração para Cursos Cadastrados pelo
Ministério da Educação (MEC), segundo informações do portal e-mec.
Quadro 1 - Relação de IES do Estado do Paraná e tópicos de Cálculo trabalhados para Cursos
de Administração
INSTITUIÇÃO
SIGLA
NOME DA
DISCIPLINA
TÓPICOS
TRABALHADOS
PERÍODO(S)
TRABALHADO(S)
Centro
Universitário de
Maringá
UNICESUMAR
Matemática
Noções básicas de
cálculo
1º período
Faculdade
Arthur Thomas
CESA
Faculdade
Maringá
CESPAR
Faculdade
Paranaense
FACCAR
Faculdades
Integradas do
Vale do Ivai
Pontifícia
Universidade
Católica do
Paraná
Universidade
Estadual de
Londrina
Matemática
Matemática
Aplicada à
Administração
Matemática
para
Administração
Matemática
Básica;
UNIVALE
Matemática
Aplicada
Funções;
Limites;
Derivadas
Números Reais;
Funções.
Funções;
Limites;
Derivadas;
Diferenciais;
Integrais
1º período
1º semestre
1ª série
1º semestre
2º semestre
PUCPR
Matemática
Aplicada a
Negócios
Conjuntos;
Funções;
Limites;
Derivadas
2º Semestre
UEL
Matemática
para
Administração
Limites;
Derivadas.
2º Semestre
Universidade
Estadual de
Maringá
UEM
Matemática II
Universidade
Estadual de
Ponta Grossa
UEPG
Métodos
Quantitativos I
Universidade
Federal do
Paraná
UFPR
Complementos
de Matemática
I
UTFPR
Matemática
Aplicada a
Administração
Universidade
Tecnológica
Federal do
Paraná
Funções;
Limites;
Derivadas;
Integrais
Conjuntos;
Funções.
Estudo de Cálculo
Diferencial e
Integral de funções
reais.
Conjuntos;
Funções;
Limites;
Derivadas;
Integrais
Conjuntos;
Funções;
Limites;
Derivadas;
Integrais.
Funções;
Limites;
Derivadas;
Integrais
2º Semestre
1º Período (ano)
2º Semestre
1º ano
INSTITUIÇÃO
SIGLA
Universidade
Tuiuti do Paraná
UTP
NOME DA
DISCIPLINA
Matemática
Aplicada
TÓPICOS
TRABALHADOS
Derivadas;
Integrais
PERÍODO(S)
TRABALHADO(S)
1º semestre
Fonte: os próprios autores
Percebe-se assim que disciplinas relacionadas ao Cálculo Diferencial e Integral estão
presentes na grade curricular dos cursos de Administração em diversas instituições de ensino.
Ao analisar uma dessas disciplinas em um curso de Administração de uma IES do interior
do Paraná, pode-se perceber a dificuldade dos alunos em realizar a disciplina, bem como
perceber que, em anos anteriores, o número de reprovações para esta matéria foi considerável.
Isso induz o Departamento do curso a oferecer, todos os anos, turmas especiais destinadas
somente a alunos que reprovaram na disciplina.
Segundo Nascimento (2000), a matéria de Calculo Diferencial e Integral, presente nos
mais diversos cursos de graduação, apresenta um número considerável de reprovações. Este
índice de reprovações é menor nos cursos de Engenharia e maior nas demais áreas,
sustentando a relação inversa com a afinidade do aluno, peculiaridade da opção da carreira.
É possível perceber assim, uma das causas que justifica o número de reprovações na
disciplina de Cálculo para o curso de Administração. Esta porém, não é a única explicação.
Tentando verificar as possíveis causas de reprovação na disciplina, bem como as
principais dificuldades encontradas (do ponto de vista dos alunos), realizou-se uma pesquisa
em uma turma de 1º período do curso de Administração de uma Universidade pública do
interior do Paraná. Este estudo foi realizado com 29 alunos desta turma que foram submetidos
ao um questionário. Para a primeira metade da disciplina, apenas 7 (17,5%) alunos desta
turma atingiram a média proposta pela IES.
A disciplina é oferecida na modalidade anual, com 68h/a de carga horária total e 2 aulas
semanais. A ementa exige o ensino de conjuntos, funções, limites, derivadas e integrais. Em
face disso, os alunos foram submetidos a um questionário com o objetivo de identificar as
principais dificuldades da turma na aprendizagem da disciplina.
3 ANÁLISE DE RESULTADOS
Os alunos, objetos deste estudo, foram submetidos a um questionário com a finalidade de
perceber qual seriam as dificuldades na aprendizagem de uma disciplina que envolve
conceitos de Cálculo Diferencial e Integral.
Este questionário continha duas perguntas relacionadas à aprendizagem de Cálculo, sendo
a primeira com cinco opções de resposta e a segunda com nove opções de resposta.
1)
Você percebe que tem dificuldades na aprendizagem de Cálculo:
Sempre
Quase sempre
Às vezes
Raramente
Nunca
Para esta pergunta, as respostas constam no gráfico 1 a seguir:
Gráfico 1 – Percepção dos aluno em relação a dificuldades na aprendizagem de Cálculo:
Pode-se perceber que 9 alunos (31,03%) dos alunos têm dificuldades na aprendizagem
“Sempre”, 8 alunos (27,59%) têm dificuldade “Quase sempre” e 12 alunos (41,38%) têm
dificuldade “Às vezes”. Nenhum dos alunos respondeu que “Raramente” tem dificuldade ou
“Nunca” tem dificuldade.
Percebe-se, então que os alunos têm dificuldades de aprendizagem na disciplina, o que
sugeriu a pergunta 2, com o objetivo de perceber qual é o fator que, na opinião dos alunos,
sugere esta dificuldade.
A pergunta 2 segue:
2)
Qual é, em sua opinião, o fator que mais dificulta a aprendizagem de
Cálculo?
A concepção de alunos e professores de considerar normal a reprovação e o
fracasso nessa disciplina. (1)
A falta de objetividade de concursos vestibulares ou exames de admissão em
cursos superiores. (2)
A grande quantidade de novos conceitos trazidos pela disciplina. (3)
A disciplina não é interessante. (4)
Falta de domínio de conteúdos básicos de matemática para cursar a disciplina, por
parte dos alunos. (5)
Falta de diversificação de metodologias adotadas. (6)
Dificuldade em perceber a aplicabilidade na área de atuação do curso. (7)
Necessidade de uma matéria preliminar que ofereça subsídios para a realização
desta disciplina. (8)
O tempo destinado
é pouco comparado
a serem aprendidos. (9)
para
com
a
o
disciplina (número de horas aula)
grande número de novos conceitos
O gráfico 2 a seguir, sintetiza as respostas dos alunos. Os números de 1 a 9 representam
os nove fatores que foram elencados para esta questão, de acordo com a sequencia
apresentada anteriormente.
Para esta pergunta, os alunos podiam marcar mais de uma alternativa, além de sugerir
novos fatores.
Gráfico 2 – Fator que mais dificulta a aprendizagem de Cálculo
Percebe-se pelo gráfico, que 18,99% das respostas sugerem o fator 5, isto é, “Falta de
domínio de conteúdos básicos de matemática para cursar a disciplina, por parte dos alunos”.
Segundo Santos e Carneiro (2013) o conhecimento matemático é naturalmente intrínseco
e cumulativo, de forma que ao desconhecer noções elementares, o aluno pode ser impedido ou
ter sua compreensão dificultada para conhecimentos posteriores. Desta forma, é necessário
que seja dada maior importância a conceitos de Matemática básica, visto que servem de prérequisito para disciplinas que se utilizem de tais ideias.
Em segundo lugar fica o fator 9 que trata do tempo destinado à disciplina. Segundo a
pesquisa 17,72% das respostas aponta que esse é um item determinante, uma vez que, para
esta turma, são ministradas apenas 2 aulas semanais, num total de 68h/aula no período.
Silva, et al (2010) afirma que os alunos possuem dificuldade em compreender os novos
conceitos aplicados ao Cálculo, uma vez que estes foram construídos e elaborados durante
milhares de anos e precisam ser assimilados pelos alunos, em apenas algumas horas do curso.
Isso faz com que a assimilação por parte dos estudantes não seja satisfatória.
Lacaz, et al (2007) afirma ainda que o tempo a ser destinado a cada tópico deve ser
colocado em concordância com a importância do assunto, explorando materiais didáticos e
tecnologias que facilitem a aprendizagem.
Com 16,46% das respostas o item “Necessidade de uma matéria preliminar que ofereça
subsídios para a realização desta disciplina” foi o terceiro item mais citado.
Este item se enquadra também na necessidade de conteúdos preliminares de matemática
básica, conforme o primeiro fator mais citado.
O quarto fator mais citado foi “A grande quantidade de novos conceitos trazidos pela
disciplina” (fator 3).
Além disso, 10,13% consideram a disciplina difícil por não perceber aplicabilidade na
área de atuação do curso.
Para completar os fatores ainda tem-se 7,59% das respostas considerando que seria
necessário diversificar as metodologias adotadas, 6,33% consideram que o vestibular (ou
outros exames de admissão à Universidade) não é suficientemente objetivo para selecionar os
alunos que dominem conteúdos de matemática.
Segundo Irias, et al, (2011), algumas reprovações podem estar relacionadas à
metodologia do professor que buscam cumprir a ementa da disciplina em um curto período de
tempo destinado para esta finalidade.
De acordo com Frescki e Pigatto (2009), a metodologia utilizada em sala de aula é, na
maior parte do tempo expositiva e dialogada o que faz com que os alunos não se
comprometam a criar hábitos de estudo que sugiram a autonomia de seu aprendizado.
O conteúdo expresso de forma mecânica e sem mostrar aplicabilidade na área de
conhecimento do aluno gera desinteresse e dificuldades na compreensão e aprendizado de
conceitos de Cálculo. (SILVA, et al, 2010)
Outros alunos ainda consideram a disciplina desinteressante (5,06%) e 2,53% acreditam
que o fato de alunos e professores acreditarem que o mito de que seja normal a reprovação na
disciplina é um fator a ser considerado.
De acordo com D’Ambrósio (2002), a matemática que predomina nos programas de
Cálculo é, normalmente, desinteressante, antiquada e sem utilidade para a realidade atual dos
estudantes, gerando baixo rendimento na disciplina.
Alguns alunos ainda sugeriram outros fatores que podem identificar a dificuldade de
aprendizagem. Para preservar a identidade dos alunos, estes foram identificados como Aluno
A, Aluno B e Aluno C.
A seguir, foram expostas as respostas de alguns alunos da turma:
Aluno A: “Entrei no curso com base fraca”.
Aluno B: “Acredito, que, também pelo fato de não ter tido uma base de tudo o que
estamos aprendendo. São poucos os alunos que conseguem resgatar isso do ensino
médio, até porque eu estudei em escola pública e não tive um professor que ensinou
bem a disciplina de cálculo/etc”.
Aluno C: “(...) tenho muita dificuldade...na última prova achei que tinha ido bem, mas
tirei 3. Matemática não é para mim...”.
Observa-se pelas colocações dos alunos e pelas respostas objetivas que a maior
dificuldade de aprendizagem dos alunos é a falta de domínio de conteúdos básicos que
auxiliem no entendimento da disciplina.
Esta percepção é exposta por Raad (2012, p. 14), ao relatar sua visão, como professor, em
relação a seus alunos:
“(...) venho observando um número crescente de alunos com dificuldades
em conteúdos básicos de Matemática. Fatorar uma expressão algébrica,
efetuar um mínimo múltiplo comum, calcular uma porcentagem, resolver
uma regra de três, reconhecer propriedades básicas da geometria
euclidiana, ler e interpretar exercícios um pouco mais extensos em sua
formulação são obstáculos que constato dentre inúmeros outros nos Cursos
de Cálculo Diferencial e Integral que ministro (...)”
Jesus, et al (2011), também afirma esta questão ao se referir à sua pesquisa, feita em duas
instituições de ensino superior. O autor percebeu que os alunos não dominavam conceitos
básicos como operações com frações, expressões algébricas, entre outras.
Percebe-se assim a necessidade de uma formação básica em matemática, proporcionada
por conteúdos de revisão e aprimoramento dos conceitos elementares. Cabe então a cada
curso perceber esta necessidade e a melhor maneira de oferecer este “reforço” de noções
matemáticas, como uma disciplina preliminar obrigatória, ou o aumento do número de aulas
para que esta revisão seja feito dentro da própria disciplina ofertada.
4 CONSIDERAÇÕES FINAIS
É de senso comum que alunos dos mais diversos cursos de ensino superior apresentam
dificuldades na aprendizagem de Cálculo, mesmo sendo para faculdades direcionadas para a
área de Exatas.
Quando se trabalha, então, com outras áreas como Ciências Sociais, como é o caso do
curso de Administração, esta dificuldade parece ainda mais aflorada, uma vez que não se trata
de uma disciplina especifica do curso ou da área de atuação profissional do acadêmico.
De acordo com a pesquisa realizada, é possível perceber que, de acordo com a visão dos
alunos, o fator que mais implica na “não aprendizagem” é a falta de domínio de conteúdos
básicos de matemática. Isso faz com que os alunos não tenham subsídios suficientes para
compreender conceitos relacionados ao Cálculo, ou desenvolver exercícios que necessitem de
tais conceitos.
O ideal, segundo os próprios alunos questionados, seria a aplicação de uma disciplina
preliminar que abrangesse e abordasse conteúdos básicos de matemática que sirvam como
alicerce para a realização da disciplina.
Seria interessante aplicar este recurso e posteriormente realizar novamente a pesquisa
sugerida para conflitar os dados e perceber se houve ou não melhora significativa na
aprendizagem dos alunos.
5 REFERÊNCIAS
BARRETO, A. O ensino de cálculo I nas universidades. Informativo da Sociedade
Brasileira de Matemática – SBM, 1995.
BARROS, Rodolfo M.; MELONI, Luís G. P. O processo de ensino e aprendizagem de
Cálculo Diferencial e Integral por meio de metáforas e recursos multimídia. Anais do
XXXIV Congresso Brasileiro de Ensino de Engenharia. Passo Fundo, Setembro, 2006.t
BOYER, Carl B. História da Matemática. 2 ed. São Paulo. Edgard Blücher Ltda, 1996
COXE, Infeliz C. Ensino e aprendizagem de integrais de funções racionais usando
software Maple.VII CIBEM, Montevideo, Uruguai. 16 a 20 de setembro de 2013.
BRASIL, Ministério da Educação e Cultura. Diretrizes Curriculares para Cursos de
Graduação. 2002.
BRASIL, Ministério da Educação e Cultura. Instituições de Educação Superior e Cursos
Cadastrados. Disponível em < http://emec.mec.gov.br/> Acesso em 25 de janeiro de 2014.
BRASIL, Ministério da Educação e Cultura. Biblioteca Básica para os cursos de
Administração
do
País.
Disponível
em
<http://portal.mec.gov.br/sesu/arquivos/pdf/ad_bibl.pdf>. 2004. Acesso em 23 de janeiro de
2014.
D’AMBRÓSIO, U. A matemática nas escolas. Educação matemática em revista. Ano 9, nº
11, edição especial, p. 29-33, abril de 2002 .
FRESCKI, Franciele B.; PIGATTO, Priscila. Dificuldades na aprendizagem de Cálculo
Diferencial e Integral na educação tecnológica: proposta de um curso de nivelamento.
Universidade Tecnológica Federal do Paraná Anais do I Simpósio Nacional de Ensino de
Ciência e tecnologia, Curitiba: UTFPR, 2009.
IRIAS, Diánis, F. et al. Cálculo Diferencial e Integral I: analisando as dificuldades dos
alunos de um curso de Licenciatura em Matemática. Revista de Educação Matemática,
UFOP. Vol. I, 2011 – XI Semana de Matemática e III Semana de Estatística,2011.
JESUS, Cristiano S., et al. Reflexões sobre o ensino de Cálculo Diferencial e Integral I:
UFOP e IFMG-OP numa parceria pela busca da diminuição do índice de reprovação na
disciplina. X Semana da Matemática e II Semana da Estatística, 2010. Revista de Educação
Matemática da UFOP, Vol I, 2011.
LACAZ, Tania M.V.S. et al. Implicações das dificuldades dos alunos na aprendizagem da
disciplina Cálculo Diferencial e Integral I da FEG/UNESP para as práticas pedagógicas.
XXXV Congresso Brasileiro de Educação em Engenharia.2007.
MELLO, João C.C.B.S et al. Mudanças no Ensino de Cálculo I: Histórico e Perspectivas.
Congresso Brasileiro de Educação em Engenharia. 2001.
NASCIMENTO, Jorge L. Uma proposta metodológica para a disciplina de Cálculo I. VI
Encontro de Educação em Engenharia. Universidade Federal do Rio de Janeiro.27 de
novembro a 01 de dezembro de 2000.
RAAD, Marcos R. História do ensino de Cálculo Diferencial: a existência de uma cultura.
Dissertação de Mestrado. Instituto de Ciências Exatas. Programa de Pós Graduação em
Educação Matemática. Mestrado Profissional em Educação Matemática. Juiz de Fora, Minas
Gerais, 2012.
SANTOS, Sílvia P.; MATOS, Márcia G.O. O ensino de Cálculo I no curso de Licenciatura
em Matemática: obstáculos na aprendizagem. Revista Eventos Pedagógicos, v.3, n.3, p.458473, Agosto – Dezembro, 2012.
SANTOS, Marcéu V.R. CARNEIRO, Isabel M.D.P. Dificuldades de aprendizagem no
ensino de Cálculo Diferencial e Integral: implicações para o trabalho docente. XXI
Encontro de Pesquisa Educacional do Norte e Nordeste. Universidade Federal de
Pernambuco. 10 a 13 de novembro de 2013.
SILVA, Michele A. ; et.al. Dificuldades de aprendizagem na disciplina de cálculo
diferencial e integral: estudo de caso com alunos do curso de licenciatura em química. In:
congresso de pesquisa e inovação da rede norte e nordeste de educação tecnológica- v
CONNEPI, 2010, Alagoas. Congresso De Pesquisa e Inovação Da Rede Norte E Nordeste De
Educação Tecnológica- V CONNEPI, 2010.
SOUZA, Veriano C. A origem do Cálculo Diferencial e Integral. Monografia. Universidade
Candido Mendes Rio de Janeiro, 2001.
SWOKOWSKI, Earl W. Cálculo com Geometria Analítica
Editora Makron Books, 1994.
. 2º edição. São Paulo.
WROBEL, Julia S. et. al. O mapa do ensino de Cálculo nos últimos 10 anos do
COBENGE. XLI Congresso Brasileiro de Educação em Engenharia. Gramado, Rio Grande
do Sul. 2013.
THE TEACHING OF DIFFERENTIAL AND INTEGRAL CALCULUS
IN A COURSE OF BUSINESS ADMINISTRATION: MAIN
DIFFICULTIES LEARNING STUDENTS
Abstract: The teaching of Differential and Integral Calculus is linked to various
undergraduate courses, especially those connected to the area of Exact and Engineering. Yet
few courses in the area of Applied Social are also used concepts of this discipline in their
program. This is the case of the Administration course that uses concepts of Calculus in order
to develop in its students the ability to mathematical reasoning and logic to be applied in
various situations. The purpose of this article is to examine the major learning difficulties of
students in a course of Directors in related Calculation discipline from a University of
Paraná state. The students were subjected to a questionnaire default, so try to understand if
there were real difficulties and investigate the main factors that limit the learning of the
discipline. The students were subjected to a questionnaire with pre-defined questions and the
results were summarized in graphs. It was realized the real difficulty of the students in
learning the discipline, and the need that students see themselves in a preliminary discipline
that will help them with basic math content.
Keywords: Teaching, Learning, Differential and Integral Calculus, Course Directors
Administration.