Din Mov Circular

DINÂMICA DO MOVIMENTO CIRCULAR
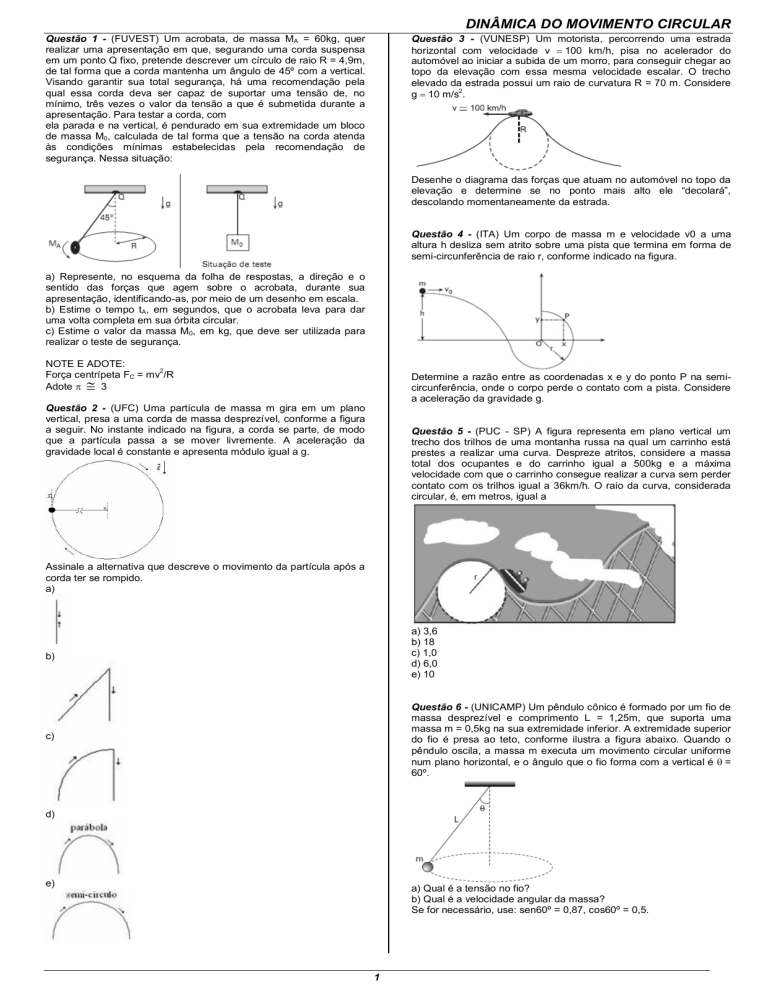
Questão 1 - (FUVEST) Um acrobata, de massa MA = 60kg, quer
realizar uma apresentação em que, segurando uma corda suspensa
em um ponto Q fixo, pretende descrever um círculo de raio R = 4,9m,
de tal forma que a corda mantenha um ângulo de 45º com a vertical.
Visando garantir sua total segurança, há uma recomendação pela
qual essa corda deva ser capaz de suportar uma tensão de, no
mínimo, três vezes o valor da tensão a que é submetida durante a
apresentação. Para testar a corda, com
ela parada e na vertical, é pendurado em sua extremidade um bloco
de massa M0, calculada de tal forma que a tensão na corda atenda
às condições mínimas estabelecidas pela recomendação de
segurança. Nessa situação:
Questão 3 - (VUNESP) Um motorista, percorrendo uma estrada
horizontal com velocidade v 100 km/h, pisa no acelerador do
automóvel ao iniciar a subida de um morro, para conseguir chegar ao
topo da elevação com essa mesma velocidade escalar. O trecho
elevado da estrada possui um raio de curvatura R = 70 m. Considere
g 10 m/s2.
Desenhe o diagrama das forças que atuam no automóvel no topo da
elevação e determine se no ponto mais alto ele “decolará”,
descolando momentaneamente da estrada.
Questão 4 - (ITA) Um corpo de massa m e velocidade v0 a uma
altura h desliza sem atrito sobre uma pista que termina em forma de
semi-circunferência de raio r, conforme indicado na figura.
a) Represente, no esquema da folha de respostas, a direção e o
sentido das forças que agem sobre o acrobata, durante sua
apresentação, identificando-as, por meio de um desenho em escala.
b) Estime o tempo tA, em segundos, que o acrobata leva para dar
uma volta completa em sua órbita circular.
c) Estime o valor da massa M0, em kg, que deve ser utilizada para
realizar o teste de segurança.
NOTE E ADOTE:
Força centrípeta FC = mv2/R
Adote   3
Determine a razão entre as coordenadas x e y do ponto P na semicircunferência, onde o corpo perde o contato com a pista. Considere
a aceleração da gravidade g.
Questão 2 - (UFC) Uma partícula de massa m gira em um plano
vertical, presa a uma corda de massa desprezível, conforme a figura
a seguir. No instante indicado na figura, a corda se parte, de modo
que a partícula passa a se mover livremente. A aceleração da
gravidade local é constante e apresenta módulo igual a g.
Questão 5 - (PUC - SP) A figura representa em plano vertical um
trecho dos trilhos de uma montanha russa na qual um carrinho está
prestes a realizar uma curva. Despreze atritos, considere a massa
total dos ocupantes e do carrinho igual a 500kg e a máxima
velocidade com que o carrinho consegue realizar a curva sem perder
contato com os trilhos igual a 36km/h. O raio da curva, considerada
circular, é, em metros, igual a
Assinale a alternativa que descreve o movimento da partícula após a
corda ter se rompido.
a)
b)
a) 3,6
b) 18
c) 1,0
d) 6,0
e) 10
c)
Questão 6 - (UNICAMP) Um pêndulo cônico é formado por um fio de
massa desprezível e comprimento L = 1,25m, que suporta uma
massa m = 0,5kg na sua extremidade inferior. A extremidade superior
do fio é presa ao teto, conforme ilustra a figura abaixo. Quando o
pêndulo oscila, a massa m executa um movimento circular uniforme
num plano horizontal, e o ângulo que o fio forma com a vertical é =
60º.
d)
e)
a) Qual é a tensão no fio?
b) Qual é a velocidade angular da massa?
Se for necessário, use: sen60º = 0,87, cos60º = 0,5.
1
DINÂMICA DO MOVIMENTO CIRCULAR
Questão 7 - (VUNESP) Suponha que um predador de massa 150kg
possa atingir e manter uma velocidade de 40m/s, enquanto persegue
uma presa de massa 60kg que, por sua vez, corre a 30m/s.
a) Se ambos estiverem correndo no mesmo sentido, numa mesma
reta, e num dado instante a presa ficar 60 metros à frente, quanto
tempo mais demoraria para ela ser pega?
b) Uma estratégia para fugir é fazer uma curva. Calcular quais devem
ser as forças necessárias para presa e predador fazerem uma curva
circular de raio 5,0m, mantendo, em módulo, os valores das
velocidades indicadas acima.
atrito, não poderá estar animado com qualquer velocidade; existe um
valor máximo. Sendo g, o módulo do vetor aceleração gravitacional
local, m a massa do automóvel e estando ele com a velocidade
máxima,
Questão 8 - (VUNESP) Um garoto amarra uma pedra de 250g na
ponta de um barbante de 1,0m de comprimento e massa desprezível.
Segurando na outra extremidade do barbante, ele gira o sistema
fazendo a pedra descrever círculos verticais com velocidade escalar
constante igual a 6,0m/s em torno do ponto em que o barbante é
seguro. Adotando g = 10m/s2, as trações no fio no ponto mais alto
(Ta) e no ponto mais baixo (Tb) da trajetória valem:
a) Ta = Tb = 9,0N.
b) Ta = 2,0N; Tb = 5,0N.
c) Ta = 5,0N; Tb = 2,0N.
d) Ta = 6,5N; Tb = 11,5N.
e) Ta = 11,5N; Tb = 6,5N.
sua Energia Cinética é
m.R.g.sen
2
a) Ec =
m.R.g
b) Ec = 2 sen
m.R.g.tg
2
c) Ec =
m.R.g.
2.tg 
d) Ec =
m.R.g. cos 
4
e) Ec =
Questão 9 - (VUNESP) Depois de anos de interrupção, ocorreu
neste ano a retomada de lançamentos do ônibus espacial pela
NASA, desta vez com sucesso. Nas imagens divulgadas do dia-a-dia
no ônibus espacial girando ao redor da Terra, pudemos ver os
astronautas realizando suas atividades, tanto fora da nave como no
seu interior. Considerando que as órbitas da nave e dos astronautas
sejam circulares, analise as afirmações seguintes.
I.
Não há trabalho realizado pela força gravitacional para
manter um astronauta em órbita ao redor da Terra.
II.
A aceleração de um astronauta girando ao redor da Terra
deve-se exclusivamente à ação da força gravitacional.
III.
A velocidade vetorial do astronauta ao redor da Terra é
constante.
Estão corretas as afirmações:
a) II, somente.
b) III, somente.
c) I e II, somente.
d) II e III, somente.
e) I, II e III.
Questão 12 - (Vunesp) Em um modelo atômico simples, proposto por
Bohr em 1913, um núcleo contendo prótons e nêutrons é rodeado por
elétrons que giram em órbitas circulares de raio rn, onde a força de
atração elétrica do núcleo positivo sobre cada elétron segue a lei de
Coulomb. Utilizando esse modelo para o caso do átomo de
hidrogênio (um único elétron girando em torno de um núcleo que
contém um próton),
a) determine a direção, o sentido e a expressão para o módulo da
força elétrica, atuando sobre o elétron, em função da carga e do
elétron, do raio rn e da constante eletrostática no vácuo K.
b) determine a expressão para a velocidade v da órbita do elétron em
função da carga e e da massa me do elétron, do raio rn e da
constante eletrostática no vácuo K.
Questão 10 - (UECE) Quando o átomo de hidrogênio emite um fóton,
o elétron passa de uma órbita de raio
r2 , para uma órbita de raio
r1  r2 , variando assim sua velocidade orbital de v 2 para v1 .
Sendo m e e a massa e a carga do elétron, respectivamente, e k
Questão 13 - (UFC) Uma partícula P, de massa m, descreve um
movimento circular de raio R, centrado no ponto O, sob a ação das
a constante eletrostática, a variação no módulo da velocidade do
elétron da órbita maior para a órbita menor é:
 ke2 

v 2  v1  
 m 
1
 ke2 

v 2  v1  
 m 
1
2
a)
b)
2
F
1
 1  12
 1  2
     
r  
 r2 
 1 

1
 1  12
 1  2
     
r  
 r1 
 2 

1
c)
ke2  r1  r2 


v 2  v1 
m  r1r2 
d)
 ke2  r1  r2 


v 2  v1  
 m  r1r2 
F
1 e
2 , conforme figura ao lado. Das equações de
forças
movimento apresentadas nas alternativas abaixo, assinale a correta
para este sistema.
Considere:
at a aceleração tangencial da partícula P
vp a velocidade tangencial da partícula P
2
1
2
a) F2 cos  = ma t
b) F1 + F2 = m
 V p2

 R





 V p2

 R
c)F1 - F2 cos  = m 
Questão 11 - (Mack) Objetivando melhorar a segurança dos
automóveis
nos
trechos
não
retilíneos
das
estradas,
independentemente do atrito entre suas rodas e o plano da pista,
utiliza-se o recurso da sobrelevação da parte “externa” da pista na
curva. Desta forma, tem-se uma inclinação do plano da pista em
relação à horizontal. Para um automóvel descrever uma trajetória
circunferencial de raio R, sem derrapar e independentemente do
2




DINÂMICA DO MOVIMENTO CIRCULAR
V

 R

2
p
d) F1 - F2 = m
e) F1 = m
 V p2

 R









Se o coeficiente de atrito estático com o solo é µ = 0,80, assinale a
opção correta que indica, respectivamente, a velocidade do ciclista,
o tempo despendido no percurso e a freqüência de ziguezague no
trecho BE.
a) 6,0m/s 6,0s
0,17s-1
b) 4,0m/s 12s
0,32s-1
c) 9,4m/s 3,0s
0,22s-1
d) 6,0m/s 3,1s
0,17s-1
-1
e) 4,0m/s 12s
6,0 s
Questão 14 - (FMTM) Segurando as mãos de seu filho com as suas,
uma mãe põe se a girá-lo uniformemente a uma razão de meia volta
por segundo, fazendo com que o menino fique temporariamente
suspenso no ar. Se durante a rotação a criança de 15 kg tem seu
centro de massa mantido a 1 m do corpo da mãe, a força centrípeta
que o centro de massa da criança experimenta, em N, é
Adote: = 3
a) 45.
b) 60.
c) 95.
d) 110.
e) 135.
Questão 18 - (Fuvest) Um brinquedo consiste em duas pequenas
bolas A e B, de mesma massa M, e um fio flexível: a bola B está
presa na extremidade do fio e a bola A possui um orifício pelo qual o
fio passa livremente. Para o jogo, um operador (com treino!) deve
segurar o fio e girá-lo, de tal forma que as bolas descrevam
trajetórias circulares, com o mesmo período T e raios diferentes.
Questão 15 - (UFV) A figura abaixo ilustra uma esfera de massa m =
1,9 kg, lançada do ponto A com uma velocidade de módulo 20 m/s.
Presa a um fio inextensível, de massa desprezível e de comprimento
L = 3,8 m, ela passa a mover-se em um plano vertical descrevendo
uma trajetória circular.
Nessa situação, como indicado na figura 1, as bolas permanecem em
lados opostos em relação ao eixo vertical fixo que passa pelo ponto
O. A figura 2 representa o plano que contém as bolas e que gira em
torno do eixo vertical, indicando os raios e os ângulos que o fio faz
com a horizontal.
Assim, determine:
a) O módulo da força de tensão F, que permanece constante ao
longo de todo o fio, em função de M e g.
b) A razão K = sen / senθ, entre os senos dos ângulos que o fio faz
com a horizontal.
c) O número N de voltas por segundo que o conjunto realiza quando
o raio R1 da trajetória descrita pela bolinha B for igual a 0,10m.
Sabe-se que o fio suporta uma tensão máxima de 500 N e que a
aceleração gravitacional local é 10,0 m/s2. Desprezando quaisquer
efeitos dissipativos, faça o que se pede:
a) determine os módulos das velocidades da esfera nos pontos B e
C.
b) determine o módulo da tensão no fio no ponto B.
c) verifique se a esfera vai atingir o ponto D, ou seja, se o fio não se
romperá antes. Justifique sua resposta.
Questão 16 - (ITA) Um objeto pontual de massa m desliza com

NOTE E ADOTE:
Não há atrito entre as bolas e o fio.
Considere senθ = 0,4 e cosθ = 0,9;  = 3
velocidade inicial v , horizontal, do topo de uma esfera em repouso,
de raio R. Ao escorregar pela superfície, o objeto sofre uma força de
atrito de módulo constante dado por f = 7mg/4.
Questão 19 - (PUC-RJ) Um pêndulo simples de massa m = 1,0 kg e
comprimento C = 10 cm é deslocado de um ângulo
em relação à
vertical e largado. Sabendo-se que o pêndulo tem velocidade de 1,0
m/s imediatamente antes de colidir elasticamente com um bloco de
igual massa inicialmente em repouso, como mostra a figura, calcule:
Para que o objeto se desprenda da superfície esférica após percorrer
um arco de 60° (veja figura), sua velocidade inicial deve ter o módulo
de:
a)
b)
c)
d)
e)
a) o ângulo ;
b) a tração na corda imediatamente antes da colisão;
c) o momento linear do bloco imediatamente após a colisão;
d) Se, imediatamente após a colisão, o bloco se desloca num terreno
acidentado, sendo o coeficiente de atrito cinético entre o bloco e o
terreno igual a 0,2, qual é a distância percorrida pelo bloco até parar?
(Considere a massa e o bloco como sendo pontuais, e g = 10 m/s2 ).
2gR / 3
3gR / 2
6gR / 2
Questão 20 - (AFA) A figura abaixo representa uma pista
pertencente ao plano vertical. O raio R da parte circular vale 4 m. Um
corpo parte do repouso no ponto A. Desprezando o atrito e a
resistência do ar e considerando que, em B, a força que comprime o
móvel contra a pista vale 1/4 do seu peso, pode-se afirmar que, a sua
velocidade em B vale, em m/s, aproximadamente,
3 gR / 2
3 gR
Questão 17 - (ITA) A figura representa o percurso de um ciclista,
num plano horizontal, composto de dois trechos retilíneos (AB e EF),
cada um com 6,0m de comprimento, e de um trecho sinuoso
intermediário formado por arcos de circunferências de mesmo
diâmetro, igual a 4,0m, cujos centros se encontram numerados de 1
a 7. Considere pontual o sistema ciclista-bicicleta e que o percurso é
completado no menor tempo, com velocidade escalar constante.
a) 3,2.
b) 5,5.
c) 6,3.
d) 7,1.
3
DINÂMICA DO MOVIMENTO CIRCULAR
Questão 21 - (UFBA) Na figura abaixo, um pêndulo simples, de
massa m e comprimento l, é abandonado, a partir do repouso, no
ponto A. Considere o módulo da aceleração da gravidade local igual
a g e despreze a ação de forças dissipativas.
a) 2o
b) 7o
c) 13o
d) 17o
e) 20o
Questão 24 - (UFSCar) A figura a seguir representa um pêndulo
cônico, composto por uma pequena esfera de massa 0,10kg que gira
presa por um fio muito leve e inextensível, descrevendo círculos de
0,12m de raio num plano horizontal, localizado a 0,40m do ponto de
suspensão. (Adote g = 10m/s2.)
Com base nessas informações e na análise da figura:
a) Faça um esboço do diagrama vetorial das forças que agem na
massa pendular, identificando cada uma delas, quando a massa
passa pelo ponto B da trajetória.
b) Determine, em função de g, o módulo da aceleração centrípeta da
massa pendular, quando ela passa pelo ponto C da trajetória.
c) Determine, em relação ao plano de referência e em função de m, l,
g e , a energia potencial gravitacional da massa pendular no ponto
D da trajetória.
Questão 22 - (Fuvest) Um astrônomo, ao estudar uma estrela dupla
E1-E2 , observou que ambas executavam um movimento em torno de
um mesmo ponto P, como se estivessem ligadas por uma barra
imaginária. Ele mediu a distância D entre elas e o período T de
rotação das estrelas, obtendo T = 12 dias. Observou, ainda, que o
raio R1 , da trajetória circular de E1 , era três vezes menor do que o
raio R2 , da trajetória circular de E2 . Observando essas trajetórias,
ele concluiu que as massas das estrelas eram tais que M1 = 3 M2 .
Além disso, supôs que E1 e E2 estivessem sujeitas apenas à força
gravitacional entre elas. A partir das medidas e das considerações do
astrônomo:
a) Represente graficamente, na folha de respostas, as forças que
atuam sobre a esfera, nomeando-as. Determine o módulo da
resultante dessas forças.
b) Determine o módulo da velocidade linear da esfera e a freqüência
do movimento circular por ela descrito.
Questão 25 - (SpeedSoft) O pêndulo da figura oscila em condições
ideais, invertendo seu movimento sucessivamente nos pontos A e C.
A esfera tem massa de 1,0 kg e o comprimento do fio leve e
inextensível vale 2,0 m. Sabendo-se que no ponto B (mais baixo da
trajetória) a esfera tem velocidade de módulo 2,0 m/s e que g = 10
m/s² , pede-se determinar:
a) Indique as posições em que E1 e E2 estariam, quinze dias após
uma observação em que as estrelas foram vistas, como está
representado no esquema da folha de respostas. Marque e
identifique claramente as novas posições de E1 e E2 no esquema da
folha de respostas.
b) Determine a razão R = V2/V1 entre os módulos das velocidades
lineares das estrelas E2 e E1 .
c) Escreva a expressão da massa M1 da estrela E1 , em função de T,
D e da constante universal da gravitação G.
a) a intensidade da força que traciona o fio, quando a esfera passa
pelo ponto B.
b) a intensidade da força que tracionaria o fio, se a esfera estivesse
em repouso no ponto B.
Questão 26 - (SpeedSoft) Um carrinho de brinquedo, cuja massa
vale 4,0 kg, descreve movimento circular e uniforme sobre uma mesa
horizontal sem atrito, com velocidade de 18 km/h. Um fio ideal, de
comprimento 1,0 m, prende-o ao centro de rotação, conforme ilustra
o esquema abaixo.
a) O carrinho é dotado de aceleração ? Explique.
b) Calcule a tração no fio.
c) Se o fio suportar uma tração máxima de 256 N, qual a máxima
velocidade que o carrinho poderá se mover sem que o fio arrebente ?
Questão 23 - (Mack) Um veículo necessita deslocar-se num trecho
circunferencial de um autódromo, com velocidade escalar constante
de 180 km/h. O raio de curvatura da trajetória é 820 m. Para que
esse movimento seja possível, independentemente do atrito entre os
pneus e a pista, a estrada deverá apresentar uma sobrelevação, em
relação à horizontal, correspondente a um ângulo a mínimo,
aproximadamente igual a:
2o
7o
13o
17o
20o
sen
0,035
0,122
0,225
0,292
0,342
cos
0,999
0,992
0,974
0,956
0,940
tan
0,035
0,123
0,231
0,306
0,364
Questão 27 - (Unicamp) As máquinas a vapor, que foram
importantíssimas na Revolução Industrial, costumavam ter um
engenhoso regulador da sua velocidade de rotação, como é
mostrado esquematicamente na figura abaixo. As duas massas
afastavam-se do eixo devido ao movimento angular e acionavam um
dispositivo regulador da entrada de vapor, controlando assim a
velocidade de rotação, sempre que o ângulo  atingia 30°. Considere
hastes de massa desprezível e comprimento L = 0,2 m, com massas
m = 0,18 kg em suas pontas, d = 0,1 m e aproxime
4
3
 1,8.
DINÂMICA DO MOVIMENTO CIRCULAR

d
articulação
L

m
m
a) Faça um diagrama indicando as forças que atuam sobre uma das
massas m.
b) Calcule a velocidade angular  para a qual  = 30o .
Como a trajetória é uma circunferência, e considerando que se trata
de movimento uniforme, a resultante no acrobata é centrípeta, isto é,
de acordo com a figura anterior, horizontal e para a direita. Assim
sendo, podemos estabelecer relação entre as forças e a resultante
por meio do método da linha poligonal.
Questão 28 - (Fuvest) Um carrinho é largado do alto de uma
montanha russa, conforme a figura. Ele se movimenta, sem atrito e
sem soltar-se dos trilhos, até atingir o plano horizontal. Sabe-se que
os raios de curvatura da pista em A e B são iguais. Considere as
seguintes afirmações:
I.
No ponto A, a resultante das forças que agem sobre o
carrinho é dirigida para baixo.
II.
A intensidade da força centrípeta que age sobre o carrinho
é maior em A do que em B.
III.
No ponto B, o peso do carrinho é maior do que a
intensidade da força normal que o trilho exerce sobre ele.
Utilizando a trigonometria:
T apres. = 600
2
N
Como a intensidade do Peso é 600N, a figura pedida pode ser assim
representada.
a)
Está correto apenas o que se afirma em
a) I
b) II
c) III
d) I e II
e) II e III
Questão 29 - (Unicamp) Uma atração muito popular nos circos é o
"Globo da Morte" , que consiste numa gaiola de forma esférica no
interior da qual se movimenta uma pessoa pilotando uma
motocicleta. Considere um globo de raio R = 3,6 m.
b) A partir do triângulo da figura 1:
Rc = P
Utilizando o princípio fundamental da dinâmica aplicado para o MCU,
dado no quadro NOTE E ADOTE, e a expressão para o cálculo da
intensidade do Peso
V2
R
a) Faça um diagrama das forças que atuam sobre a motocicleta nos
pontos A, B, C e D indicados na figura abaixo, sem incluir as forças
de atrito. Para efeitos práticos, considere o conjunto piloto +
motocicleta como sendo um ponto material.
b) Qual a velocidade mínima que a motocicleta deve ter no ponto C
para não perder o contato com o interior do globo?
= g (1)
Aplicando a definição de velocidade escalar média para uma volta do
movimento do acrobata:
v=
2R
T
(2)
Substituindo (2) em (1): T = 4,2s
Questão 30 - (UFRJ) Uma pequena esfera metálica, suspensa por
um fio ideal de comprimento l a um suporte, está oscilando num
plano vertical, com atritos desprezíveis, entre as posições extremas,
A e B, localizadas a uma altura h = l / 2 acima do ponto mais baixo C
de sua trajetória, como ilustra a figura:
c) De acordo com o enunciado, a corda deve ser capaz de suportar
uma tensão de, no mínimo, três vezes o valor da tensão a que é
submetida durante a apresentação. Considerando que não haja
variação nas dimensões da corda, podemos afirmar que a tração
apresenta o mesmo comportamento.
Tfio suporta  3 . Tapres.
 Tfio suporta  3.600 2
Tfio suporta 1800 2 N (3)
A figura abaixo representa as forças aplicadas no bloco de massa M0
na situação de teste:
Considere g = 10m/s2.
a) Calcule o módulo de aceleração da esfera dos instantes em que
ela passa pelos pontos A e B.
b) Calcule o módulo da aceleração da esfera nos instantes em que
ela passa pelo ponto C.
GABARITO
Questão 1 - A figura a seguir, que está fora de escala, representa,
em um plano vertical, a situação descrita no enunciado e as forças
aplicadas no acrobata.
Como na situação de teste o corpo está em repouso
Tteste = P ⇒ Tteste = M0 ⋅ g (4)
A situação de teste é feita para que seja obtida a tração que o fio
deve suportar, assim sendo,
5
DINÂMICA DO MOVIMENTO CIRCULAR
podemos substituir (4) em (3).
MO . g  1200
MO  180
2
Questão 22 - a)
2
kg
Questão 2 - Alternativa: A
Questão 3 - V = 95,2 km/h
Como a velocidade do automóvel é maior do que a mínima calculada,
ele "decolará", descolando- se da estrada.
Questão 4 - Resposta:
x
y
=
9 g 2 r 2  (v02  2 gh) 2
M1 
v02  2 gh
b) R = 3
c)
3 2 D 3
GT 2
Questão 23 - Alternativa: D
Questão 5 - Alternativa: E
Questão 24 - a) R = 0,30 N
Questão 6 - Respostas:
a) T10N
b)  = 4rad/s
Consideramos que o examinador queria saber o valor da tração no
fio no item a, já que seria impossível calcular o valor da tensão no
mesmo, dado que não é conhecida a área de sua seção transversal.
Questão 7 - a) Levaria 6s para que o predador alcançasse a presa.
b) v = 0,6 m/s e f = 0,8 Hz
40 2
b) Predador: Rc(1) = 150. 5 =48000 N
30 2
Presa: Rc(2) = 60. 5 = 10800N
Questão 25 - a) T = 12N
b) T = 10N
Questão 26 - a) sim, possui acentrípeta, pois realiza uma curva, e a
direção de sua velocidade varia.
b) T = 100 N
c) v = 8 m/s = 28,8 km/h
Questão 27 - a) Colocando as forças em apenas um dos corpos:
Questão 8 - Alternativa: D
Questão 9 - Alternativa: C
Questão 10 - Alternativa: C
Questão 11 - Alternativa: C
Questão 12 - a) • A direção de Fé a da reta que passa pelo próton
e pelo elétron.
• O sentido é do elétron para o próton (atração).
v e
b)
k
me .rn
Questão 13 - Alternativa: C
b)
Questão 14 - Alternativa: E
Questão 15 - a) vB = 18 m/s e vC = 20 m/s
b) TB = 143 N
c) TD = 471,2 N < 500 N e portanto o fio não romperá.
Questão 16 - Alternativa: A
Questão 17 - Alternativa: B
Questão 18 - a) F = 2,5 Mg
b) k = 2
Questão 19 - a)  = 60o
  30m / s  5,47rad / s
Questão 28 - Alternativa: E
Questão 29 - a) As forças que atuam na motocicleta estão
representadas na figura abaixo:
c) N = 2,5 Hz
b) T = 20 N c) Q = 1 kgm/s d) d = 0,25 m
Questão 20 - Alternativa: D (considerando g =10 m/s2 e o ponto B o
mais alto da trajetória)
Questão 21 - a)
b) V = 6 m/s
Questão 30 - a) aA = aB = g = 10 m/s2 (para baixo)
b) aC = 10 m/s2 (para cima)
b) ac = 2g
c) Ep = m

g l

(1-cos)
6