MAT01102 - Cálculo IB - Charles? Que Charles?

MAT 01102 - Cálculo I-B
http://localhost/UFRGS/MAT 01102.html
MAT01102 - Cálculo I-B
Aula do dia 23/05/2011
Limites envolvendo o infinito
limx
f(x) = + , se f(x) fica arbitrariamente grande, quando x está
suficientemente próxima de a.
a
(análogo para −
)
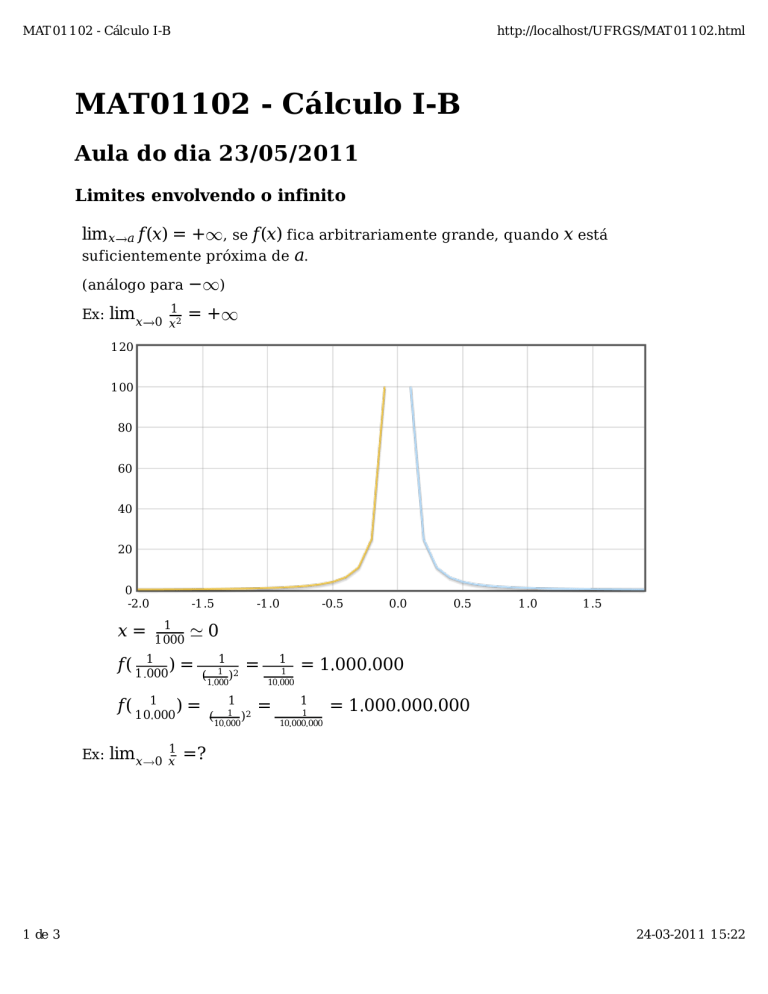
Ex: lim x 0 12 = +
x
120
100
80
60
40
20
0
-2.0
x=
-1.5
1
1000
f( 1 1000) =
-1.0
-0.5
0.0
0.5
1.0
1.5
0
1
1 2
(1 000
)
f( 101000) =
=
1
1
(10 000
)2
1
1
10 000
=
= 1 000 000
1
1
10 000 000
= 1 000 000 000
Ex: lim x 0 x1 =?
1 de 3
24-03-2011 15:22
MAT 01102 - Cálculo I-B
http://localhost/UFRGS/MAT 01102.html
15
10
5
0
-5
-10
-15
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
Não existe, pois
limx
limx
1
0+ x
=+
limx
1
0− x
=−
+
f(x) = a, se f(x)
(análogo para −
1
x2
=0
Ex: lim x −
1
x2
=0
Ex: lim x +
1
x 2+1
=0
Ex: lim x +
6x−1
2x+1
=?
+
6x−1
2x+1
= limx
1
x
Como lim x +
limx
+
Ex: lim x −
limx
−
Ex: lim x +
2 de 3
6−0
2+0
+
x(6−1x)
x(2+1x)
= 0 temos que:
=3
3x 2+1
2x+1
=?
3x 2+1
2x+1
3x+1
2x 2
+ .
)
Ex: lim x +
limx
a quando x
= limx
−
x(3x+1x)
x(2+1x)
= limx
−
3x+0
2+0
= limx
−
3x
2
=−
=?
24-03-2011 15:22
MAT 01102 - Cálculo I-B
limx
+
http://localhost/UFRGS/MAT 01102.html
3x+1
2x 2
Como lim x +
limx
+
3x+1
2x 2
= limx
3+
1
x
x(3+1x)
x(2x)
−
= limx
= 3 e limx
+
3+1x
2x
−
2x = +
temos que:
=0
Teorema sobre limites
Suponha existir lim x a f(x) lim x a g(x).
Então:
1. lim x a (cte)f(x) = (cte) lim x a f (x)
v
2. Se v
0, então limx a (f(x))v = limx a f (x)
3. lim x a (f(x) + g(x)) = lim x a f (x) + lim x a g(x)
4. lim x a (f(x) g(x)) = (lim x a f (x)) (lim x a g(x))
h(x)=f (x)
; f,g são funções polinomiais;
g(x)
(x)
(a)
limx a fg(x)
= fg(a)
5. Se
a
e g(a) = 0
2
2(2)2+3x2−1
Ex: lim x 2 2x +3x−1
=
= 13
7
2x 2−1
2(2)2−1
2
(x−2)(x+2)
x+2
2+2
Ex: lim x 2 2x −4 = lim x 2
= limx 2 x+1
= 2+1
= 43
(x−2)(x+1)
x −x−2
Ex:
limx
+
3x 4+2x−1
2x 3+7x
= limx
+
x 3(3x+ 22)
x
x 3(5+3x− 12)
= limx
x
+
3x+0−0
2+0
= limx
+
3x = +
Ex:
limx
3 de 3
−
2x 4+1
x 2−2x
= limx
Ex: lim x −
x 2+1
x 4−1
Ex: lim x −
−2x 5+4x
3x+1
−
= limx
x 2(2x 2+ 12)
x
x 2(1−2x)
−
= limx
= limx
x 2(1+ 12)
x
2
2
x (x − 12)
x
−
−2x 4
3
= limx
2x 2+0
1−0
−
−
1+0
x 2−0
= limx
=
limx
2x2 = +
−
+
x2
1
=0
=−
24-03-2011 15:22