Resolução dos Exercícios de Eletrônica Básica Os materiais

Resolução dos Exercícios de Eletrônica Básica
1. Os materiais elétricos, classificados por resistividade, do maior para o menor, são:
condutores, semicondutores e isolantes.
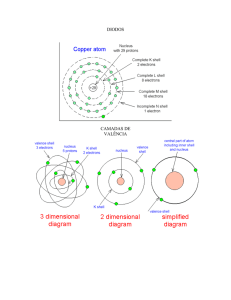
2. O boro é um elemento trivalente, que quando forma uma ligação com o silício
(tetravalente), acaba ficando com uma ligação a menos. Esses “buracos” facilitam a
circulação dos elétrons, que se desprendem de ligações covalentes para preenchê-los
quando há excitação ou aplicação de tensão sobre o material. Dessa maneira, os
portadores majoritários são os buracos e o material é caracterizado como do tipo p,
pois possui portadores majoritários de carga positiva.
3. O fósforo é um elemento pentavalente, que ao formar uma ligação com o silício,
sobram elétrons livres em sua eletrosfera. Estes elétrons são portadores majoritários,
e, portanto, o material é do tipo n.
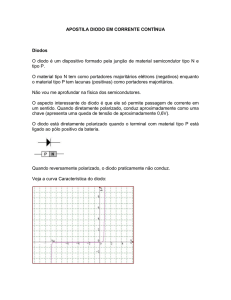
4. A polarização direta ocorre quando o anodo (feito de material tipo p) é submetido a
um potencial maior que o catodo (material tipo n), fazendo com que a região de
depleção diminua de intensidade e o diodo conduza corrente. A polarização reversa
ocorre quando o catodo é submetido a um potencial menor que o do anodo, fazendo
com que a região de depleção se intensifique e impedindo a circulação de corrente no
diodo.
5. Ver (4) acima.
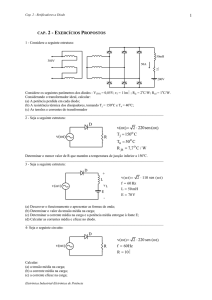
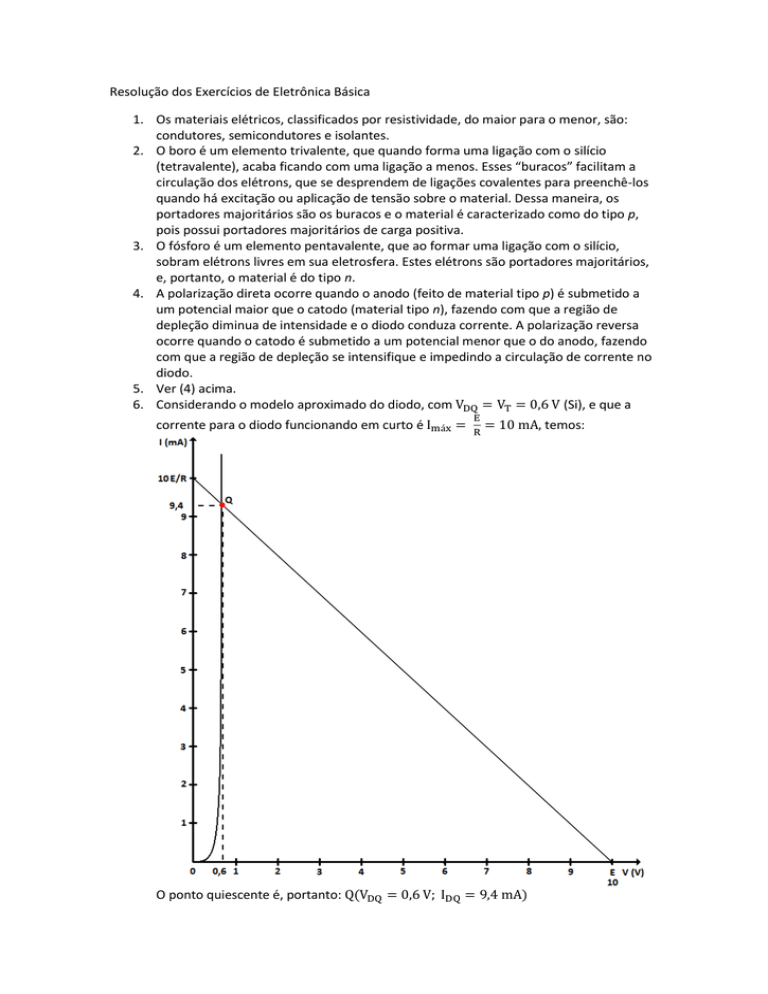
6. Considerando o modelo aproximado do diodo, com VDQ = VT = 0,6 V (Si), e que a
corrente para o diodo funcionando em curto é Imáx =
E
R
= 10 mA, temos:
O ponto quiescente é, portanto: Q(VDQ = 0,6 V; IDQ = 9,4 mA)
7. Utilizando o modelo simples do diodo, temos:
VDQ = VT = 0,5 V
VR = E − VDQ = 9,5 V
VR
9,5
IDQ = IR =
=
= 9,5 mA
R
1000
8. A tensão média Vm do resistor para a situação de meia onda é dado pela fórmula:
V
Vm = máx
π
Onde Vmáx é o valor máximo da tensão fornecida pela fonte de tensão alternada E ao
resistor, menos a queda de tensão do diodo.
Temos:
E
−V 9,3
Vm = máxπ T π = 2,96 V
9. A tensão média Vm do resistor para a situação de meia onda é dado pela fórmula:
V
Vm = máx
π
Onde Vmáx é o valor máximo da tensão que chega à carga.
Temos:
2
VTR = E = 4 sin(100𝑡) V
5
VTRmáx − VT
3,3
Vm =
= π = 1,05 V
π
10. Para o circuito com Center Tap da figura, temos uma onda completa.
2V
Vm = πmáx
Vmáx = VTRmáx − 2VT = 2,6 V
5,2
Portanto: Vm =
= 1,66 V
π
11. Para o circuito com ponte, temos:
2V
Vm = máx
π
Vmáx = VTRmáx − 2VT = 2,6 V
Que é a mesma relação que o circuito do exercício anterior. Portanto, Vm = 1,66 V.
12. Considerando a constante de tempo do capacitor τ = RC, temos que o
descarregamento do capacitor que gerará ruído depende tanto da carga quanto da
capacitância do capacitor. Depende da carga, pois quanto menor a carga, maior a
corrente e mais rápido o descarregamento; e quanto maior o capacitor, mais carga
ele pode armazenar.
Quanto maior o tempo de descarga do capacitor, menor será Vripple (pois este é
igual a ∆V = Vmáx − V). Portanto, para valores maiores de R e C, menor é a
diferença e também Vripple .
13. Ver (12). Quanto menor R e C, maior será Vripple .
14.
15. O diodo D1 deixa apenas o sinal positivo passar. Além disso, a fonte E2 obriga o diodo
D2 a ficar em curto e funcionar sempre que o sinal no catodo estiver abaixo de 2V.
Sendo assim, a forma de onda em R1 será a forma (d).
16.
17. Para o circuito dado, Vz = 𝑉𝑅2, pois o diodo e a carga estão em paralelo. Resta então
o cálculo IZ e PZ .
Primeiro precisamos achar a corrente que chega ao resistor e ao diodo. Temos:
E−Vz
IR1 =
= 6 mA.
R1
Como IR1 = IZ + IR2 , podemos achar a corrente no diodo isolando na equação:
V
10
IZ = IR1 − IR2 , onde IR2 = R2 =
= 3,33mA
R2
3000
Portanto IZ = 2,67 mA e PZ = Vz IZ = 26,67 mW.
18. Temos novamente Vz = 𝑉𝑅2 e assim podemos descobrir a corrente que passa pelo
diodo:
V
20
IR2 = R2 =
= 16,67 mA - portanto IZ dependerá da corrente que passa por R1.
R2
1200
Para o diodo estar “ligado”, é necessário que passe corrente por ele, ou seja, IZ > 0.
Então precisamos achar a queda de tensão necessária em R1 para que passe corrente
pelo diodo. Temos então:
E−Vz
IR1 > IR2 ;
> 16,67 mA
R1
Então E > 16,67 × 10−3 R1 + Vz
E > 23,67 V.
Agora precisamos calcular o valor limite de corrente no diodo, que é o valor de
ruptura, quando sua potência ultrapassa 1200 mW.
1200 × 10−3 = 20Imáx
Imáx = 60 mA
A corrente máxima no diodo Zener encontrada é então usada para achar o valor
máximo de E para que não haja ruptura:
IR1 − IR2 < 60 mA
E − Vz
< 76,67 mA
R1
E < 76,67 × 10−3 × 220 + 20
E < 36,87 V
Portanto, 23,67 < E < 36,87 (volts)
19. Essa questão está tão mal formulada que nem entendi as condições necessárias.
Base usada na resolução dos exercícios:
Livro: Dispositivos Eletrônicos 6ed. – Boylestad
1 até 5: Capítulo 1
6: Capítulo 2, seção 2.2, exemplos 2.3 e 2.4 do Boylestad
7: Capítulo 2, seção 2.4, exemplo 2.6
8 até 13: notas de aula do Prof. Nelson
15: Capítulo 2, seções sobre retificador série/paralelo
17 e 18: Capítulo 2, seção sobre diodo Zener.