Movimento Oscilatório

MOVIMENTO OSCILATÓRIO
Força proporcional
ao deslocamento
Movimento periódico
ou oscilatório
Conservação da
energia mecânica
Movimento
harmónico simples
MOVIMENTO HARMÓNICO SIMPLES (MHS)
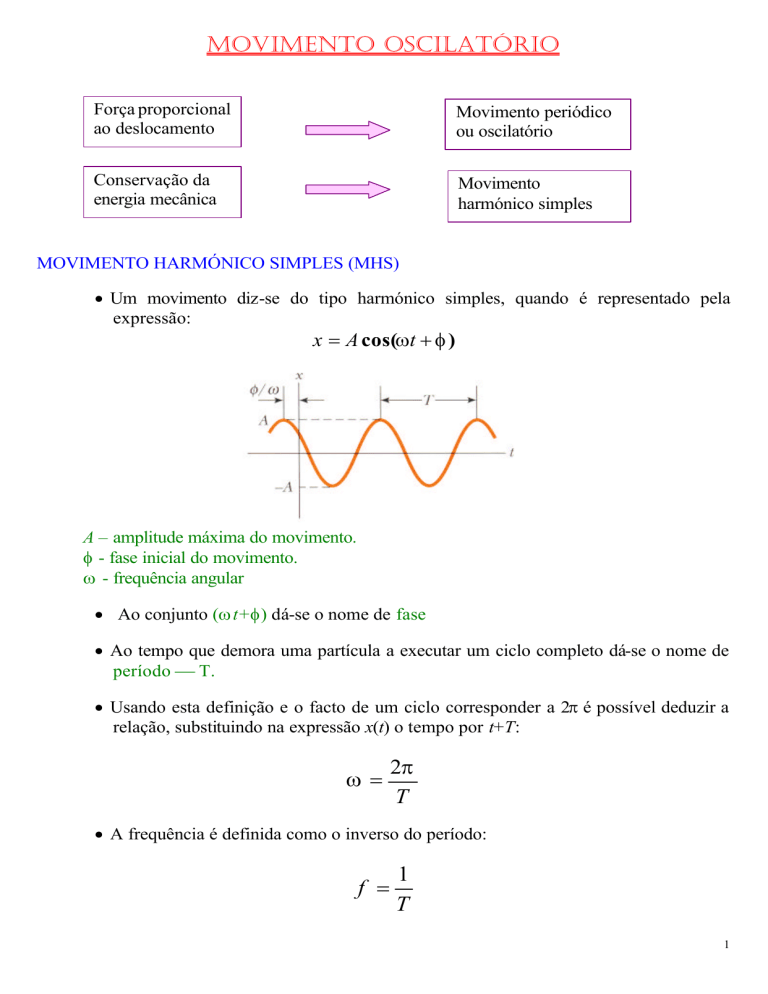
• Um movimento diz-se do tipo harmónico simples, quando é representado pela
expressão:
x = A cos(ωt + φ )
A – amplitude máxima do movimento.
φ - fase inicial do movimento.
ω - frequência angular
• Ao conjunto (ω t+φ) dá-se o nome de fase
• Ao tempo que demora uma partícula a executar um ciclo completo dá-se o nome de
período  T.
• Usando esta definição e o facto de um ciclo corresponder a 2π é possível deduzir a
relação, substituindo na expressão x(t) o tempo por t+T:
ω=
2π
T
• A frequência é definida como o inverso do período:
f =
1
T
1
• Para determinar a velocidade e a aceleração de uma partícula em MHS:
vmáx = ωA
dx
= −ωAsen(ωt + φ )
dt
dv
a=
= −ω 2 A cos(ωt + φ )
dt
v=
amáx = ω 2 A
a = −ω 2 x
• As relações de fase entre estas grandezas são dadas pelo gráfico:
• Para calcular A em função de v0, x0 e ω , usar as expressões:
x0 = A cosφ
e
v0 = −ωAsenφ
• E obtém-se:
v
tgφ = − 0
ωx0
e
v 
A = x + 0 
ω 
2
2
0
MASSA LIGADA A UMA MOLA
• Atendendo a que uma massa ligada a uma mola está sujeita a uma força:
F = −kx
e comparando com os resultados obtidos para o MHS, facilmente se conclui que, para este
sistema:
ω=
k
m
e, portanto :
T = 2π
m
k
2
• Sejam analisados dois casos distintos:
CASO I: A massa é puxada até um deslocamento x0 e largada sem velocidade inicial.
x = A cos ωt
v = − Aωsenωt
a = − Aω 2 cos ωt
CASO II: É conferida uma determinada velocidade à massa, v0, a partir da posição de
equilíbrio.
x=
v0
sen ω t
ω
v = v0 cosωt
a = −ω v0 sen ω t
• Os pêndulos simples, os estados vibracionais das moléculas, os campos
electromagnéticos podem também ser descritos, sob determinadas condições, por
este formalismo.
ENERGIA DE UMA MASSA LIGADA A UMA MOLA (OHS)
• Admitindo que não existe atrito no movimento de uma massa ligada a uma mola,
então a soma das energias cinética e potencial, mantém-se constante:
EC + E P =
1
1
mv 2 + kx 2 = c te
2
2
• Obtendo-se:
EM ( OHS ) =
1 2
kA
2
• Como resumo, poderemos usar o seguinte quadro:
t
x
v
a
EC
EP
0
A
0
-ω2 A
0
0.5kA2
T/4
0
-ωA
0
0.5kA2
0
T/2
-A
0
ω2 A
0
0.5kA2
3T/4
0
ωA
0
0.5kA2
0
T
A
0
-ω2 A
0
0.5kA2
3
MOVIMENTO OndulaTÓRIO
Ondas mecânicas
Quanto à relação entre a direcção de
propagação e a direcção da
perturbação das partículas do meio,
podem ser:
1) ondas longitudinais
2) ondas transversais
Exigem:
1) uma fonte
1)
2) um meio que possa ser perturbado
3) uma forma de ligação entre as
partículas que constituem esse meio
São caracterizadas por:
1) amplitude – deslocamento máximo das partículas
2) comprimento de onda – distância mínima entre
quaisquer dois pontos da onda que estejam no
mesmo estado
3) frequência – número de ciclos por unidade de tempo
4) velocidade de propagação da onda
Exemplo de onda longitudinal
Exemplo de onda transversal
PROPAGAÇÃO DE ONDAS A UMA DIMENSÃO
• Uma onda que se propaga tem um movimento caracterizado por uma função do tipo
(admitindo que a onda se propaga no sentido positivo do eixo), à qual se dá o nome
de função de onda:
y = f ( x − vt )
4
• Reparar que neste tipo de movimento temos a considerar duas velocidades: a
velocidade de propagação e a velocidade linear das partículas do meio.
SOBREPOSIÇÃO E INTERFERÊNCIA DE ONDAS
• Na propagação de ondas é, em geral, válido o princípio da sobreposição: “Quando
uma ou mais ondas partilham simultaneamente o mesmo espaço, a função de onda
resultante é a soma algébrica das funções de onda individuais.”. Ou seja, não existe
destruição de ondas por interferência com outras ondas.
Interferência construtiva
Interferência destrutiva
PROPAGAÇÃO DE ONDAS EM CORDAS
• A propagação de ondas em cordas obedece à expressão:
v=
T
µ , onde v é a velocidade de propagação da onda, T a tensão da corda e µ a
densidade de massa da corda por unidade de comprimento.
• Para a demonstrar atente-se na figura seguinte, admitindo que uma pequena porção da
corda pode ser aproximada a um arco de circunferência e que a aceleração, sendo
normal, será dada por v2/r. Admita-se ainda que, para ângulos pequenos, sen(α) ≅ α.
5
REFLEXÃO E TRANSMISSÃO DE ONDAS
• O aparecimento de uma fronteira na propagação de ondas pode causar reflexão total ou
parcial da energia transportada pela onda:
Exemplos de reflexão total
6
Exemplos de reflexão parcial
ONDAS SINUSOIDAIS
• Uma classe importante de ondas são as chamadas ondas sinusoidais, cuja função de
onda, quando esta se propaga segundo o sentido positivo do eixo, tem a expressão,:
 2π

y = Asen  (x − vt ) , onde A é a amplitude e λ o comprimento de onda.
λ

• Neste caso o período da onda é o tempo que a onda leva a percorrer um comprimento
de onda e, portanto, temos a relação:
v=
λ
T
• O carácter periódico da onda é evidenciado quando a função de onda toma a forma:
  x t 
y = Asen 2π  −  , y repete-se para x = nλ e para t = nT.
  λ T 
• Introduzindo as variáveis:
2π
2π
k
=
ω
=
= 2πf , a função de onda, toma a
nº de onda:
e frequência angular:
λ
T
forma:
y = A sen( kx − ω t )
• Repare-se que nas expressões anteriores y = 0, para t = 0 e para x = 0, numa situação
mais geral:
y = Asen( kx − ωt − φ )
• Reparar que, uma vez mais, é possível obter a expressão da velocidade linear das
partículas e a sua aceleração, por derivação de y.
v = − wA cos(kx − ωt − φ )
e
a = − w2 Asen( kx − ωt − φ )
7