ENG 1011 Fenômenos de Transporte I Lista de - PUC-Rio

ENG 1011 Fenômenos de Transporte I
Lista de Exercícios para P1
1. Manométria 1
Um tanque repartido contém água e mercúrio conforme mostrado
na figura. Qual é a pressão manométrica do ar preso na câmara
esquerda? A que pressão o ar da câmara esquerda deveria ser
comprimido de modo a levar a superfície da água para o mesmo
nível da superfície livre na câmara direita?
2. Manométria 2
Considere um tanque contendo mercúrio, água, benzeno
e ar conforme mostrado. Determine a pressão do ar
(manométrica = diferença de pressão entre a pressão do
ar e a pressão atmosférica). Determine o novo nível de
equilíbrio do mercúrio no manômetro, se uma abertura
for feita na parte superior do tanque.
3. Força sobre uma superfície plana submersa 1
A comporta AOC mostrada na figura tem 6 pés de largura e é articulada em O.
Desconsiderando o peso da comporta, determina a força na barra AB. A
comporta é vedada em C.
4. Força sobre uma superfície plana submersa 2
A comporta mostrada na figura tem 3 metros de largura e, para fins de
análise, pode ser considerada sem peso. Para qual profundidade de água
esta comporta retangular ficará em equilíbrio como mostrado?
5. Força sobre uma superfície plana submersa 3
Um longo bloco de madeira, de seção quadrada, é articulado
em uma de suas arestas. O bloco está em equilíbrio quando
imerso em água a profundidade de água mostrada. Avalie a
densidade relativa da madeira se o atrito no pivô desprezível.
6. Força sobre uma superfície plana submersa 4
Uma comporta retangular (largura W = 2m) é articulada
conforme mostrado, com um batente na borda interior. Em que
profundidade H a comporta estará prestes a abrir?
7. Força sobre uma superfície plana submersa 5
Uma comporta plana semicircular AB é articulada ao longo
de B e suportada pela força horizontal FA aplicada em A. O
liquido à esquerda da comporta é água. Calcule a força FA
requerida para o equilíbrio.
8. Empuxo
Um cilindro flutua na água como mostrado. Qual é a sua
densidade relativa?
9. Conservação de massa 1
No escoamento incompressível através do dispositivo mostrado, as
velocidades podem ser consideradas uniformes em todas as seções de
entrada e de saída. As seguintes condições são conhecidas: A1 = 0,1m², A2
= 0,2m², A3 = 0,15m², V1 = 10exp(-t/2) m/s e V2 = 2cos(2πt) m/s (t em
segundos). Obtenha uma expressão para a velocidade na seção 3 e trace
um gráfico de V3 como uma função do tempo. Em que instante V3 tornase zero pela primeira vez? Qual é a vazão volumétrica total média na seção 3?
10. Conservação de massa 2
Água escoa em regime permanente através de um tubo de comprimento L e raio R = 75 mm. Calcule a
velocidade uniforme na entrada, U, se a distribuição de velocidades na saída é dada por:
11. Conservação de massa 3
Água escoa em regime permanente sobre uma placa
porosa. Uma sucção constante é aplicada ao longo da
seção porosa. O perfil de velocidade na seção cd é:
Avalie a vazão mássica através da seção bc.
12. Segunda lei de Newton 1
Um tanque, de altura h = 1 m e diâmetro D = 0,6 m, está fixo a um
carrinho, como mostrado na figura. Água jorra do tanque através de um
bocal de diâmetro d= 10 mm. A velocidade uniforme do líquido saindo do
tanque é de aproximadamente
, onde y é a distância vertical do
√
bocal até a superfície livre do líquido. Determine a tração no cabo para y
= 0,8 m. Trace um gráfico da tensão no cabo em função da profundidade
de água para a faixa 0 ≤ y ≤ 0,8 m.
13. Segunda lei de Newton 2
A figura mostra um redutor em uma tubulação o volume
interno do redutor é 0,2 m3 e sua massa é 25 kg. Avalie a
força total de reação que deve ser feita pelos tubos adjacentes
para suportar o redutor. O fluido é gasolina.
14. Segunda lei de Newton 3
Ar entra em um duto, de diâmetro D = 25 mm, através de
uma entrada bem arredondada com velocidade uniforme, U1
= 0,870 m/s. Em uma seção a jusante, onde L = 2,25 m, o
perfil de velocidade inteiramente desenvolvido é:
A queda de pressão entre essas seções é p1-p2 = 1,92 N/m². Determine a força total de atrito exercida pelo
tubo sobre o ar.
15. Segunda lei de Newton 4
Uma máquina típica para testes de motores a jato é
mostrada na figura, juntamente com alguns dados de
testes. O combustível entra verticalmente no topo da
máquina a uma taxa igual a 2% da vazão em massa do
ar de admissão. Para as condições dadas, calcule a
vazão em massa de ar através da máquina e estime o empuxo produzido.
Obs: psfg = pounds-force per square foot (gauge) – pressão manométrica em libra-força por pé quadrado.
16. Segunda lei de Newton 5
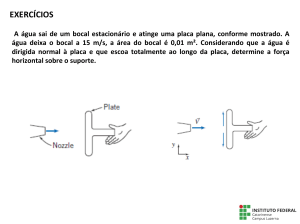
O bocal mostrado descarrega uma cortina de água num arco de
180°. A uma distância radial de 0,3 m a partir da linha de centro do
tubo de suprimento, a velocidade da água é 15 m/s e a espessura do
jato é 30 mm. Determine (a) a vazão volumétrica da cortina de água
que entra pelo tubo de suprimento de diâmetro D, onde a pressão
absoluta é p1 = 100 kPa (manométrica) e (b) os componentes x, y e
z da força necessária para manter o bocal estacionário.
Dados / Formulário:
Respostas:
1) p = 3,48 kPa (manométrica);
p = 123 kPa (manométrica).
9) t = 2,39 s; Qtotal = 2 m3.
10) U = 1,5 m/s.
2) pair = 24,7 kPa (monométrica); h = 0,116 m.
11) ̇
3) FAB = 1800 lbf.
12) T = 1,23 N.
4). d = 2,66 m.
13) ⃗
5) Densidade relativa = 0,542.
14) F = 7,90.10-4 N
6) H = 2,17 m.
15) T = 65200 lbf.
7) FA = 366 kN.
16) Q = 0,424 m3/s; Fx = 0 kN; Fy = 4,05 kN;
8) d = ¾.
= 1,42 kg/s (para fora).
̂
Fz = 6,53 kN.
̂ kN.