Teoria - Unesp

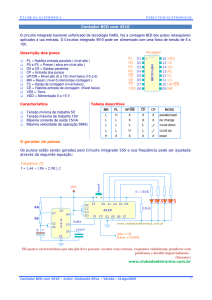
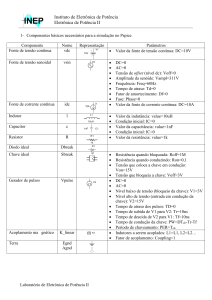
Cap. 6 - Cicloconversores
99
CAPÍTULO - 6
CICLOCONVERSORES
6.1 - INTRODUÇÃO
) OBJETIVO: CONVERSÃO ESTÁTICA DIRETA CA/CA DE UMA DADA
FREQÜÊNCIA PARA OUTRA FREQÜÊNCIA INFERIOR.
(NÃO HÁ ESTÁGIO INTERMEDIÁRIO DE CORRENTE CONTÍNUA)
) APLICAÇÕES:
A) ACIONAMENTO DE MOTORES CA (SÍNCRONOS e INDUÇÃO)
FREQÜÊNCIA FIXA DA REDE ⇒ FREQÜÊNCIA VARIÁVEL
(CONTROLE VELOCIDADE MOTOR DE INDUÇÃO OU SÍNCRONO)
b) AERONAVES
OBTENÇÃO DE FREQÜÊNCIA CONSTANTE A PARTIR DE UM
ALTERNADOR DE VELOCIDADE VARIÁVEL (FREQÜÊNCIA
VARIÁVEL).
6.2 - PRINCÍPIO DE FUNCIONAMENTO
) SEJA A ESTRUTURA DA FIGURA 6.1 (CONVERSOR DUAL 3 PULSOS)
„ CONSIDERA-SE CARGA INDUTIVA (CONDUÇÃO CONTÍNUA)
v1(ωt)
v2(ωt)
v3(ωt)
T1
P
N
T2
T3
T4
T5
iL
vL
T6
Fig. 6.1 - Cicloconversor monofásico de 3 pulsos.
) TENSÃO MÉDIA PARA O RETIFICADOR 3 PULSOS:
VLmed = 1,17 Vo cos α
) FUNÇÃO DE CONTROLE DO CICLOCONVERSOR 3 PULSOS
cos α = F ( t )
) PORTANTO:
(6.1)
VLmed = 1,17 Vo F ( t )
„ TENSÃO MÉDIA NA CARGA É PROPORCIONAL À FUNÇÃO F(t)
Eletrônica Industrial-Eletrônica de Potência
(6.2)
Cap. 6 - Cicloconversores
100
) EXEMPLO DE CONTROLE - FORMAS DE ONDA (FIG. 6.2)
F(t)
T/2
T/2
(a)
+1
α p=0
ο
ωt
α p=180
ο
-1
vL
ο
α p=0
ο
α n=180
v1
v2
v3
v1
ο
α p=180
ο
α n=0
v2
v3
v1
v2
v3
v1
v2
v3
v1
v2
v3
(b)
ωt
Fig. 6.2 - Formas de onda num cicloconversor: (a)Função de controle e (b)Tensão na
carga.
) CONCLUSÃO:
ESTRUTURA CONVERSOR DUAL ⇒ CICLOCONVERSOR
(COM COMANDO ADEQUADO)
) FUNÇÃO:
CONVERTER UMA TENSÃO ALTERNADA EM OUTRA COM
FREQÜÊNCIA DIFERENTE.
„ SEJA F(t) VARIANDO SENOIDALMENTE (Fig. 6.3)
(a)
F(t)
T/2
ωt
T/2
(b)
vL
ωt
Retificação
iL
φ
Inversão
(c)
Corrente no
Grupo Positivo
ωt
Corrente no
Grupo Negativo
Fig. 6.3 - Formas de onda cicloconversor 3 pulsos monofásico: (a)Função de controle,
(b)Tensão na carga e (c)Corrente fundamental na carga.
) φ= ÂNGULO ATRASO DA FUNDAMENTAL DA CORRENTE EM
RELAÇÃO À FUNDAMENTAL DA TENSÃO NA CARGA ⇒ CARGA
INDUTIVA.
Eletrônica Industrial-Eletrônica de Potência
Cap. 6 - Cicloconversores
101
) CICLO DE FUNCIONAMENTO:
vL
+
+
iL
+
+
-
Grupo P
Retificador
Inversor
-
Grupo N
Retificador
Inversor
) REPRESENTAÇÃO ESQUEMÁTICA - CICLOCONVERSOR (FIG. 6.4)
v1 ( ω t )
v2 ( ω t )
v3 ( ω t )
T1
T2
GRUPO P
T4
T3
L/2
L/2
+
vL
-
N
Z
T5
T6
GRUPO N
Z
iL
N
(a)
(b)
Fig. 6.4 - Cicloconversor monofásico de 3 pulsos, (a)Topologia e (b)Representação.
6.3 - EQUAÇÃO DA TENSÃO DE SAÍDA ⇒ F(t) variando senoidalmente
) α = 0 ⇒ TENSÃO MÉDIA PRODUZIDA POR UM GRUPO (Equação 6.3).
VLo = 2 Vo
π
m
sen 
π
m
(6.3)
„ ONDE: Vo - VALOR EFICAZ TENSÃO DE ENTRADA
m - NÚMERO DE PULSOS.
VLo - TENSÃO MÉDIA MÁXIMA NA CARGA (α = 0).
) α = 0 ⇒ TENSÃO EFICAZ PRODUZIDA POR UM GRUPO (Equação 6.4).
π
m
sen 
π
m
π
m
= 2 Vo
sen  
π
m
VLM = Vo
„ ONDE:
2 VLM
(6.4)
VLM - TENSÃO EFICAZ MÁXIMA NA CARGA (α = 0).
„ OBS: (a)SÃO IGNORADAS AS QUEDAS DE TENSÃO INTERNAS.
(COMPONENTES E SOBRETUDO AQUELAS DEVIDO À COMUTAÇÃO;
(b)ÂNGULO αP NÃO PODE SER NULO NA PRÁTICA (αN = 180o).
A COMUTAÇÃO NÃO É INSTANTÂNEA ⇒ ÂNGULO αN DEVE SER
SEMPRE INFERIOR A 180O.
„ αPmin > 0 ⇒ TENSÃO EFICAZ NA CARGA (POR GRUPO) (Equação 6.5).
VLM = Vo
π
m
⋅ sen  ⋅ cos α min
π
m
Eletrônica Industrial-Eletrônica de Potência
(6.5)
Cap. 6 - Cicloconversores
102
6.4 - ESTRUTURAS DOS CICLOCONVERSORES
) EM GERAL AS TENSÕES DE ENTRADA SÃO TRIFÁSICAS E
BALANCEADAS.
) TENSÕES DE SAÍDA PODEM SER MONOFÁSICAS OU TRIFÁSICAS.
) UM AUMENTO DO NÚMERO DE PULSOS REDUZ O CONTEÚDO
HARMÔNICO DAS TENSÕES DE SAÍDA.
) MAIOR NÚMERO DE PULSOS IMPLICA EM MAIOR NÚMERO DE
TIRISTORES, O QUE AUMENTA O CUSTO DA MONTAGEM.
(a)CICLOCONVERSOR TRIFÁSICO DE 3 PULSOS (FIGURA 6.5).
Io
2
Rede
- Vo +
VLM= 3 3Vo
2π
+
VLM R Io
-
S Io
T Io
Circuito A
Fig. 6.5 - Cicloconversor de 3 pulsos com ponto médio.
(b)CICLOCONVERSOR TRIFÁSICO DE 6 PULSOS (FIGURAS 6.6 e 6.7).
(NECESSIDADE DE ISOLAMENTO NA ENTRADA OU NA SAÍDA)
Io
2
Rede
-
Vo +
VLM=3 3Vo
π
+
VLM R Io
S
Io
T Io
-
Circuito B
Fig. 6.6 - Cicloconversor de 6 pulsos, em ponte, paras cargas isoladas.
Eletrônica Industrial-Eletrônica de Potência
Cap. 6 - Cicloconversores
103
Io
2
- Vo +
Rede
- Vo +
- Vo +
VLM = 3 3 Vo
π
+
VLM R
-
T
S
Io
Io
Io
Circuito C
Fig. 6.7 - Cicloconversor de 6 pulsos, em ponte, paras cargas não isoladas.
) SOLUÇÃO MAIS ECONÔMICA (FIGURA 6.6)
„ ENTRADA É COMUM AOS 3 GRUPOS E A SAÍDA É ISOLADA.
„ RECOMENDADO PARA A
TRIFÁSICAS
DE
CORRENTE
ESTATÓRICOS ISOLADOS).
ALIMENTAÇÃO DE MÁQUINAS
ALTERNADA
(ENROLAMENTOS
„ TRANSFORMADOR PODE SER EXCLUÍDO (NECESSÁRIO SOMENTE
PARA ADAPTAÇÃO DA TENSÃO DE ALIMENTAÇÃO.
) CASO EM QUE AS TRÊS FASES DA CARGA NÃO POSSAM SER
ISOLADAS ENTRE SI (FIGURA 6.7):
„ NECESSÁRIO O EMPREGO DE UM TRANSFORMADOR COM 3
SAÍDAS ISOLADAS.
„ CAPACIDADE TOTAL EM VA DO SECUNDÁRIO DEVE SER 22%
MAIOR QUE A DO PRIMÁRIO.
) RELAÇÕES QUANTITATIVAS (TABELA 1)
„ Dimensionamento dos transformadores.
„ Cálculo das correntes, potência ativa e reativa.
Tabela 1 - Relações Quantitativas Básicas dos Cicloconversores (*)
r
Ni
cos φi
1,32 (3 VLM I o )
1,0
0,843
1,32 (3 VLM I o )
0,1
0,078
1,21 (3 VLM I o )
1,0
0,843
1,32 (3 VLM I o )
0,1
0,078
1,21 (3 VLM I o )
1,0
0,843
1,32 (3 VLM I o )
0,1
0,078
(*) cos φi válido para cos φi = 1
Circuito
A
B
C
Eletrônica Industrial-Eletrônica de Potência
NP
1,32 (3 VLM I o )
1,32 (3 VLM I o )
1,21 (3 VLM I o )
1,32 (3 VLM I o )
1,21 (3 VLM I o )
1,32 (3 VLM I o )
NS
1,32 (3 VLM I o )
1,32 (3 VLM I o )
1,21 (3 VLM I o )
1,32 (3 VLM I o )
1,48 (3 VLM I o )
1,48 (3 VLM I o )
Cap. 6 - Cicloconversores
104
„ ONDE:
) r = cos α (IMPÕE A AMPLITUDE DA FUNDAMENTAL DA TENSÃO NA
SAÍDA).
)
)
)
)
)
)
Ni = POTÊNCIA APARENTE TOTAL NA ENTRADA DO CIRCUITO.
NP = POTÊNCIA APARENTE TOTAL NO PRIMÁRIO DO TRAFO.
NS = POTÊNCIA APARENTE TOTAL NO SECUNDÁRIO DO TRAFO.
Io = CORRENTE EFICAZ NA CARGA.
cos φi = FATOR DE DESLOCAMENTO DA ENTRADA.
cos φo = FATOR DE DESLOCAMENTO DA CARGA.
) VLM =
3 3 Vo
(Estrutura A)
2π
) VLM =
3 3 Vo
π
(Estruturas B E C)
) Vo = VALOR EFICAZ DA TENSÃO FASE-NEUTRO NO SECUNDÁRIO
DO TRAFO.
) VLM = VALOR EFICAZ MÁXIMO DA TENSÃO FASE-NEUTRO NA
CARGA.
6.5 - HARMÔNICAS DA TENSÃO DE SAÍDA
6.5.1 - Freqüências das Harmônicas
) CICLOCONVERSORES COM CORRENTE DE CIRCULAÇÃO.
a) CONVERSOR DE 3 PULSOS
f H = 3 ( 2p − 1) f i ± 2n f o
(6.6)
n ≤ 3 ( 2p − 1) + 1
„ Com:
(6.7)
„ Onde: p - NÚMERO INTEIRO DE 1 a ∞.
n - NÚMERO INTEIRO DE 0 a ∞ (no Harmônico)
fH - FREQÜÊNCIA DAS HARMÔNICAS.
fi - FREQÜÊNCIA DE ALIMENTAÇÃO.
fo- FREQÜÊNCIA DE SAÍDA DO CICLOCONVERSOR.
b) CONVERSOR DE 6 PULSOS
„ Onde:
f H = 6p fi ± ( 2n + 1) fo
( 2n + 1) ≤ ( 6p + 1)
(6.8)
(6.9)
c) CONVERSOR DE 12 PULSOS
„ Onde:
f H = 12p fi ± ( 2n + 1) fo
( 2n + 1) ≤ (12p + 1)
(6.10)
(6.11)
) FREQÜÊNCIAS DAS HARMÔNICAS DA TENSÃO DE SAÍDA
DEPENDEM:
„ NÚMERO
DE
PULSOS
(ESTRUTURA
CICLOCONVERSOR;
„ FREQÜÊNCIA DAS TENSÕES DE ENTRADA,
„ FREQÜÊNCIA DAS TENSÕES DE SAÍDA.
Eletrônica Industrial-Eletrônica de Potência
DE
BASE)
DO
Cap. 6 - Cicloconversores
105
) PRESENÇA DE SUBHARMÔNICAS (Equação 6.12 e Figura 6.8)
fH
f
= 3 ( 2p − 1) i ± 2n
fo
fo
„ COM:
p=1en=3 ⇒
(6.12)
6f
fH
= 3± o
fi
fi
(6.13)
„ SUBHARMÔNICAS ⇒ 1/3 < fo/fi < 2/3
fH
fi
5
4
1 3+6fo
fi
2 3−6fo
fi
1
3
2
1
SubHar
mônicos
0
0
2
2
Curva
Desejada
fo
1,0 f
i
Fig. 6.8 - Freqüências das harmônicas da tensão de saída, cicloconversor de 3 pulsos.
0,2
0,3330,4
0,6
0,8
) RESTRIÇÕES:
A) CORRENTE DE CIRCULAÇÃO;
B) MODULAÇÃO DO ÂNGULO DISPARO (α) DEVE SER COSSENOIDAL,
c) CORRENTE NA CARGA DEVE SER EM CONDUÇÃO CONTÍNUA (não
deve haver descontinuidade na corrente de carga).
6.5.2 - AMPLITUDES DAS HARMÔNICAS DA TENSÃO DE CARGA
) NÃO DEPENDEM DO FATOR DE POTÊNCIA DA CARGA.
) DEPENDEM DO VALOR DA TENSÃO DE SAÍDA EM RELAÇÃO AO SEU
PRÓPRIO VALOR MÁXIMO ⇒ DEPENDEM DE r = cos α (Fator de Modulação).
„ AMPLITUDES PREDOMINANTES OCORREM PARA p = 1, (Equações 6.14, 6.15 e
6.16).
(a) 3 PULSOS:
f H = 3 f i ± 2n f o
, Para n ≤ 4
(6.14)
(b) 6 PULSOS:
f H = 6 f i ± ( 2n + 1) f o
, Para n ≤ 3
(6.15)
(c) 12 PULSOS:
f H = 12 f i ± ( 2n + 1) f o
,Para n ≤ 6
(6.16)
Eletrônica Industrial-Eletrônica de Potência
Cap. 6 - Cicloconversores
106
) AMPLITUDES HARMÔNICAS (TABLEAS 2 e 3)
„ VALORES EM (PU) ⇒ Vbase =
2 VLM
Tabela 2 - Amplitudes das Harmônicas da Tensão de Carga para os Cicloconversores de 3
Pulsos
f H = 3 f i ± 2n f o
n
0
1
2
r
1,0
0,000
0,250
0,125
0,9
0,027
0,279
0,082
0,8
0,097
0,275
0,051
0,7
0,195
0,247
0,030
0,6
0,307
0,205
0,016
0,5
0,422
0,156
0,008
0,4
0,529
0,107
0,003
0,3
0,621
0,063
0,001
0,2
0,691
0,029
0,000
0,1
0,735
0,007
0,000
Tabela 3 - Amplitudes das Harmônicas da Tensão de Carga para os Cicloconversores de 6
Pulsos
f H = 6 f i ± ( 2n + 1) f o
n
0
1
2
3
r
1,0
0,000
0,000
0,100
0,071
0,9
0,033
0,039
0,115
0,034
0,8
0,062
0,100
0,092
0,015
0,7
0,041
0,134
0,060
0,006
0,6
0,025
0,133
0,033
0,002
0,5
0,105
0,105
0,015
0,001
0,4
0,169
0,068
0,005
0,000
0,3
0,193
0,034
0,001
0,000
0,2
0,166
0,011
0,000
0,000
0,1
0,096
0,001
0,000
0,000
) PARA: fo = 0 ⇒ Freqüências fundamentais (cicloconversores de 3 e 6 pulsos)
fH = 3 fi
são, respectivamente:
(6.17)
fH = 6 fi
(6.18)
(QUE SÃO AS HARMÔNICAS FUNDAMENTAIS DOS RETIFICADORES SIMPLES).
6.6 - LIMITES DA FREQÜÊNCIA DE SAÍDA
) FREQÜÊNCIAS DAS HARMÔNICAS DAS TENSÕES DE SAÍDA (fH)
DEPENDEM DA FREQÜÊNCIA DE SAÍDA fO.
) CERTOS VALORES DE fH DIMINUEM COM O AUMENTO DE fO.
(DIFICULDADES DE FILTRAGEM).
„ LIMITAÇÃO (CICLOCONVERSORES 3 PULSOS) RECOMENDA-SE:
fo ≤
Eletrônica Industrial-Eletrônica de Potência
fi
3
(6.19)
Cap. 6 - Cicloconversores
107
6.7 - CORRENTES DE ENTRADA DOS CICLOCONVERSORES
) COMPONENTES DA CORRENTE EM UMA FASE DO CICLOCONVERSOR:
a) Id - COMPONENTE ATIVA, RESPONSÁVEL PELA TRANSFERÊNCIA DE
POTÊNCIA DA FONTE PARA A CARGA.
b) Iq - COMPONENTE EM QUADRATURA OU REATIVA (DEPENDE DO
FATOR DE POTÊNCIA DA CARGA E DE cos α).
c) ΣIh - COMPONENTE QUE REÚNE O CONJUNTO DE HARMÔNICAS.
) VALOR EFICAZ DA CORRENTE DE ENTRADA (Equação 6.20)
I ef = I d 2 + I q 2 + ΣI h 2
(6.20)
„ OBS: MESMO COM FATOR DE POTÊNCIA NA CARGA UNITÁRIO ⇒ Iq ≠ 0,
„ HARMÔNICAS REDUZEM FATOR DE POTÊNCIA
(PORTANTO, FATOR DE POTÊNCIA DA ENTRADA < 1 - SEMPRE)
) FATOR DE DESLOCAMENTO ENTRADA (cos φi)
cosφ i =
Id
(6.21)
Id2 + Iq2
(DEPENDE DO FATOR DE POTÊNCIA DA CARGA e de r= cos α)
) VALOR EFICAZ DA FUNDAMENTAL DE CORRENTE NA ENTRADA:
I1 = Id 2 + Iq 2
cosφ i =
„ PORTANTO:
(6.22)
Id
I1
(6.23)
) FATOR DE POTÊNCIA APRESENTADO À REDE (Equação 6.24)
FP =
cos φ i
Po
Ni
(6.24)
1,0
0,9
0,843
0,8
r = 1,0
0,7
r = 0 ,8
0,6
r = 0 ,7
0,5
r = 0 ,6
r = 0 ,9
r = 0 ,5
0,4
r = 0 ,4
0,3
r = 0 ,3
0,2
r = 0 ,2
0,1
r = 0 ,1
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
cos φ o
1,0
Fig. 6.9 - Fator de deslocamento entrada em função do fator de deslocamento da
carga, tomando r como parâmetro, para todos os cicloconversores estáticos.
Eletrônica Industrial-Eletrônica de Potência
Cap. 6 - Cicloconversores
108
6.8 - FREQÜÊNCIAS DAS HARMÔNICAS DA CORRENTE DE ENTRADA
A) HARMÔNICAS CARACTERÍSTICAS
)(INDEPENDEM DA CONFIGURAÇÃO OU DO NÚMERO DE PULSOS)
A.1) PARA SAÍDA MONOFÁSICA
f H = f i ± 2n f o
(6.25)
A.2) PARA SAÍDA TRIFÁSICA
f H = fi ± 2n fo
(6.26)
„ Onde:
n - 1, 2, 3, 4, ...., ∞
fi - FREQÜÊNCIA DE ENTRADA.
fo- FREQÜÊNCIA DE SAÍDA (CARGA).
fH - FREQÜÊNCIA DAS HARMÔNICAS NA CARGA.
B) HARMÔNICAS DEPENDENTES DA CONFIGURAÇÃO
B.1) CICLOCONVERSOR DE 3 PULSOS
B.1.1) SAÍDA MONOFÁSICA
f H = [ 3 ( 2p − 1) ± 1] fi ± ( 2n + 1) fo
(6.27)
f H = ( 6p ± 1) fi ± 2n fo
(6.28)
B.1.2) SAÍDA TRIFÁSICA BALANCEADA
f H = [ 3 ( 2p − 1) ± 1] fi ± 3 ( 2n + 1) fo
(6.29)
f H = ( 6p ± 1) fi ± 6n fo
(6.30)
„ Onde:
p - 1, 2, 3, 4, ...., ∞
n - 0, 1, 2, 3, ...., ∞
B.2) CICLOCONVERSOR DE 6 PULSOS
B.2.1) SAÍDA MONOFÁSICA
f H = ( 6p ± 1) fi ± 2n fo
(6.31)
B.2.2) SAÍDA TRIFÁSICA BALANCEADA
f H = ( 6p ± 1) fi ± 6n fo
Eletrônica Industrial-Eletrônica de Potência
(6.32)