matemática ii

7
PROVA DE FÍSICA II
QUESTÃO 16
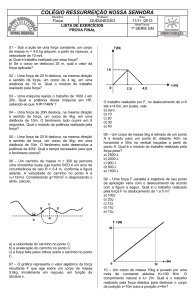
Uma barra homogênea de massa 4,0 kg e comprimento 1,0 m está apoiada em suas extremidades
sobre dois suportes A e B conforme desenho abaixo. Coloca-se a seguir, apoiada sobre a barra, uma
esfera maciça, de massa 2,0 kg, a 20 cm do apoio B. Admitindo-se g = 10m/s2, pode-se afirmar que
as forças que os apoios A e B fazem sobre a barra valem respectivamente:
a)
b)
c)
d)
25 N e 35 N
40 N e 60 N
24 N e 36 N
30 N e 30 N
QUESTÃO 17
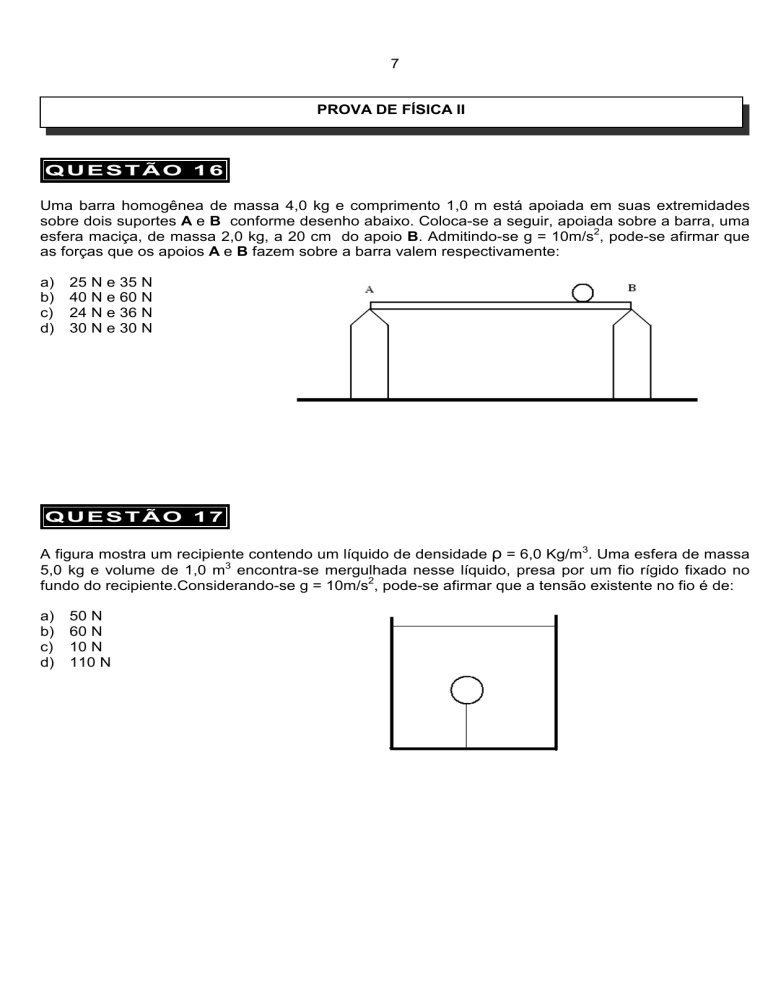
A figura mostra um recipiente contendo um líquido de densidade ρ = 6,0 Kg/m3. Uma esfera de massa
5,0 kg e volume de 1,0 m3 encontra-se mergulhada nesse líquido, presa por um fio rígido fixado no
fundo do recipiente.Considerando-se g = 10m/s2, pode-se afirmar que a tensão existente no fio é de:
a)
b)
c)
d)
50 N
60 N
10 N
110 N
8
AS QUESTÕES 18 E 19 REFEREM-SE À SITUAÇÃO A SEGUIR. NA FIGURA, O BLOCO A TEM
UMA MASSA MA = 80kg E O BLOCO B, UMA MASSA MB = 20kg. SÃO AINDA DESPREZÍVEIS OS
ATRITOS E AS INÉRCIAS DO FIO E DA POLIA E CONSIDERA-SE g= 10m/s2.
QUESTÃO 18
Sobre a aceleração do bloco B, pode-se afirmar que ela será de:
a)
b)
c)
d)
10 m/s2 para baixo.
4,0 m/s2 para cima.
4,0 m/s2 para baixo.
2,0 m/s2 para baixo.
QUESTÃO 19
O módulo da força que traciona o fio é:
a)
b)
c)
d)
160 N
200 N
400 N
600 N
QUESTÃO 20
Uma locomotiva puxa uma composição de vagões e, por certo intervalo de tempo, exerce uma força
de 1,0 x 10 5N, mantendo, em um trecho retilíneo, a velocidade da composição constante em 10m/s.
Nessa situação, a potência dissipada pelas forças de atrito é de:
a)
b)
c)
d)
4,0 x 105 W
1,0 x 106 W
1,0 x 105 W
5,0 x 106 W
9
AS QUESTÕES 21 E 22 REFEREM-SE AO DESENHO ABAIXO, QUE MOSTRA UM CONDUTOR
RETILÍNEO LONGO DE RESISTÊNCIA ELÉTRICA R = 3Ω
Ω LIGADO A UMA FONTE DE 12,0 V.
PRÓXIMO EXISTE UM SEGUNDO CONDUTOR DE COMPRIMENTO 10 cm, PERCORRIDO POR
UMA CORRENTE DE 0,1 A, PARALELO AO PRIMEIRO. O SENTIDO DA CORRENTE NO CONDUTOR 2 ESTÁ INDICADO NA FIGURA.
Dado: µ 0 = 4π x 10 −7
N
A2
QUESTÃO 21
Assinale o valor do campo magnético criado pelo condutor 1 a uma distância de 1 cm, no local onde
se encontra o condutor 2.
a)
b)
c)
d)
B = 8 x 10−6T
B = 8 x 10−5T
B = 16 π x 10−7T
B = 32 π x10−4T
QUESTÃO 22
A força do campo magnético sobre o condutor 2 é de:
a)
b)
c)
d)
8 π x 10−7 N para a direita
6 x 10−5 N para a esquerda
8 x 10−7 N para a esquerda
12 x 10−4 N para cima
10
QUESTÃO 23
A figura mostra um campo elétrico uniforme e três superfícies equipotenciais, representadas por A, B e
C. Considerando-se o módulo do campo elétrico como 4,0 x 102 V/m, então o trabalho necessário para
se levar uma carga q= 1,0 x 10-6C do ponto 2 até o ponto 6 pela trajetória retilínea 2 5 6 será de :
2
E = 4,0 x 10 V/m
a)
b)
c)
d)
W
W
W
W
= 4,0 x 10−4J
= 1,0 x 10−4J
= 6,0 x 10−5J
= 8,0 x 10−5J
AS QUESTÕES 24 E 25 REFEREM-SE À SITUAÇÃO DESCRITA A SEGUIR.
Um bloco de massa 3,0 kg é pressionado contra uma parede
vertical por uma força F conforme ilustração. Considere a gravidade como 10m/s2, o coeficiente de atrito estático entre o
bloco e a parede como 0,20 e o coeficiente de atrito cinético
como 0,15.
QUESTÃO 24
O valor mínimo da força F para que o bloco permaneça em equilíbrio estático é de:
a)
b)
c)
d)
150 N
125 N
90 N
80 N
11
QUESTÃO 25
O valor máximo da força F para que o bloco desça em equilíbrio dinâmico é de:
a)
b)
c)
d)
125 N
200 N
250 N
150 N
QUESTÃO 26
Os gatos conseguem sair ilesos de muitas quedas. Suponha que a maior velocidade que ele possa
atingir o solo, sem se machucar, seja de 29 Km/h. Então, desprezando-se a resistência do ar e considerando g = 10m/s2, a altura máxima de queda para que um gato, partindo do repouso, nada sofra é,
aproximadamente, de:
a)
b)
c)
d)
6,4 m
10 m
2,5 m
3,2 m
RESPONDA ÀS QUESTÕES 27 E 28 DE ACORDO COM AS INFORMAÇÕES A SEGUIR.
O gráfico mostra a velocidade como função do tempo de dois objetos em movimento retilíneo, que partem da mesma posição.
QUESTÃO 27
As acelerações dos móveis A e B no instante t = 2,5 s valem respectivamente:
a)
b)
c)
d)
5 m/s2 e 4 m/s2
2,4 m/s2 e 0,8 m/s2
10 m/s2 e 8 m/s2
0 e 0,6 m/s2
12
QUESTÃO 28
O instante em que os móveis A e B novamente se encontram será aproximadamente:
a)
b)
c)
d)
t = 10 s
t = 0,4 s
t = 4,8 s
t = 2,5 s
AS QUESTÕES 29 E 30 BASEIAM-SE NO TEXTO A SEGUIR.
A fabulosa quantidade de energia que o Sol irradia continuamente para o espaço pode ser analisada
através da equação E = ∆mc2 . Os cientistas acreditam que essa energia solar tem sua origem em
reações nucleares, nas quais 4 átomos de Hidrogênio se unem para formar um átomo de Hélio, reações essas que são acompanhadas de uma grande emissão de energia. Uma reação como esta, em
que núcleos leves se unem originando um núcleo mais pesado, é denominada fusão nuclear.Verificase que a massa do Hélio formada é de 6,646 x 10-27 kg e é inferior à soma das massas dos 4 núcleos
de Hidrogênio, que somadas resultam em 6,694 x 10-27 kg. Portanto, a energia dessa fusão é função
desta redução de massa, podendo ser calculada pela fórmula que relaciona massa (∆m) com energia
(E) dada acima, considerando-se a velocidade da luz c = 3,0 x 10 5 km/s. Estima-se que no Sol ocorrem 1038 reações desse tipo em cada segundo.
( Adaptado de Curso de Física, de Beatriz Alvarenga e Antonio Máximo)
QUESTÃO 29
Tendo em vista o texto dado, pode-se calcular a energia liberada pelo Sol em uma reação e a potência
irradiada pelo Sol.Os valores dessas duas grandezas serão respectivamente iguais a:
a)
b)
c)
d)
1,20
1,20
4,32
4,32
x
x
x
x
10−9 J
10−9 J
10−12J
10−12J
e
e
e
e
1,20 x 1024 W
1,20 x 1029 W
4,32 x 1024 W
4,32 x 1026 W
QUESTÃO 30
Considere que uma molécula de H2 receba uma energia igual à liberada pelo Sol em uma reação de
fusão e que toda essa energia seja convertida em movimento da molécula.Se a massa da molécula de
H2 é de aproximadamente 3,0 x 10−27 kg, então velocidade dessa molécula após receber essa energia
será de:
a) 2,88 x 1015 m/s
b) 1,44 x 1015 m/s
c) [2,88 x 1015](1/2) m/s
d) [1,88 x 1012](1/2) m/s