Faça desse arquivo para visualizar os objetos.

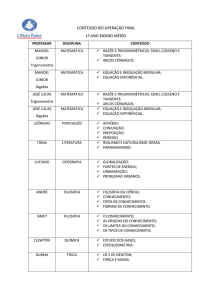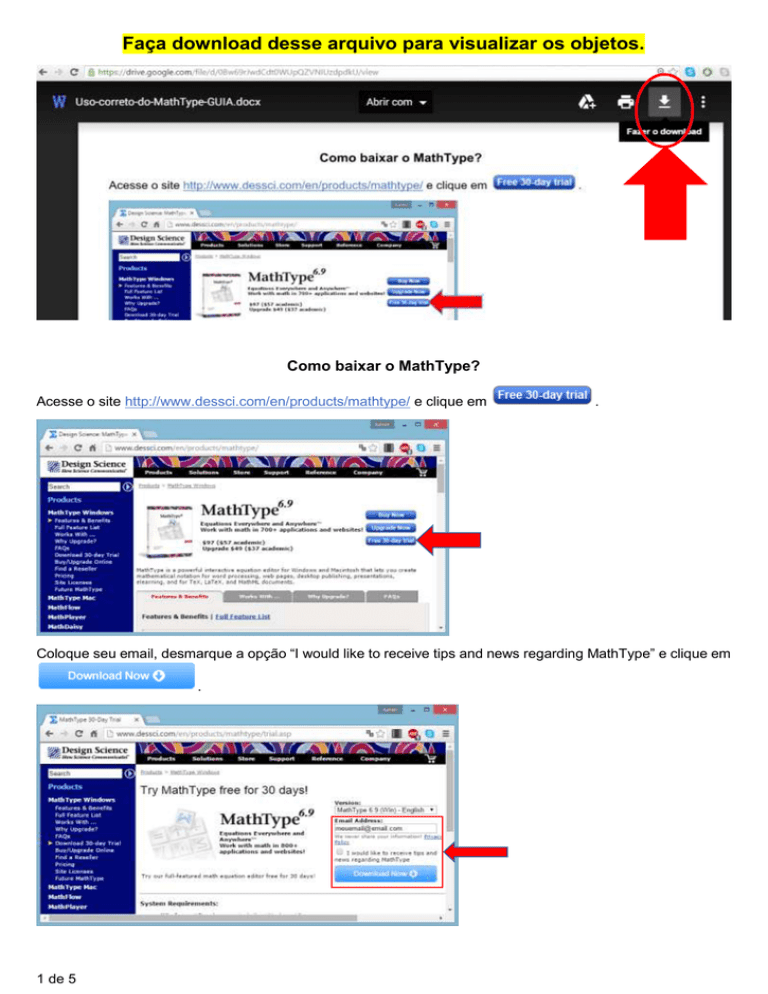
Faça download desse arquivo para visualizar os objetos.
Como baixar o MathType?
Acesse o site http://www.dessci.com/en/products/mathtype/ e clique em
.
Coloque seu email, desmarque a opção “I would like to receive tips and news regarding MathType” e clique em
.
1 de 5
Após o Download do programa, é só instalar:
Depois de instalar o software, reinicie o computador e abra o MS Word. Uma nova aba aparecerá (clique em
Inline para inserir uma equação):
Agora, basta configurar o software como a seguir: (isso é necessário ser feito somente uma vez)


2 de 5
Uso do MathType
Onde devo usar o MathType?
Uma boa dica é: o que não estiver presente no teclado de seu computador deve ser inserido com esse software.
Exemplos:
Fórmulas e expressões matemáticas
b  b 2  4ac
,
2a
1
,
2
x  1 7 ,
x  2,5
32  9 ,
Letras gregas
 ,  ,  , ...
Números acompanhados de unidades de medida:
1 m2 , 2 cm3 , 5 °C
Alternativamente, nos casos anteriores, você pode usar o teclado do computador (COM RESSALVAS):
Você pode usar esses caracteres,
usando a tecla:
2 cm³
1 m²
Não use formatação sobrescrito para
produzir esses caracteres.
Símbolo de número ordinal
Exemplo: 1º e 2º lugares (fonte Arial)
1º e 2º lugares (fonte Calibri)
Veja que, dependendo da fonte, o
símbolo de ordinal por ter um risquinho.
Não confunda os dois símbolos.
Símbolo de grau
Exemplo: 5 C (fonte Arial)
5 C (fonte Calibri)
Não use formatação subscrito ou sobrescrito! Essa formatação pode ser perdida na diagramação.
Para não correr o risco de esquecimento das dicas anteriores, recomendamos o uso do MathType em todos os
casos.
Os objetos do MathType nos textos a seguir foram destacados para facilitar a visualização da forma correta e
da forma incorreta de utilizar o software.
ATENÇÃO: Não utilize ponto final (.) ou letra xis (x) para representar uma multiplicação. Esses caracteres
podem causar muita confusão dependendo da fonte utilizada para diagramar o texto.
Os caracteres corretos são o ponto centralizado (·) ou times (×).
3 de 5
Uso incorreto
Uso correto
O produto 2.3 (2x3) é igual a 6.
O produto 2  3 ( 2  3 ) é igual a 6.
O produto 2.3 ( 2 x 3 ) é igual a 6.
O produto 2  3 ( 2  3 ) é igual a 6.
Uso incorreto
Uso correto
23
6
(2x3)/6
(2*3)/6
Uso incorreto
Uso correto
Produto escalar: u . v = u1.v1 + u2.v2.
Produto escalar: u  v  u1v1  u2v 2
Lembrando que o produto escalar entre dois vetores Lembrando que o produto escalar entre dois vetores
é nulo, então:
é nulo, então:
n . AP = 0.
n  AP  0
(a, b, c). (x – x1, y – y1, z – z1) = 0
a, b,c    x – x1, y – y1, z – z1   0
a(x – x1) + b(y – y1) + c(z – z1) = 0
a  x – x1   b  y – y1   c  z – z1   0
ax – ax1 + by – by1 + cz – cz1 = 0
Sabendo que de acordo com a definição – by1 + cz –
ax – ax1  by – by1  cz – cz1  0
cz1 = d, chegamos à equação ax + by + cz + d = 0.
Sabendo
Denominada equação geral do plano.
– by1  cz – cz1  d ,
que
de
acordo
com
chegamos
a
à
definição
equação
ax  by  cz  d  0 . Denominada equação geral do
plano.
Dado o segmento PQ e o vetor gradiente f (x0, y0, Dado
o
segmento
PQ
e
o
vetor
gradiente
z0), determine a equação do plano tangente a
f  x0 , y 0 , z0  , determine a equação do plano
superfície.
tangente a superfície.
Resolução:
Resolução:
Sabemos que PQ = Q  P  (x – x0, y – y0, z – z0) e Sabemos que PQ  Q  P   x – x , y – y , z – z  e
0
0
0
 f f f 
, , .
 x y z 
f  
 f f f 
f   , ,  .
 x y z 
Fazendo o produto escalar entre os vetores temos:
Fazendo o produto escalar entre os vetores temos:
f ( x0, y0, z0). PQ = 0
f  x0 , y 0 , z0   PQ  0
 f f f 
 , ,  . (x – x0, y – y0, z – z0) = 0
 x y z 
 f f f 
 , ,    x – x0 , y – y 0 , z – z0   0
 x y z 
Obtendo a equação geral do plano tangente a uma Obtendo a equação geral do plano tangente a uma
superfície.
superfície.
 f 
 f 
  .( x – x0) +  y  .( y – y0) +
 x 
 
 f 
  .( z – z0) = 0
 z 
 f 
 f 
 f 
 x    x – x0    y    y – y 0    z    z – z0   0
 
 
 
Veja como obter genericamente a equação do plano Veja como obter genericamente a equação do plano
tangente.
4 de 5
tangente.
Tomamos um ponto P(x0, y0, z0) e Q( x, y , z ) , ambos Tomamos um ponto P  x0 , y 0 , z0  e Q( x, y , z ) , ambos
pertencentes à superfície. A fim de formar o vetor PQ
pertencentes à superfície. A fim de formar o vetor PQ
, e também um vetor gradiente a essa mesma , e também um vetor gradiente a essa mesma
superfície.
superfície.
Sabemos
que
PQ  Q  P   x  x 0 , y  y 0 , z  z 0 
 f f f 
e f  
,
,
 .
 x y z 
Sabemos que PQ  Q  P   x  x 0 , y  y 0 , z  z 0  e
 f f f 
f  
,
,
 .
 x y z 
Fazendo o produto escalar entre eles temos:
Fazendo o produto escalar entre eles temos:
f  x 0 , y 0 , z 0   PQ  0
f  x 0 , y 0 , z 0   PQ  0
 f f f 
,
,

   x  x 0, y  y 0, z  z 0   0
 x y z 
Obtendo a equação geral do plano tangente
 f f f 
,
,

   x  x 0, y  y 0, z  z 0   0
 x y z 
a uma superfície, no ponto  x 0 , y 0 , z 0  .
 f

 x

 f
  x  x0   

 y

 f
  y  y0   

 z

  z  z 0   0

Teorema de Fubini : Se f for contínua no retângulo


R   x , y  | a  x  b ,c  y  d ,então
bd
d b
R f  x , y  dA  a c f  x , y  dydx  c a f  x , y dxdy .
Sendo válida , quando f estiver contida na região ,
for descontinua em números finitos de
curvas e a int egral iterada exista .
Obtendo a equação geral do plano tangente a uma
superfície, no ponto  x0 , y 0 , z0  .
 f 
 f 
 f 

  x  x0   
  y  y0   
  z  z0   0
 x 
 y 
 z 
Teorema de Fubini: se f for contínua no retângulo
R   x, y  | a  x  b, c  y  d ,

f  x, y  dA 
R
b d

a c
f  x, y  dydx 
então
d b
  f  x, y  dxdy .
c a
Sendo válida, quando f estiver contida na região, for
descontínua em números finitos de curvas e a integral
iterada exista.
5 de 5