Notas da Aula 15 - Professores da UFF

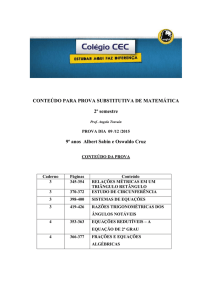
MÉTODOS NUM ÉRICOS PARA E QUAÇÕES DIFEREN CIAIS PARCIAIS
4- Método de Diferenças Finitas Aplicado
às Equações Diferenci ais Parciais.
4.1- Aproximação de Funções.
4.1.1- Aproximação por Polinômios.
4.1.2- Ajuste de Dados: M ínimos Quadrados.
4.2- Derivadas e Integrais Numéricas.
4.2.1- Aproximação de Derivadas por Dif erenças Finitas.
4.2.2- Aproximação de Integrais por Regras de Integração
Numérica.
4.3- Solução de Equações Diferenciais Ordinárias.
4.3.1- Problema de Val or Inicial.
4.3.2- Problema de Val or de Contorno.
4.4- Solução de Equações Diferenciais Parciais.
4.4- Solução de Equações Diferenciais Parciais.
Muitos problemas na ciência e na tecnologia podem ser
modelados por equações que estabelecem uma relação entre
funções desconhecidas u (o) e as derivadas destas fun ções ¶u (o.)
Equações deste tipo são chamadas Equações Diferenciais .
¶ (o)
Quando a função depende apenas de uma variável u (x) a
equação diferencial é chamada de Equação Diferencial
Ordinária, já que apenas podem aparecer as derivadas
k
d
u ( x) .
ordinárias da fun ção
dx k
Quando a função depende de mais de e uma vari ável u ( x1 , x2 ,L , xn )
a equação diferencial é chamada de Equação Diferencial
Parcial, já que podem
aparecer as di ferentes derivadas parciais
k
¶ u
desta função
(i, j = 1, L, n) e ( ki + L + k j = k ).
k
¶xiki L ¶x j j
4.4- Solução de Equações Diferenciais Parciais.
No tópico 4.3 estudamos Equações Diferenciais Ordin árias. No
tópico 4.4 estudaremos Equações Diferenciais Parciais .
Algumas Equações Diferenciais Parciais podem ser
classificadas como: Elípticas, Parabólicas e Hiperbólicas.
Faremos isto para uma Equação Diferencial Parcial Linear de
Segunda Ordem com duas vari áveis independentes:
¶ 2u
¶ 2u
¶ 2u
¶u
¶u
a
+b
+c
+d
+g
+ pu = f ( x, y )
¶x¶x
¶x¶y
¶y¶y
¶x
¶y
"( x, y ) Î W
A classificação depende do Sinal do Discriminante e os nomes
são por analogia com as se ções cônicas:
ì< 0 EDP Elíptica
ï
b2 - 4ací= 0 EDP Parabólica
ï> 0 EDP Hiperbólica
î
4.4- Solução de Equações Diferenciais Parciais.
Os três exemplos canônicos mais t ípicos são:
ìEquação de Poisson ü
¶ 2u
¶ 2u
+
= f ( x, y ) í
ý
EDP
Elíptica
¶x¶x ¶y¶y
î
þ
¶u
¶ 2u
=k
¶t
¶x¶x
2
¶ 2u
¶
u
= c2
¶t¶t
¶x¶x
ìEquação do Calor ü
í
ý
EDP
Parabólica
î
þ
æ
ö
ç
÷
2
2
¶
u
¶
u
ç Ñ 2 u = Ñ × Ñu =
÷
+
ç
¶x¶x ¶y¶y ÷
1
4
4
4
4
4
2
4
4444
3÷
ç
Laplaciano
è
ø
ìEquação da Onda ü
í
ý
EDP
Hiperbólic
a
î
þ
Estas EDP descrevem diferentes tipos de fenômenos que
requerem de diferentes técnicas para sua solu ção, tanto
analítica quanto num érica.
Nas três telas a seguir formalizamos EDP El íptica e Parab ólica
de 2 a Ordem e Hiperb ólica de 1 a Ordem.
4.4- Solução de Equações Diferenciais Parciais.
EDP Elíptica Linear de Segunda Ordem : L(u ) = f em W
n
¶2
¶
L = å Aij
+ å Bj
+ C , onde n é a dimensão do espaço.
¶xi ¶x j i =1 ¶xi
i , j =1
Os coeficientes constantes Aij , B j , C são reais. A matriz Aij é
simétrica. O operador L é dito ser elíptico se a matriz Aij é
n
[ ]
[ ]
definida positiva ou def inida negativa. Ou sej a, se
v T Av conserva o sinal "v Î R n
Num Problema de Val or de Contorno El íptico a solução deve
ser determinada impondo restri ções para a solu ção em todo o
contorno do dom ínio (Condições de Contorno ).
L(u ) = f em W
u (G) = u0 (Dirichlet)
Para este problema o M étodo de Di ferenças
Finitas transforma o PVC num si stema linear
esparço de equações algébricas.
4.4- Solução de Equações Diferenciais Parciais.
EDP Parab ólica Linear de Segunda Ordem : Se L é um
operador el íptico linear de segunda ordem com matriz [Aij ]
definida positiva, então a EDP a seguir é parabólica
¶u
= L(u ) - f em W e t > 0
(EDP)
¶t
u (G, t ) = u1 (Condição de Contorno de Dirichlet)
u (W, t 0 ) = u0 (Condição Inicial)
Num Problema de Val or de Contorno Parab ólico a solução
deve ser determinada i mpondo restri ções para a solu ção em
todo o contorno do dom ínio para cada instante de tempo
(Condições de Contorno ) e a Condição Inicial para todos os
pontos do interior do dom ínio.
4.4- Solução de Equações Diferenciais Parciais.
EDP Hiperb ólica Linear de Primeira Ordem : A EDP a seguir é
hiperbólica se a matriz A tem autovalores reais e pode ser
diagonalizada. Ou seja, se A tem um conjunto completo de
autovetores linearmente independentes.
¶u
¶u
=A
em W e t > 0
(EDP)
¶t
¶x
u (G+ , t ) = u1 (Condição de Contorno de Dirichlet)
u (W, t 0 ) = u0 (Condição Inicial)
Descreve o movimento de ondas e/ou transporte advectivo.
Num Problema de Val or de Contorno Hiperb ólico a solução
deve ser determinada i mpondo restri ções para a solu ção em
parte do contorno do dom ínio para cada instante de tempo
(Condições de Contorno ) e a Condição Inicial para todos os
pontos do interior do dom ínio.
4.4- Solução de Equações Diferenciais Parciais.
No que resta desta aula estudaremos apenas uma EDP Elíptica
Linear de Segunda Ordem. Para simplificar a exposição
estudaremos o caso quando temos duas variáveis
independentes e coef icientes constantes .
Logo nosso problema ser á descrito pela EDP:
¶ 2u
¶ 2u
¶ 2u
¶u
¶u
a
+b
+c
+d
+g
+ pu = f ( x, y )
¶x¶x
¶x¶y
¶y¶y
¶x
¶y
"( x, y ) Î W
b2 - 4ac < 0 . Se os
onde os coef icientes da EDP verif icam
coeficientes não são constantes a Condi ção de ELIPTICIDADE
deve ser verif icada para todos os pontos do dom ínio "( x, y ) Î W .
Para que o problema esteja bem posto devemos impor
restrições em todos os pontos do contorno do dom ínio.
4.4- Solução de Equações Diferenciais Parciais.
A EDP Elíptica Linear de Segunda Ordem com duas vari áveis
independentes e coef icientes constantes b2 - 4ac < 0 é:
¶ 2u
¶ 2u
¶ 2u
¶u
¶u
a
+b
+c
+d
+g
+ pu = f ( x, y )
¶x¶x
¶x¶y
¶y¶y
¶x
¶y
"( x, y ) Î W
Destacamos dois casos de restri ções impostas em todos os
pontos do contorno do dom ínio (Condições de Contorno - PVC).
Caso 1 {u ( x, y ) = uG
Caso 2
G = G1 È G 2
"( x, y ) Î G (CC de Dirichlet)
"( x, y ) Î G1 (CC de Dirichlet)
ìu ( x, y ) = uG1
ïr
"( x, y ) Î G 2 (CC de Neumann)
ín × Ñu = qG2
r
ï
onde
n
é o vetor normal ao contorno
î
4.4- Solução de Equações Diferenciais Parciais.
Problema 1 – Equação do Calor : Considere uma chapa f eita de
um material condutor de calor sujeita a alguma f onte externa de
calor e condi ções de contorno no contorno da chapa.
O fenômeno de condu ção do calor estacion ário nesta chapa
pode ser modelado pela seguinte equa ção:
Ñ× (-kÑu) = {
g (x)
14243
Difusão
"x ÎW (EDP)
Fonte Externa
Se o material é homogêneo, então k (x)não depende da posi ção
e a EDP se transforma em:
Exemplo 1 :
kÑ×Ñ
u= {
g (x)
1
4
24
3
2
"x ÎW =]0,1[´]0,1[ (EDP) ou k
Ñ
u= {
g (x)
123
Difusão
Fonte Externa
Caso 1
{u (x) = uG
Difusão
Fonte Externa
"x Î G (CC de Dirichlet)
Vamos aproximar o Laplaciano por f ormulas de Diferenças
Finitas Centradas :
4.4- Solução de Equações Diferenciais Parciais.
Note que o dom ínio agora é um quadrado uni tário e podemos
discretizar o problema construindo uma malha uniforme da
seguinte f orma:
(b - a )
xi = a + iDx, Dx =
,
i = 0,1,L , n
n
(d - c)
y j = c + jDy, Dy =
,
j = 0,1, L , m
m
Abaixo mostramos uma por ção (ESTENCIL-STENCIL) desta
malha:
4.4- Solução de Equações Diferenciais Parciais.
Denotemos por uij = u ( xi , y j ) a solu ção exata no n ó com
coordenadas ( xi , y j ) e seja U ij » u ( xi , y j )a sol ução aproximada.
Se aproximamos as deri vadas segunda pela formula de
Diferença Finita Centrada de segunda ordem:
¶ 2u( xi , y j )
¶x 2
¶ 2u( xi , y j )
¶y 2
u( xi + Dx, y j ) - 2u( xi , y j ) + u( xi - Dx, y j ) Ui +1, j - 2Uij + Ui -1, j
» D (u( xi , y j )) =
»
2
(Dx)
(Dx)2
2
u( xi , y j + Dy) - 2u( xi , y j ) + u( xi , y j - Dy) Ui, j +1 - 2Uij + Ui , j -1
» D (u( xi , y j )) =
»
2
(Dy)
(Dy)2
2
Então a aproxima ção pelo MDF para a EDP anterior consiste em
encontrar U ij » u ( xi , y j ) que satisfaz
éU i +1, j - 2U ij + U i -1, j U i , j +1 - 2U ij + U i , j -1 ù
- kê
+
ú = g ( xi , y j )
2
2
(Dx)
(Dy)
ë1444
24443 144424443û
¶ 2u
¶x 2
ì"0 < i < n
(EDP)
í
î"0 < j < m
¶ 2u
¶y 2
Por simplicidade consi deramos Dx = Dy º h e m = n logo
4.4- Solução de Equações Diferenciais Parciais.
[
]
k
- 2 U i -1, j + U i , j -1 - 4U i , j + U i +1, j + U i , j +1 = g ( xi , y j )
h
ì"0 < i < n
(EDP)
í
î"0 < j < n
Este esquema de di ferenças finitas pode ser representado
geometricamente pelo ESTENCIL de 5 pontos . Note que para
cada nó (ij) da malha temos uma inc ógnita U ij e uma equa ção
em diferenças (acima). Nas equa ções para os n ós perto do
contorno devem ser substitu ídas as condi ções de contorno,
semelhante ao caso unidimensional.
Como a malha tem n partição por x e n partição por y o número
total de inc ógnitas (graus de liberdade ) do sistema linear
equações será de (n-1)2 .
A ( n -1) 2 ´ ( n -1) 2 U = F
(M atriz Esparsa)
O Sistema para o Problema Unidimensional é de ordem n-1 e
para o Problema Bidimensional é de ordem (n-1)2. Logo, para o
Problema T ridimensional a ordem do sistema ser á (n-1)3.
4.4- Solução de Equações Diferenciais Parciais.
ì"0 < i < n
k
- 2 éëU i -1, j + U i , j -1 - 4U ij + Ui +1, j + U i , j +1 ùû = g ( xi , y j ) í
(EDP)
h
î"0 < j < n
k
- 2 [U 0,1 + U1,0 - 4U1,1 + U 2,1 + U1, 2 ] = g ( x1 , y1 ) {i = 1, j = 1
h
k
- 2 [U 0, 2 + U1,1 - 4U1,2 + U 2,2 + U1,3 ] = g ( x1 , y2 ) {i = 1, j = 2
h
LLLLLLLLLLLLLLLLLLLLLLLL
k
- 2 [U 0,n-1 + U1,n-2 - 4U1,n-1 + U 2,n-1 + U1,n ] = g ( x1 , yn-1 ) {i = 1, j = n - 1
h
k
- 2 [U1,1 + U 2,0 - 4U 2,1 + U 3,1 + U 2, 2 ] = g ( x2 , y1 ) {i = 2, j = 1
h
LLLLLLLLLLLLLLLLLLLLLLLL
n - 1 equações para i = 3,L, n - 1 equações para i = n - 1
k
- 2 [U n-2,n-1 + U n-1,n-2 - 4U n-1,n-1 + U n,n-1 + U n-1,n ] = g ( xn-1 , yn-1 ) {i = n - 1, j = n - 1
h
Note que a matriz é esparsa, ou seja, para cada linha apenas 5
4.4- Solução de Equações Diferenciais Parciais.
coeficientes são di ferentes de zero . Note também que temos
dois sub-índices para determinar a localiza ção de um n ó na
malha. Ou seja, temos ( n - 1) 2 inc ógnitas:
{U
11
,
,U1,2 ,L,U1,n-1} , {U 2,1,U 2,2 ,L,U 2,n-1} ,L, {U n-11, ,U n-1,2 ,L,U n-1,n-1}
2 sub-índices i = 1,L,(n - 1) e j = 1,L,(n - 1)
{U ,U ,L,U }{, U
{U
,U
1
2
( n - 2)( n -1) +1
( n -1)
( n-1) +1
( n- 2)( n -1) + 2
,U ( n-1)+ 2 ,L,U ( n-1) +( n-1) },L,
,L,U ( n-2)(n-1)+( n-1) } 1 sub - índice m = 1,L, (n - 1)(n - 1)
Isto quer dizer que apenas precisamos de 1 sub-índice para
determinar a localiza ção do nó na malha. Ou seja, que devemos
construir uma função que faça uma ligação entre os dois sub índices e a numera ção global (1 sub-índice). Destacamos que
esta função vai determinar a estrutura da matri z do sistema
linear de equa ções algébricas.
Existem diferentes maneiras de construir a função de ligação.
Uma forma muito simples é reordenar a numera ção por linhas.
4.4- Solução de Equações Diferenciais Parciais.
Neste caso a função de ligação com varredura interna em i e
externa em j é:
m(i, j ) = ( j - 1)( n - 1) + i, com i = 1, L, (n - 1) para cada j = 1,L , ( n - 1)
A matriz A ( n -1) 2 ´ ( n -1) 2 seria f ormada por matri zes blocos d e
ordem (n-1) na forma:
éT I
ù
êI T I
ú
ê
ú
ú
I T I
-k ê
A= 2 ê
ú
O O O ú
h ê
ê
I T Iú
ê
ú
I
T
ë
û
é-4 1
ù
ê 1 -4 1
ú
ê
ú
ê
ú
1 -4 1
T(n-1),(n-1) = ê
ú
O
O
O
ê
ú
ê
1 -4 1 ú
ê
ú
1
4
ë
û
A matriz I é a matriz identidade.
Se reordenamos a numera ção por coluna a função de ligação
seria:
m(i, j ) = (i - 1)( n - 1) + j , com j = 1,L , (n - 1) para cada i = 1, L, (n - 1)
4.4- Solução de Equações Diferenciais Parciais.
Precisão e Estabilidade : Semelhante ao caso 1D U ij » u ( xi , y j )
Erro da Solu ção Aproximada?
1- Erro em cada ponto ( xi , y j ):
e( xi , y j ) = U ij - u ( xi , y j )
2- Erro Global : E G = U - u , com U =[U1,L,U 2 ]T e u =[u1,L,u 2 ]T
(n-1)
(n-1)
-kÑ×Ñu = g(x) "x ÎWü
ý (1) Aplicando o MDF Þ A(n-1)2´(n-1)2 U = F
u(G) = uG ,
þ
(2)
3- Note que em geral u não satisf az (2) e isto def ine o chamado
Erro Local
E L = A ( n-1)2 ´( n -1)2 u - F Þ A ( n-1)2 ´( n -1)2 u = F + E L
(3)
A componente i do erro local (linha i) é
( E L )i
-k
= 2 [ui -1, j + ui +1, j - 4uij + ui , j -1 + ui , j +1 ] - gij "0 < i, j < n (EDP)
h
4.4- Solução de Equações Diferenciais Parciais.
Se a solução exata do problema é suave expandindo ela em
serie de T aylor entorno do ponto ( xi , y j ). Substituindo na equa ção
anterior esta expansão e a EDP obtemos:
( E L )i
é 1 2 æ ¶ 4u( xi , y j ) ¶ 4u( xi , y j ) ö
ù
4
= -k ê h ç
+
÷÷ + O(h ) ú "0 < i, j < n (EDP)
4
4
ç
¶x
¶y
êë12 è
úû
ø
Ou seja, o erro local é de ordem 2 ( EL )i = Ci h2
Podemos estabelecer uma rela ção entre o Erro Local EL e o
Erro Global EG . Para isto fa ça a diferença entre (2)-(3) e
obtemos: A 2 2 (U - u) = -EL ou A 2 2 EG = -EL
( n-1) ´( n-1) 123
( n-1) ´( n-1)
EG
Note que este é o mesmo sistema de equa ções em diferenças
obtido para U exceto que em lugar de Ftemos - EL. Para
alguma norma o Erro Global é da mesma ordem que o Local,
indicando que nesta norma o sistema pode ser est ável
-1
h
( A ) < C para h suficientemente pequeno Þ EGh £ C EhL = C O(h2 )
Frase do Dia
“Although to penetrate i nto the intimate
mysteries of nature and thence to l earn the
true causes of phenomena i s not allowed to
us, nevertheless it can happen that a certai n
fictive hypothes is may suffice for explaining
many phenomena. ”
Leonhard Euler (A mesma das Aula 9, 11, 12,13)
“... the study of Euler’s works will remain the
best for different fields of mathemati cs and
nothing else can replace it.”
Friedrich Gauss