Ressonância Eletromagnética Quântica e Clássica

Ressonância Eletromagnética Quântica e Clássica
D. Gioielli, R. Voivodic, V. Fernandes
1
algum parâmtro do sistema. Ou seja, em regime
de ressonância, fornece-se ao sistema energia
suficiente para que esse altere o sentido de seu
spin, esse efeito de troca no sentido do spin será
abordado em mais detalhes.
Resumo
Ressonância é um fenômeno vastamente
estudado em física clássica para diversos
sistemas oscilantes. Este experimento teve como
objetivo o estudo de fenômenos de ressonância
em nível quântico e sua comparação com
sistemas ressonantes clássicos. Para tanto foi
estudada a ressonância magnética nuclear
(RMN) e a ressonância paramagnética eletrônica
(ESR).
No estudo do ESR foi medido o campo
magnético necessário para se obter um sinal de
ressonância da amostra de DPPH para diversos
valores de frequência, a partir destes dados foi
possível calcular o fator giroscópico característico
(2,035±0,019).
Para o estudo do RMN foi realizado um
procedimento similar (para amostras de água,
glicerina, poliestireno e teflon),a partir dos quais
foram
calculados
os
fatoresgiroscópicos
característicos do Hidrogênio (5,62±0,16) e do
Flúor (5,06±0,11).
2
2.1
2.3
Spin é uma característica intrínseca de
partículas
elementares,
e
também
a
manifestação
dessas
características
em
partículas maiores, compostas por partículas
elementares, como por exemplo prótons e
nêutrons(que são sabidamente compostos por
quarks, segundo a teoria da física quântica).
Fisicamente essa característica intrínseca das
partículas, denominada spin, é um momento
magnético intrínseco. Por esse motivo ele
interage com campos magnéticos.
Instrumentalmente o Spin é quarto número
quântico que define uma partícula, e esse
número é sempre inteiro ou uma fração.
2.4 Momento magnético paramagnético e
nuclear
Introdução
O
momento
paramagnéticoé
uma
característica macroscópica da matéria que se dá
pela
soma
dos
spins
dos
elétrons
desemparelhados na última camada dos átomos.
Os elétrons das camadas eletrônicas dos átomos
tem spin igual a ½, sendo assim podem assumir,
segunda a teoria quântica, dois estados
degenerados (que tem a mesma energia) ½ ou ½. Elétrons emparelhados em um mesmo orbital
tem os spins complementares, e por isso a soma
dos spins se anula e não acarreta nenhum
fenômeno macroscópico, porém há átomos que
tem um elétron desemparelhado na última
camada eletrônica, esses átomos constituem os
elementos paramagnéticos. A soma dos spins
desemparelhados dos elétrons das substâncias
paramagnéticas faz com que elas tenham um
momento magnético total resultante.
O momento magnético nuclear, por sua vez,
diferentemente do momento paramagnético
eletrônico, já é diretamente proveniente do spin
nuclear, não necessitando de nenhum explicação
teórica a mais.
Ressonância
Ressonância é um termo genérico, designado
para descrever um regime particular de um
sistema oscilatório, onde há uma faixa de
frequências de oscilações, chamadas frequências
de ressonância, nas quais o sistema oscila com
amplitude máxima.
Em física clássica essa descrição para
ressonância é completa, porém ao pretender-se
também englobar os fenômenos da física
quântica, deve se permitir alterar alguns aspectos
do conceito.
2.2
Spin
A ressonância e a Física Quântica
A ressonância pode se dar em sistemas
descritos pelas teorias da física quântica, é o
caso da maior parte do experimento em questão.
Nesse experimento estudamos elementos da
ressonância magnética eletrônica e nuclear. Em
ambos os casos, o regime de ressonância se
caracteriza pela troca do sentido da orientação
do spin, ao invés de por amplitudes máximas em
1
2.5
Como, tanto k quanto
valem ½ ou -½, o
diferença de energias valem:
Efeito Zeeman
À temperatura ambiente esses momentos
magnéticos são dispersos pela agitação térmica,
ou seja, não estão orientados em nenhuma
direção específica. Quando submetido porém a
um campo
externo, os momentos magnéticos
individuais de cada átomo sofrem um torque
dado pela expressão:
ESR:
(3)
Bohr:
(7)
Frequência de Larmor
Temos um regime portanto onde momentos
magnéticos são submetidos a um campo externo,
e ficam alinhados com o campo, porém é uma
propriedade quântica que esses momentos
magnéticos não ficam completamente alinhados
com o campo, há portanto um ângulo do
momento magnético com o campo externo, e ao
redor desse campo há uma precessão do
momento magnético, conforme mostrado na
imagem que se segue:
Figura 1 - Precessão de larmor de um momento
[2]
magnético em volta de um campo magnético externo.
Onde g é um fator giroscópico característico
de cada núcleo,
é um fator giroscópico
característico de cada átomo paramagnético, e
sãorespectivamente o magneton nuclear e o
magneton de Bohr, k é o número quântico do
spin do núcleo, valendo ½ ou -½, e
é o
número quântico do spin do elétron, valendo
também ½ ou -½.
Os magnetons, nuclear os de Bohr, são
constantes que relacionam o momento magnético
ao
momento
angular
total,
e
valem
respectivamente:
Nuclear:
ESR:
2.6
E esse torque alinha os momentos de
maneira que eles passam a estar alinhados com
a direção do campo magnético externo , porém
seu sentido, ou sua orientação, pode ser paralela
ou antiparalela à do campo. A orientação paralela
encontra-se num estado de menos energia do
que a orientação antiparalela.
Assim
sendo,
quando
os
momentos
magnéticos, seja dos núcleos, seja dos elétrons,
são alinhados pelo campo magnética externo,
eles não estão mais em estados degenerados em
energia, ou seja, perdem a igualdade em sua
energia.
A energia de um momento magnético no
campo
é dada por diferentes expressões para
a ressonância magnética nuclear (RMN) e para a
ressonância paramagnética eletrônica (ESR)a
seguir temos ambas:
(2)
(6)
Essa diferença de energia entre os dois
estados do spin da partícula é denominada efeito
Zeeman.
(1)
RMN:
RMN:
Essa precessão é denominado precessão de
Larmor, e tem uma frequência característica
chamada frequência de Larmor. Essa frequência
depende da magnitude do campo magnético
externo e também do material em questão,
conforme a seguinte expressão:
(8)
Essa frequência caracteriza portanto o fator
giromagnético g do material.
2.7 Ressonância Quântica com inversão de
spin
(4)
Para colocar o sistema descrito até agora em
estado de ressonância, devemos sumetê-lo a um
campo magnético variável secundário
, que
seja perpendicular à
, e que tenha a
(5)
2
especificidade devariar com a frequência de
larmor apresentada anteriormente, que é também
a frequência do fóton de energia igual à diferença
de energia
gerada pelo efeito Zeeman.
Ao configurar os parâmetros de seu sistema
para que as frequências de Larmor e do fóton
gerada pelo campo
sejam as mesmas, o
sistema recebe precisamente a quantidade de
energia que necessita para que um spin com
orientação paralela (de menor energia), mude
sua
orientação
para
paralela
(absorvendaprecisamente a quantidade de
energia ). Fazendo com que o sistema absorva
a energia do campo , de maneira semelhante a
um sistema clássico que entra em ressonância.
2.8
No primeiro dia o objetivo era determinar o
fator g do DPPH (1-diphenyl-2-picryl-hidrazyl) e
em seguida medir o análogo clássico utilizando
um circuito passivo (basicamente um circuito
RLC). Já no segundo o objetivo era determinar o
fator g para diversas amostras.
Em ambas as experiencias utilizou-se um
campo uniforme com modulação (com um
pequeno campo oscilante em torno do campo
principal com a frequência da rede) para orientar
o spin das partículas de interesse, um campo
variável com frequência controlada perpendicular
ao uniforme modulado utilizado para se encontrar
a frequência de ressonância. Em ambos foi
utilizado um osciloscópio no modo XY para
realizar as medidas e encontrar-se a
ressonância, e um multímetro para medidas
complementares da corrente, e no segundo dia
foi também utilizado um medidor de campo
magnético.
No primeiro dia, o campo magnético uniforme
com modulação foi criado por bobinas de
Helmholtz (de até 4mT), e o campo oscilante
perpendicular por solenoide (na verdade haviam
três tamanhos disponíveis que possuíam um
certo range de frequências). O DPPH era então
colocado dentro desse solenoide e a frequência
de
ressonância
procurada,
utilizando
o
osciloscópio, para cada valor do campo das
bobinas de Helmholtz (Figura 2). A corrente que
passava tanto pela bobina de Helmholtz quanto
pelo solenoide era gerada por um mesmo
gerador, onde era possível ajustar a frequência
dos solenoides.
Ressonância no sistema RLC
A parte clássica do experimento corresponde
à observação da ressonância eletromagnética em
um circuito RLC. O circuito RLC obedece a
equação
A frequência natural é igual ao inverso da raiz
quadrada do produto da indutância pela
capacitância, conforme a equação a seguir:
(9)
3
Arranjo experimental
O experimento foi basicamente dividido em
dois dias de medições, no primeiro dia o grupo
utilizou dois equipamentos diferentes (figuras 2 e
3) e no segundo um outro (figura 4).
Figura 2 - Representação do arranjo experimental utilizado na primeira experiência do primeiro dia, já com o gerador das
correntes (equipamento central) e osciloscópio.
Ainda no primeiro dia, para se verificar o
fenômeno de ressonância de uma forma
“clássica”, foi utilizado um outro arranjo, onde
agora ao invés da ressonância ser criada pelos
spins das partículas, era criada apenas por um
circuito RLC. Para isso substituiu-se as bobinas
3
de Helmholtz e a amostra por outra bobina ligada
ao capacitor (de capacitância ajustável), de forma
que no circuito apresentam-se componentes
indutores (bobinas), capacitores (capacitores) e
resistores (própria resistência intrínseca do
circuito) onde a frequência de ressonância
(frequência natural) podia ser ajustada mudandose a capacitância do circuito, conforme a
equação 9. Novamente, para cada capacitância,
foi procurada a frequência de ressonância
utilizando-se osciloscópio. As correntes do
circuito foram geradas pelo mesmo gerador do
primeiro arranjo.
Note que nesse caso, a capacitância exerce o
papel do campo magnético gerado pelas bobinas
de Helmholtz, pois agora é ela que muda a
frequência natural do sistema.
modulação e a frequência do campo oscilante
perpendicular, e para cada uma dessas
frequências foi procurada a ressonância do
sistema utilizando-se o osciloscópio. Uma vez
encontrada a ressonância era utilizado o medidor
de campo magnético para se saber (diretamente
dessa vez) o campo as bobinas maiores, pois
possíveis determinações teóricas desse campo
baseado na corrente passando nas bobinas
poderia ser falha (pelo menos em aproximações
usuais) pelo fato de a barra de ferro poder ser
magnetizada pelo campo intenso e afetar o valor
calculado.
Efetivamente os experimentos de ambos os
dias possuem os mesmos objetivos e arranjos
experimentais iguais, levemente alterados pela
necessidade de campo mais intenso no segundo
dia por conta da maior dificuldade na medição da
ressonância do próton.
Figura 4 - Representação de NMR, com o gerador das
correntes e osciloscópio. O bloco à direita possui as duas
bobinas geradoras do campo intenso ligadas pela barra de
ferro com a cavidade onde está o campo oscilante
perpendicular e a amostra.
Figura 3 - Representação do arranjo experimental
utilizado na experiência de ressonância clássica, já com o
gerador das correntes e osciloscópio. Agora o capacitor
acoplado à bobina faz o papel do campo magnético do
primeiro arranjo, regula o valor da frequência.
4
No segundo dia foi utilizado um arranjo com
objetivos muito parecidos com o do primeiro,
porém dessa vez, por conta da ordem de
grandeza das energias envolvidas, foi necessário
utilizar-se um arranjo experimental um pouco
diferente.
Para criar o campo magnético uniforme com
modulação foram utilizadas bobinas mais
potentes ligadas por um pedaço de metal, que
tinha o papel de guiar o campo magnético até a
amostra, que criava um campo magnético de até
0.5T. O campo oscilante perpendicular era criada
por uma pequena cavidade onde havia uma
bobina menor. As amostras de glicerina, água,
poliestireno ou teflon eram então colocadas na
cavidade da barra de ferro entre as duas bobinas
maiores, e novamente as correntes do sistema
eram geradas por um gerador onde era possível
ajustar o módulo do campo mais forte com
4.1
Análise de Dados e conclusões
Ressonância Magnética Nuclear
A partir dos dados para cada um dos quatro
materiais utilizados foi possível encontrar a curva
de ressonância característica para cada um dos
materiais, Figura 5.
4
Energia (J)
Tabela 3 – fatores giroscópicos da
literatura e teste Z
Fator
Teste Z
Giroscópico
Hidrogênio
5,59
0,23
Flúor
5,26
1,79
1,05E-26
0,35 0,375 0,4 0,425 0,45 0,475 0,5
4.2
Campo magnético (T)
Glicerina
Teflon
Poliestireno
Ressonância paramagnéticaEletrônico
A partir das medidas foi possível calcular a
energia dos fótons absorvidos em função do
campo magnético aplicado à amostra.
Tabela 4 - Energias absorvidas em
função do campo magnético.
Campo Magnético (mT)
Energia
(J)
0,55
9,94E-27
0,69
1,33E-26
0,86
1,65E-26
1,07
1,99E-26
1,24
2,33E-26
1,41
2,65E-26
1,57
2,98E-26
1,76
3,33E-26
1,96
3,65E-26
2,11
3,96E-26
2,29
4,31E-26
2,46
4,64E-26
2,63
4,96E-26
2,78
5,29E-26
2,96
5,65E-26
3,16
6,00E-26
3,32
6,28E-26
3,53
6,64E-26
3,70
6,97E-26
3,88
7,30E-26
4,03
7,62E-26
4,23
7,96E-26
4,40
8,28E-26
A tabela acima mostra os valores calculados a
partir dos quais foi possível fazer um ajuste de
reta segundo o modelo proposto pelas equações
(5) e (7).
Água
Figura 5 - Gráfico da Energia absorvida pelo sistema em
função do campo magnético principal ao qual as amostras
foram submetidas.
Cada curva foi ajustada por uma reta a partir
do Método de Mínimos Quadrados, seguindo
como modelos aa equaçõles (4) e (6), foi possível
calcular o fator giroscópico para cada material,
apresentados na tabela que se segue.
Tabela 1 – Fatores giroscópicos das
amostras
Fator Giroscópico
Água
5,55 ±0,12
Glicerina
5,64 ±0,14
Poliestireno
5,68 ±0,14
Teflon
5,06 ±0,11
Como podemos ver, o valor do fator
giroscópico da água, glicerina e poliestireno são
compatíveis entre si como era de se esperar,
uma vez que era esperado visualizar o sinal de
ressonância gerado pelo núcleo do hidrogênio.
Para o Teflon, obtemos um fator giroscópico
diferente, já que neste caso estamos observando
a ressonância do núcleo do flúor.
Tabela 2 – Fatores giroscópicos
nucleares
Fator Giroscópico
Hidrogênio
5,62 ±0,16
Flúor
5,06 ±0,11
Depois de obter fator giroscópico para os
núcleos do Hidrogênio e Flúor, esses valores
foram comparados com os valores teóricos
encontrados na literatura.
5
principal, para diferentes valores de capacitância, e sem
nenhum circuito ressonante sendo induzido.
Energia (J)
5
No estudo da Ressonância Magnética Nuclear
foi possível observar que o modelo proposto nas
equações (4) e (6) descrevem bem o fenômeno
físico estudado, de modo que foi possível
encontrar os fatores giroscópicoscaracterísticos
do Hidrogênio (5,62±0,16) e do Flúor (5,06±0,11)
com uma precisão razoável em relação ao valor
teórico, fator Z<1 para o Hidrogênio e fator Z<2
para o Flúor.
No estudo da RessonênciaParamagnética
Eletrônica foi possível obter uma valor para o
fator giroscópico característico (2,035±0,019)
compatível com o valor teórico esperado (fator
Z<2), embora o grupo tenha tido dificuldades
durante as medições devido a problemas de mal
contato em uma das bobinas de radio-frequência
utilizadas no experimento.
Por fim a realização do experimento utilizando
o circuito passivo RLC teve um papel
fundamental na compreensão do fenômeno
observado ao fazer a ligação entre o fenômeno
quântico e o conhecimento clássico sobre
ressonância.
5,00E-27
0,25
2,25
4,25
Campo Magnético (mT)
Figura 6 – Gráfico da energia absorvida pelo sistema em
função do campo magnético aplicado à amostra.
Feito o ajuste, foi possível calcular o fator
giroscópico para o elétron do DPPH, o resultado
será apresentado na tabela abaixo em conjunto
com o valor teórico encontrado na literatura e o
resultado do teste Z.
Tabela 5 – Fator giroscópico calculado,
teorico, e teste Z, para o DPPH
Fator giroscópico
2,035 ±0,019
Calculado
Fator giroscópico
2,004
Teórico
Teste Z
1,68
6
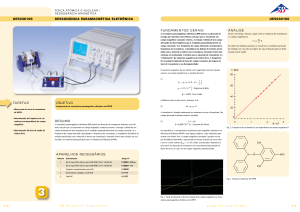
4.3 Ressonância de absorção de um
circuito oscilador RF passivo
20
10
Corrente (mA)
Tensão (mV)
[2] Wikipédia, Imagem por ressonância
magnética, acessado em 23 de Junho de 2014,
em
<http://pt.wikipedia.org/wiki/Resson%C3%A2ncia
_magn%C3%A9tica#Intera.C3.A7.C3.A3o_Zeem
an>
40
30
[3] Wikipédia, Nuclear magnetic ressonance,
acessado em 23 de Junho de 2014, em
<http://en.wikipedia.org/wiki/Nuclear_magnetic_re
sonance#Magnetic_resonance_by_nuclei>
0
21
26
31
Referências
[1] Wikipédia, Espectroscopia de ressonância
eletrônica, acessado em 23 de Junho de 2014,
em
<http://pt.wikipedia.org/wiki/Espectroscopia_de_r
esson%C3%A2ncia_paramagn%C3%A9tica_elec
tr%C3%B3nica>
A partir dos dados medidos foi possível fazer a
verificação do efeito de ressonância para um
circuito RLC. O gráfico abaixo mostra as curvas
obtidas para a corrente e a tensão para três
valores diferentes de capacitância em função da
frequência.
1600
1400
1200
1000
800
600
400
200
0
Conclusão
36
Frequência (MHz)
[4] Wikipédia, Momento mgnético, acessado
em
23
de
Junho
de
2014,
em
<http://pt.wikipedia.org/wiki/Momento_magn%C3
%A9tico>
Figura 7 – Gráfico da tensão e da corrente observadas
no sistema em função da frequência do campo magnético
6
[5] Wikipédia, Spin, acessado em 23 de Junho
de 2014, em <http://pt.wikipedia.org/wiki/Spin>
[6] Wikipédia, Larmos precession, acessado
em
23
de
Junho
de
2014,
em
<http://en.wikipedia.org/wiki/Larmor_precession>
[7] Wikipédia, Magnetom de Bohr, acessado
em
23
de
Junho
de
2014,
em
<http://pt.wikipedia.org/wiki/Magnet%C3%A3o_de
_Bohr>
7