caderno_01_matematica (1) - Diretoria de Ensino

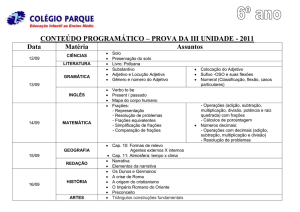
Diretoria de Ensino – Região de Bragança Paulista
N°01
Cadernos do Núcleo Pedagógico
Matemática
Números Racionais
Bragança Paulista
Junho, 2016
GOVERNO DO ESTADO DE SÃO PAULO
Geraldo Alckmin
Governador
Márcio França
Vice-Governador
José Renato Nalini
Secretario da Educação
Salim Andraus Junior
Dirigente Regional
David Fachim Martignago
Diretor do Núcleo Pedagógico
Maria Edite de Camargo Dmitrasinovic
PCNP de Matemática
Samara Valdo de Oliveira
PCNP de Matemática
Bragança Paulista
Junho, 2016
2
Sumário
1.
Introdução ...................................................................................................................3
Orientações Técnicas já realizadas contemplando o assunto: ............................................6
2.
Localização no Currículo Oficial do Estado de São Paulo ................................................7
2.1. ENSINO FUNDAMENTAL – ANOS FINAIS .....................................................................7
2.2. ENSINO MÉDIO..........................................................................................................8
3. Localização de habilidades referentes nas Avaliações de Aprendizagem em Processo ........9
AAP – 2011 ......................................................................................................................9
AAP -2012 ........................................................................................................................9
AAP -2013 ........................................................................................................................9
AAP -2014 ...................................................................................................................... 10
AAP -2015 ...................................................................................................................... 11
AAP -2016 ...................................................................................................................... 12
4. Aulas diversificadas........................................................................................................ 13
4.1 Reconhecer a porcentagem como representação da fração ....................................... 13
4.2 Jogo da Memória de Números Racionais ................................................................... 16
4.3 Jogo Papa Todas ....................................................................................................... 16
4.3 - Jogo do Pare de Frações.......................................................................................... 18
5. Banco de dados.............................................................................................................. 21
6. Bibliografia .................................................................................................................... 33
2
1. Introdução
Ensinar matemática é importante porque ela está presente em tudo o que nos
rodeia, com maior ou menor complexidade. Perceber isso é compreender o mundo
em nossa volta e poder atuar nele como cidadão, em casa, na rua, nas várias
profissões, na cidade, no campo, nas várias culturas o ser humano necessita da
matemática.
Devemos compreender a Matemática como uma disciplina de investigação e não de
conteúdo pronto e acabado. Ela é um espaço de ação e criatividade. A Matemática
que deve ser ensinada e estudada, de alguma forma, deve ser útil para os alunos,
ajudando-os na compreensão, explicação ou organização da realidade e
possibilitando, desta forma, que os alunos tenham condições de refletir sobre o seu
fazer
para
construir
o
saber.
Para isso, é necessário que ensino da disciplina exija do professor que ele não saiba
apenas o que ensinar, mas também a quem ensinar e como ensinar, levando em
consideração as diferenças e especificidades de cada turma.
Esse caderno justifica-se pela importância de ser um instrumento de apoio
didático e pedagógico para suprir dificuldades de aprendizagem relacionada a
Matemática.
Trata-se de oportunizar o professor situações de ensino aprendizagem voltadas
a cada dificuldade específica.
Números Racionais
O ensino de Números Racionais que compreende desde a numeração decimal,
as frações, as dízimas periódicas, as porcentagens, dentre outros, proporciona ao aluno
melhor compreensão e atuação no mundo cotidiano. Ao reconhecer e resolver
problemas que envolvam números racionais, o aluno consegue consequentemente
analisar situações que estão relacionadas no seu dia-a-dia, pois os mesmos se
encontram em grande parte da nossa vida, seja ela escolar ou não. Podemos encontrar
os Números Racionais, tanto em situações caseiras: receitas, uso de material de limpeza
e higiene, dentre outros, em jornais e revistas com apresentação para análise de dados
nas reportagens ou em gráficos e tabelas. Em problemas escolares relacionados a vários
outros conteúdos. Enfim, a utilização dos Números Racionais é muito vasta.
Hoje em dia é comum o uso de frações. Houve tempo, porém que as mesmas não eram
conhecidas. O homem a introduziu quando começou a medir e representar medidas. Os
egípcios usavam apenas frações que possuíam o número 1 dividido por um número
inteiro, como por exemplo: 1/2, 1/3, 1/4 ,1/5. Tais frações eram denominadas frações
egípcias e ainda hoje têm muitas aplicações práticas. Outras frações foram descobertas
pelos mesmos povos, as quais eram expressas em termos de frações egípcias, como:
1/2+1/3 = 1/6. Os babilônios usavam geralmente frações com denominador 60. É
provável que o uso desse denominador se deva ao fato que é um número menor do que
100 com maior quantidade de divisores inteiros. Os romanos, por sua vez, usavam
constantemente frações com denominador 12. Provavelmente, eles assim o faziam por
3
ser um número que embora pequeno, possui um número expressivo de divisores
inteiros. Com o passar dos tempos, muitas notações foram usadas para representar
frações. A atual maneira de representação data do século XVI. Os números decimais têm
origem nas frações decimais. Por exemplo, a fração 1/2 equivale à fração 5/10 que
equivale ao número decimal 0,5.
Os números decimais simplificaram muito os cálculos e passaram a ser usados com mais
ênfase após a criação do sistema métrico decimal.
“Graças à descoberta das frações denominadas ‘decimais’ (aquela cujo denominador é
uma potência de 10), foi pouco a pouco transparecendo o interesse em prolongar a
numeração decimal de posição no outro sentido, isto é, em termos modernos, na
representação dos números ‘depois da vírgula’. O que permitiu a notação sem nenhuma
dificuldade de todas as frações, além de mostrar nitidamente os inteiros como frações
particulares: aquelas cuja representação não comporta nenhum algarismo depois da
vírgula”. (IFRAH, 1987).
Um Número Racional se apresenta como fração, que pode ser escrito na forma a/b,
onde a e b são números inteiros e b ≠ 0 . Podemos assim representar o Conjunto dos
Números Racionais:
𝒂
{ / 𝐚, 𝐛 ∈ ℤ, 𝒃 ≠ 𝟎 }
𝒃
Esse número fracionário pode também ser representado como número decimal em
que, ao dividirmos o numerador a pelo denominador b, obteremos um número com
vírgula que exige um processo a ser realizado para se chegar a esse valor. Caso esse
número decimal seja infinito e venham repetidos valores com uma sequencia
determinada, determinamos esse número decimal de dízima periódica, que por sua vez
pode ser simples (quando é formada apenas pelo período após a vírgula) ou composta
(se possui uma parte que não se repete entre a parte inteira e o período). Caso a divisão
dessa fração seja um número decimal infinito e não periódico, o chamaremos de
número irracional (outro conjunto de números, que não será neste artigo estudado).
Podemos também encontrar a fração geratriz da dízima periódica, se ao invés de fração
tivermos apenas a dízima periódica. Além dessas formas e outras ainda não citadas, os
Números Racionais podem ser usados em cálculos matemáticos e admitem a adição,
subtração, multiplicação, divisão, potenciação, radiciação, módulo, simétrico, entre
outros e suas propriedades, os quais podem estar relacionados como equações, médias
e etc. Segundo Kieren (Apud Mendes, 2004) há sete subconstructos para os números
racionais e desde o início da escolarização é passado para o aluno somente a ideia de
medida fracionária (relação parte-todo). Somente após alguns anos de estudos é que os
alunos passam a ter noção de outros subconstrutos como razão, decimal do número
racional e outros. Os subconstructos vistos pelo autor são relações que um número
racional pode ter:
4
1. Medida fracionária (relação parte-todo): quantidades contínuas e discretas, base
fundamental para a construção do conceito de número racional e introduzido ao aluno
desde seu primeiro contato com frações.
2. Coordenada linear: Enfatiza a questão intervalar, a densidade e a descontinuidade;
os números racionais são interpretados como pontos sobre uma reta numérica.
3. Quociente: Representação de uma divisão a: b, na forma a/b, ou seja, a dividido por
b, b ≠ 0. 4. Razão: Relação expressa entre duas quantidades de uma mesma espécie.
5. Taxa de número racional: Aquele que define uma nova quantidade como uma relação
entre duas outras quantidades; a velocidade é um exemplo de taxa.
6. Decimal do número racional: Enfatiza as propriedades do número racional, na sua
representação decimal, associadas ao sistema de numeração decimal.
7. Operador: Relacionado à ideia de função, como uma transformação. Trata-se da
noção amplia-encolhe. Esse subscontruto impõe ao número racional p/q uma
interpretação algébrica, significando uma função que, quando aplicada em figuras
geométricas, transforma-as em figuras semelhantes, quando aplicadas a um conjunto
discreto atua como multiplicador-divisor. Podem ser observados alguns exemplos de
cada subconstruto no sentido de exemplificar melhor o significado deles.
1º) O subconstruto Medida fracionária (relação parte-todo) é usado geralmente desde
as séries iniciais do Ensino Fundamental quando é passada para o aluno a noção de
frações de um inteiro. Como exemplos podem-se observar:
a) 3/4 de uma barra de chocolate;
b) 5/8 de uma pizza;
2º) Para Coordenada Linear é passada ao aluno a ideia de reta numérica dos números
racionais a partir da 6ª Ano do Ensino Fundamental, onde os alunos começam a
demarcar números em pontos da reta.
a) A representação do número 3/2 na reta numérica;
b) A representação do número 4/5 na reta numérica.
3º) O subconstruto quociente é trabalhado no Ensino Fundamental desde a 3ª série,
mas recebe uma consolidação maior na 5ª e 6ª Anos no ensino de frações ao se
transformar uma fração em número decimal.
a) Transformação de 3/4 em número decimal;
b) Resolução de equações do tipo 3.x =12.
4º) Ao se estudar os conteúdos envolvendo razões e proporções geralmente ministrados
na 6ª Ano, observa-se o subconstruto razão onde podemos observar, por exemplo, o
conceito de escalas.
5º) O subconstruto taxa de número racional é estudado pelo Ensino Fundamental
apenas na último Ano (9º), onde são passadas algumas ideias de velocidade ou
aceleração, por exemplo.
6º) Para o subconstruto decimal do número racional pode ser observado, como
exemplo, a transformação de frações em números decimais e vice-versa, vista desde a
5º Ano do Ensino Fundamental.
5
7º) Operador é um subconstruto muito trabalhado em geometria em ampliações e
reduções de figuras semelhantes e em relações utilizadas em funções, podendo ser
observado mais nas últimas séries do Ensino Fundamental.
a) Preço do pão em uma padaria: P(x) = 0,25x , onde x é a quantidade de pães a ser
comprada e P(x) é o valor a ser pago pelos pães.
ENSINO E APRENDIZADO DOS NÚMEROS RACIONAIS
Sabemos que a Matemática está relacionada à nossa vida desde os primeiros anos e que
sem ela, é como se alguém que sabe ler e escrever não tivesse completado a sua
alfabetização (MACHADO, 2001).
Essa disciplina até pouco tempo estava sendo lecionada como algo completamente
separado da nossa língua materna, o que não condiz com a realidade, pois as duas
disciplinas têm uma ligação muito grande, assim como outras disciplinas propostas no
currículo da Educação Básica. Além da ligação com as disciplinas estudadas pelos alunos,
a Matemática, ao ser lecionada, tem objetivos muito importantes que vão além de uma
simples resolução de “contas” e cálculos aritméticos.
“A Matemática caracteriza-se como uma forma de compreender e atuar no mundo e o
conhecimento gerado nessa área do saber como um fruto da construção humana
na sua interação constante com o contexto natural, social e cultural”. (PCN’s:
Matemática, 1998)
Orientações Técnicas já realizadas contemplando o assunto:
1.1- 1ª Orientação de Professor Coordenador – Sobre Avaliação de Aprendizagem
em Processo e Currículo (Na Diretoria de Ensino no dia 10 de fevereiro 2015)
1.2-
Reunião de Diretores ( Na Diretoria de Ensino no dia 18/03/2016) PPT1 e
PPT2.
1.3 Orientação de Polo- Ciclo 1 (realizada nas EE Estudante Edinaldo A. Sales dia
12/04/2016; EE Profª Luzia D. R. Hacl dia 13/04/2016 e EE Profª Maria Odette da S.
L. Frattini no 14 de Abril de 2016).
6
2. Localização no Currículo Oficial do Estado de São Paulo
2.1. ENSINO FUNDAMENTAL – ANOS FINAIS
5 ª série/6 º ano
6 ª série/7 º ano
7 ª série/8 º ano
8 ª série/9 º ano
Volume 1
NÚMEROS NATURAIS
– Múltiplos e divisores.
– Números primos.
– Operações básicas.
– Introdução as potencias.
FRAÇÕES
– Representação.
– Comparação e ordenação.
– Operações.
NÚMEROS DECIMAIS
– Representação.
– Transformação em fração
decimal.
– Operações.
SISTEMAS DE MEDIDA
– Comprimento, massa e
capacidade.
– Sistema métrico
NÚMEROS NATURAIS
– Sistemas de numeração
na
Antiguidade.
– O sistema posicional
decimal.
NÚMEROS INTEIROS
– Representação.
– Operações.
NÚMEROS RACIONAIS
– Representação fracionaria
e decimal.
– Operações com decimais
e frações.
GEOMETRIA/MEDIDA
S
– Ângulos.
– Polígonos.
– Circunferência.
– Simetrias.
– Construções geométricas.
– Poliedros.
NÚMEROS RACIONAIS
– Transformação de
decimais finitos em fração.
– Dizimas periódica e
fração geratriz.
POTENCIAÇÃO
– Propriedades para
expoentes inteiros.
TRATAMENTO DA
INFORMAÇÃO
– A linguagem das
potencias.
ÁLGEBRA
– Equivalências e
transformações de
expressões algébricas.
– Produtos notáveis.
– Fatoração algébrica.
NÚMEROS REAIS
– Conjuntos numéricos.
– Números irracionais.
– Potenciação e radiciação
em IR.
– Notação cientifica.
ÁLGEBRA
– Equações de 2o grau:
resolução e problemas.
– Noções básicas sobre
função; a ideia de
interdependência.
– Construção de tabelas e
gráficos para representar
funções de 1o e 2o graus.
Volume 2
GEOMETRIA/MEDIDA
S
– Formas planas e
espaciais.
– Noção de perímetro e
área de figuras planas.
– Cálculo de área por
composição e
decomposição.
TRATAMENTO DA
INFORMAÇÃO
– Leitura e construção de
gráficos e tabelas.
– Média aritmética.
– Problemas de contagem.
NÚMEROS/
PROPORCIONALIDAD
E
– Proporcionalidade direta e
inversa.
– Razões, proporções,
porcentagem.
– Razões constantes na
Geometria: 𝜋.
TRATAMENTO DA
INFORMAÇÃO
– Gráficos de setores.
– Noções de probabilidade.
ÁLGEBRA
– Uso de letras para
representar um valor
desconhecido.
– Conceito de equação.
– Resolução de equações.
– Equações e problemas.
ÁLGEBRA/EQUAÇÕES
– Equações de 1o grau.
– Sistemas de equações e
resolução de problemas.
– Inequações de 1º grau.
– Sistemas de coordenadas
(plano cartesiano).
GEOMETRIA/MEDIDA
S
– Teorema de Tales e
Pitágoras: apresentação e
aplicações.
– Área de polígonos.
– Volume do prisma
GEOMETRIA/MEDIDA
S
– Proporcionalidade, noção
de semelhança.
– Relações métricas entre
triângulos retângulos.
– Razões trigonométricas.
– O numero π; a
circunferência, o circulo e
suas partes; área do circulo.
– Volume e área do
cilindro.
TRATAMENTO DA
INFORMAÇÃO
– Contagem indireta e
Probabilidade.
7
2.2. ENSINO MÉDIO
1ª série
NÚMEROS E SEQUÊNCIAS
– Conjuntos numéricos.
– Regularidades numéricas:
sequencias.
– Progressões aritméticas,
progressões geométricas;
ocorrências em diferentes
contextos; noções de Matemática
financeira.
FUNÇÕES
– Relação entre duas grandezas.
– Proporcionalidades: direta,
inversa, direta com o quadrado.
– Função de 1o grau, função de 2º
grau; significado e ocorrência em
diferentes contextos.
FUNÇÕES EXPONENCIAL E
LOGARITMICA
– Crescimento exponencial.
– Função exponencial: equações e
inequações.
– Logaritmos: definição,
propriedades, significado em
diferentes contextos.
– Função logarítmica: equações e
inequações simples.
GEOMETRIA-TRIGONOMETRIA
– Razões trigonométricas nos
triângulos retângulos.
– Polígonos regulares: inscrição,
circunscrição; pavimentação de
superfícies.
– Resolução de triângulos não
retângulos: Lei dos Senos e
Lei dos Cossenos.
2 ª série
Volume 1
TRIGONOMETRIA
– Arcos e ângulos; graus e
radianos.
– Circunferência trigonométrica:
seno, cosseno, tangente.
– Funções trigonométricas e
fenômenos periódicos.
– Equações e inequações
trigonométricas.
– Adição de arcos.
MATRIZES, DETERMINANTES E
SISTEMAS LINEARES
– Matrizes: significado e
operações.
– A noção de determinante de
uma matriz quadrada.
– Resolução e discussão de
sistemas lineares: escalonamento
como tabelas, características.
Volume 2
ANÁLISE COMBINATÓRIA E
PROBABILIDADE
– Raciocínio combinatório:
princípios multiplicativo e aditivo.
– Probabilidade simples.
– Arranjos, combinações e
permutações.
– Probabilidades; probabilidade
condicional.
– Triangulo de Pascal e Binômio de
Newton.
GEOMETRIA MÉTRICA
ESPACIAL
– Organização do conhecimento
geométrico: conceitos primitivos,
definições, postulados, teoremas.
– Prismas e cilindros:
propriedades, relações métricas.
– Pirâmides e cones: propriedades,
relações métricas.
– A esfera e suas partes; relações
métricas; a esfera terrestre.
3ª série
GEOMETRIA ANALITICA
– Pontos: distância, ponto médio e
alinhamento de três pontos.
– Reta: equação e estudo dos
coeficientes, retas paralelas e
perpendiculares, distância de
ponto a reta; problemas lineares.
– Circunferências e cônicas:
propriedades, equações,
aplicações em diferentes
contextos.
EQUAÇÕES ALGEBRICAS,
POLINÔMIOS, NÚMEROS
COMPLEXOS
– Equações polinomiais: história,
das fórmulas a análise qualitativa.
– Relações entre coeficientes e
raízes de uma equação polinomial.
– Polinômios: identidade, divisão
por x – k e redução no grau de
uma equação.
– Números complexos: significado
geométrico das operações.
ESTUDO DAS FUNÇÕES
– Panorama das funções já
estudadas: principais
propriedades.
– Gráficos: funções
trigonométricas, exponenciais,
logarítmicas e polinomiais.
– Gráficos: análise de sinal,
crescimento, decrescimento, taxas
de variação.
– Composição: translações,
reflexões, inversões.
ESTATÍSTICA
– Cálculo e interpretação de
índices estatísticos.
– Medidas de tendência central:
média, mediana e moda.
– Medidas de dispersão: desvio
médio e desvio padrão.
– Elementos de amostragem.
8
3. Localização de habilidades referentes nas Avaliações de
Aprendizagem em Processo
AAP – 2011
6º ANO – ENSINO FUNDAMENTAL
Questão 3 - Identificar frações equivalentes.
AAP -2012
6º ANO – ENSINO FUNDAMENTAL
Questões 9 e 10 - Identificar fração como representação que pode estar associada ao significado
parte-todo.
7º ANO – ENSINO FUNDAMENTAL
Questão 1 – Localizar números racionais.
Questão 2 - Resolver problema envolvendo noções de porcentagem.
Questão 8 - Reconhecer números racionais, representados na forma fracionária ou decimal, com
significado parte todo.
Questão 9 - Resolver problemas com números racionais expressos na forma decimal que envolva
o significado da subtração.
Questão 10 - Resolver problemas que envolvam fração.
1º ANO – ENSINO MÉDIO
Questão 4 - Resolver problemas que envolvam equações com coeficientes racionais.
2º ANO – ENSINO MÉDIO
Questão 9 - Resolver problemas que envolvam porcentagem
AAP -2013
1 º Semestre
6º ANO – ENSINO FUNDAMENTAL
Questões 9 e 10 - Identificar fração como representação que pode estar associada ao significado
parte-todo.
7º ANO – ENSINO FUNDAMENTAL
Questão 1 – Localizar números racionais na reta numérica.
Questão 2 - Resolver problema envolvendo noções de porcentagem
Questão 9 - Resolver problemas com números racionais expressos na forma decimal que envolva
o significado da subtração.
Questão 10 - Resolver problemas que envolvam fração.
8º ANO – ENSINO FUNDAMENTAL
Questão 1 - Compreender a relação entre as representações fracionária e decimal de um número.
9
9º ANO – ENSINO FUNDAMENTAL
Questão 1 - Compreender a relação entre as representações fracionária e decimal de um número.
1º ANO – ENSINO MÉDIO
Questão 4 - Resolver problemas que envolvam equações com coeficientes racionais.
2º ANO – ENSINO MÉDIO
Questão 9 - Resolver problemas que envolvam porcentagem.
3º ANO – ENSINO MÉDIO
Questão 8 - Resolver problemas que envolvam porcentagem.
2º Semestre
6º ANO – ENSINO FUNDAMENTAL
Questões 9 e 10 - Identificar fração como representação que pode estar associada ao significado
parte-todo.
7º ANO – ENSINO FUNDAMENTAL
Questão 1 – Localizar números racionais na reta numérica.
Questão 2 - Resolver problema envolvendo noções de porcentagem
Questão 9 - Resolver problemas com números racionais expressos na forma decimal que envolvam
o significado da subtração.
Questão 10 - Resolver problemas que envolvam fração.
8º ANO – ENSINO FUNDAMENTAL
Questão 1 - Compreender a relação entre as representações fracionária e decimal de um número.
9º ANO – ENSINO FUNDAMENTAL
Questão 1 - Compreender a relação entre as representações fracionária e decimal de um número.
1º ANO – ENSINO MÉDIO
Questão 4 - Resolver problemas que envolvam equações com coeficientes racionais.
2º ANO – ENSINO MÉDIO
Questão 9 - Resolver problemas que envolvam porcentagem.
3º ANO – ENSINO MÉDIO
Questão 8 - Resolver problemas que envolvam porcentagem.
AAP -2014
1 º Semestre
6º ANO – ENSINO FUNDAMENTAL
10
Questão 8 - Resolver problemas que envolvem o uso da porcentagem no contexto diário, como
10%, 20%, 25% e 50%.
Questão 9- Explorar diferentes significados das frações.
7º ANO – ENSINO FUNDAMENTAL
Questão 5 - Compreender o significado das frações na representação de medidas não inteiras e
da equivalência de frações.
Questões 9 e 12 - Saber transformar frações em números decimais e vice-versa.
8º ANO – ENSINO FUNDAMENTAL
Questões 1 e 13 - Compreender a relação entre uma fração e a representação decimal de um
número, sabendo realizar de modo significativo as operações de adição, subtração,
multiplicação e divisão com decimais.
9º ANO – ENSINO FUNDAMENTAL
Questão 3 - Compreender a ideia de numero racional em sua relação com frações e as razões.
Questão 4 - Compreender a ideia de numero racional em sua relação com frações e as razoes.
Saber manipular as diversas representações dos números racionais e representa-los na reta real.
2 º Semestre
6º ANO – ENSINO FUNDAMENTAL
Questões 5 e 6 - Saber realizar as operações de adição e subtração de frações de modo
significativo.
Questão 10 - Saber transformar frações em números decimais e vice-versa.
Questão 13 - Compreender o significado das frações na representação de medidas não inteiras
e da equivalência de frações.
7º ANO – ENSINO FUNDAMENTAL
Questões 1 e 4 - Saber realizar operações de adição, subtração, multiplicação e divisão de
frações, compreendendo o significado das operações realizadas.
Questão 2 - Compreender a relação entre uma fração e a representação decimal de um número,
sabendo realizar de modo significativo as operações de adição, subtração, multiplicação e
divisão com decimais.
8º ANO – ENSINO FUNDAMENTAL
Questão 1 - Compreender a ideia de número racional em sua relação com as frações e as razões.
Questão 2 - Conhecer as condições que fazem com que uma razão entre inteiros possa se
expressar por meio de dízimas periódicas; saber calcular a geratriz de uma dízima.
AAP -2015
1 º Semestre
7º ANO – ENSINO FUNDAMENTAL
Questões 11 - Saber transformar frações em números decimais e vice-versa.
11
8º ANO – ENSINO FUNDAMENTAL
Questões 11 - Compreender a relação entre uma fração e a representação decimal de um
número sabendo realizar de modo significativo as operações de adição, subtração, multiplicação
e divisão com decimais.
9º ANO – ENSINO FUNDAMENTAL
Questão 7 - Compreender a ideia de numero racional em sua relação com as frações e as razoes.
Questão 8 - Conhecer as condições que fazem com que uma razão entre inteiros possa se
expressar por meio de dizimas periódicas; saber calcular a geratriz de uma dizima.
AAP -2016
1 º Semestre
6º ANO – ENSINO FUNDAMENTAL
Questões 7 e 8 - Transformar um número misto em fração (e vice-versa).
7º ANO – ENSINO FUNDAMENTAL
Questões 1 e 2 - Identificar informações numéricas que envolvem frações e decimais em
contextos diversificados.
Questões 3 e 4 - Realizar operações de multiplicação e divisão com frações em diferentes
contextos.
Questões 5 e 6 - Resolver problemas aritméticos com frações utilizando a ideia de equivalência.
8º ANO – ENSINO FUNDAMENTAL
Questões 1 e 2 - Relacionar um número racional com um conjunto de frações equivalentes.
Questões 3, 4 e 5 - Localizar números racionais na reta.
Questões 6, 7 e 8 - Reconhecer uma dízima periódica como um número racional.
12
4. Aulas diversificadas.
4.1 Reconhecer a porcentagem como representação da fração
Objetivo(s)
- Reconhecer o significado da porcentagem como representação da fração de uma
quantidade.
Conteúdo(s)
- Porcentagem como representação de uma fração decimal.
Ano(s)
1º
2º
3º
4º
5º
Tempo estimado
Três aulas.
Material necessário
Cópias dos quadriculados da 2ª e da 3ª etapas e cartaz com diferentes frases em que
apareça o símbolo %.
Desenvolvimento
1ª etapa
Com os alunos organizados em duplas, inicie a aula entregando para cada uma as figuras
abaixo:
Peça que os alunos comparem as partes pintadas e que as expressem com frações. É
esperado que, na primeira situação, eles indiquem 1/2 e, na segunda, 50/100.
13
Enquanto os alunos resolvem a atividade proposta, percorra as duplas para observar os
registros que estão sendo realizados. Observe também se há alunos que realizam a
comparação da parte pintada no primeiro quadrado com a parte pintada no segundo.
Nesse caso, faça uma intervenção pedindo que eles realizem uma nova leitura do que a
atividade propõe, comparando o registro que eles fizeram com a questão proposta.
Organize um momento de discussão coletiva do resultado encontrado pelas duplas e
registre-os no quadro. Questione se os registros matemáticos que se referem à
comparação da parte com o todo estão representados por um mesmo número. Peça
que a garotada compare os quadrados pintados, justapondo-os. Instigue-os a explicar o
que ocorre com as representações pictóricas. Observe se na explicitação dos alunos
aparece a afirmação de que, apesar da comparação das partes com o todo serem
indicadas por frações diferentes, elas se equivalem.
2ª etapa
Entregue para cada criança uma cópia dos quadrados representados a seguir:
Pergunte aos alunos quais são as frações que relacionam a parte pintada, em cada
quadrado, com o todo. Em seguida, peça que comparem os registros realizados com os
quadrados representados para estabelecer relações entre eles. Na conclusão desta
etapa, é esperado que as crianças reconheçam a equivalência entre as escritas 1/4 e
25/100.
3ª etapa
Disponha no quadro um cartaz com diferentes frases em que aparecem o símbolo %.
Diga que há um símbolo matemático presente em todas e pergunte se eles identificam
que símbolo é esse. Explique que o sinal % significa por cento e que porcentagem indica
uma parte em relação a 100. Pergunte como representar em porcentagem 1/100; 7/100;
40/100 etc.
14
4ª etapa
Exponha novamente o cartaz exibido na 3ª etapa, retome as informações sobre
porcentagem e pergunte como representar a fração 25/100. Questione os alunos se 1/4
pode ser representado por 25%. Ouça as opiniões dos alunos e analise, junto com eles,
cada hipótese. A conclusão deve ser a de que é possível registrar ambas as frações como
25%, pois se equivalem.
5ª etapa
Com a turma dividida em duplas, forneça valores na forma porcentual "rasa" - por
exemplo, 10%, 20% etc. - e peça aos alunos que encontrem sua representação
fracionária. Lembrese de que eles podem apresentar diferentes registros: para 20%,
20/100, 2/10 ou 1/5. Socialize as respostas.
Avaliação
Observe se a garotada compreendeu as seguintes relações: 50% equivale a 1/2, 25%
corresponde a 1/4 e 10% é equivalente à décima parte. Essas relações são fundamentais
para o aprendizado de porcentagem.
Flexibilização
Estabeleça objetivos específicos (de acordo com o desenvolvimento do aluno) para
analisar a aprendizagem individualmente.
1ª etapa
Faça dupla com o estudante ou o agrupe a um colega que favoreça sua atuação e
aprendizagem.
Retome com o aluno o registro da fração - o que representamos no numerador e no
denominador. Dê alguns exemplos para que ele aplique seus conhecimentos sobre o
conteúdo.
2ª etapa
Observe como o aluno realiza a contagem dos quadradinhos do diagrama acima e à
esquerda. Se houver dificuldade, oriente-o a riscar os 10 quadradinhos da primeira
linha, conforme for contando, e o acompanhe na contagem de 10 em 10 do restante
das fileiras.
3ª etapa
Ao apresentar essas frações, adapte um registro com os diagramas ao lado de cada
fração, deixe as primeiras para que ele complete o numerador e as últimas o
denominador.
4ª etapa
Converse com o aluno e explique a importância de se dedicar ao que será proposto
15
pelo professor. Proponha exercícios semelhantes ao anterior para que desenvolva a
contagem, o registro e a leitura de frações.
5ª etapa
Apresente diferentes frações para que sejam relacionadas aos diagramas
correspondentes e frações equivalentes que provoquem seu raciocínio.
4.2 Jogo da Memória de Números Racionais
Material: confeccionar baralho com trios de números racionais escritos na forma
decimal, percentual e fracionária.
Número de jogadores: de 2 a 4
Objetivo: Conseguir o maior número de trios de números racionais com diferentes
representações.
Como jogar: Embaralhe as cartas e coloque-as na mesa com as faces escritas voltadas
para cima. Os jogadores observam as cartas por alguns segundos, tentando identificar
trios de racionais. A seguir, vire as faces escritas para baixo. O primeiro jogador desvira
três cartas. Se elas formarem trio, ele as retira da mesa e joga novamente. Se não, volta
a virá-las com as faces escritas para baixo, deixando-as no mesmo lugar na mesa.
O jogo continua até que todas as cartas sejam retiradas da mesa.
Vence o jogador que conseguir o maior número de trios de cartas. Também se pode
variar o jogo formando pares ou trios de representações gráficas e numéricas de frações,
leitura e escrita numérica, operações e resultados.
4.3 Jogo Papa Todas
Objetivos: Compreender o conceito de fração; comparar frações com diferentes
denominadores; noção de equivalência de frações; leitura e representação de frações;
resolução de problemas que envolvam frações e realizar cálculo mental com frações.
Sugerimos que você não ensine as regras para comparar frações, mas deixe que utilize
as regras de comparar frações, mas deixe que utilizem as réguas de fração para criar
formas próprias de comparar e depois favoreça discussões nas quais essas regras
apareçam e sejam socializadas para todos.
Distribua o material do jogo (as cartas e a tabela de tiras de frações) e proponha aos
alunos que, em grupos de 4, analisem o mesmo:
• O que mostram as cartas?
• Que relação há entre as cartas e a tabela de frações?
• Quem consegue mostrar cartas com frações menores que 1 inteiro? Faça uma lista na
lousa.
• Quem consegue mostrar cartas que sejam menores que ½?
16
• Peça uma carta maior que um inteiro e como eles decidiram isso. Faça uma lista na
lousa
• Mostre uma fração nas barras e então peça que localizem uma carta correspondente
a ela. Fique atenta porque pode ter mais que uma resposta em função de frações
equivalentes tais como 1/2, 2/4, 3/6...
Regras:
• O jogo é para grupos de 4 a 5 alunos (não sugerimos duplas porque ele perde o sentido
de desafio)
• Todas as cartas do baralho são distribuídas entre os jogadores que não vêem suas
cartas. Cada jogador coloca suas cartas em uma pilha com os números virados para
baixo.
• A tabela com as tiras de fração é colocada no centro da mesa de modo que todos a
vejam.
• Os jogadores combinam entre si um sinal ou uma palavra. Dado o sinal todos os
jogadores viram a carta de cima de sua pilha ao mesmo tempo e comparam as frações.
O jogador que tiver a carta representando a maior fração vence a rodada e fica com
todas as cartas (Papa Todas).
• A tabela de tiras de frações pode ser usada se necessário para que as comparações
sejam feitas.
•Se houver duas cartas de mesmo valor todas as cartas ficam na mesa e na próxima
rodada o jogador com a maior carta papa todas, inclusive aquelas que estão na mesa.
• O jogo termina quando as cartas acabarem.
Quem ganha: O jogador com o maior número de cartas
A cada vez que os alunos jogarem, proponha uma ação diferente de exploração do jogo,
conforme sugerimos a seguir.
Após os alunos jogarem você pode propor problemas para eles resolverem, por
exemplo:
1 - Numa rodada Humberto tirou 1/5, Cristiane tirou 4/8, Olga tirou 3/3 e Bruna 5/10.
Quem ganhou o jogo? Como vocês sabem?
2 - Patrícia tirou 1/2, Ellen tirou 4/8, Pedro tirou 7/7 e Aline ganhou a partida. Qual carta
ela pode ter tirado? Procure observar que há aqui um problema com mais de uma
solução possível.
3 - Julia virou 2/4, Flávio tirou 4/8, Beto 3/6 e Otávio tirou 1/3. Quem venceu a partida?
4 - Durante o jogo os alunos organizaram uma tabela com as frações que cada um tirou.
Quem ganhou o maior número de rodadas?
Jogador 1ª rodada 2ª rodada 3ª rodada 4ª rodada
Júlia 2/4 1/2 8/6 7/3
Paulo 10/10 1/4 3/6 4/10
Luís 4/4 1/3 6/8 3/9
5 - Quais as cartas que contêm frações equivalentes a 1 inteiro?
6 - Em uma rodada Paulo, Ana e Renato tiraram as seguintes cartas: ½; 4/8 e 3/6. Eles
começaram a discutir sobre quem conseguiu a maior carta. Se você estivesse nessa
discussão, como os ajudaria a tomar a decisão sobre qual é a maior carta?
7 - Use a tabela com as barras de fração e compare as semelhanças e diferenças entre
os seguintes pares de fração:
3/6 e 6/3 ; 3/7 e 7/3 ; 8/6 e 6/8
17
4.4 - Jogo do Pare de Frações
Material: tabela, lápis e borracha.
Número de participantes: qualquer quantidade (a partir de 2 )
Objetivo: Realizar todos os cálculos para descobrir frações que representam partes de
quantidades, o mais rápido possível, a partir de números escolhidos.
Como jogar: O professor ditará um número, que deverá ser escrito no 1º quadrinho da
1ª coluna, indicando que o jogo começou. Você deve representar as partes desse
número indicadas pelas frações, que se encontram na lª linha, colocando os resultados
nos respectivos espaços. O primeiro que encontrar a quantidade de todas as partes fala
“pare” e todos os participantes devem parar. O professor faz a correção no quadro e
para cada acerto você ganhará 5 pontos. Marque seus pontos no final da tabela. Vence
aquele que obtiver o maior número de pontos ao final de algumas rodadas.
Faça uma tabela como esta para registrar suas jogadas.
Número ditado 1/2 1/4 3/4 1/3 2/3 1/5 2/5 Pontos
480 240 120 360 160 320 96 192 40
Jogo da Trilha cem por cento
Número de participantes: 2 a 4
Material: tabuleiro, dado e botões coloridos ou peões.
Regras: Todos os peões são colocados na “partida”. Joga-se o dado e quem tirar o maior
número inicia o jogo. Joga-se novamente o dado e o peão anda tantas casas quantas o
resultado da jogada indicar. Caso o peão caia numa das casas especiais, deve-se
obedecer ao comando ali escrito. Para vencer, é necessário tirar o número exato de
pontos que faltam para a “chegada”. Se o nº sorteado for superior ao necessário, devese retornar tantas casas quantos forem os pontos excedentes.
4.5 Jogo da Memória dos Números Racionais.
O Jogo Da Memória dos Números Racionais, conforme figura 2, deste artigo foi
confeccionado com materiais recicláveis. O objetivo do jogo é compreender que os
números racionais são representados nas formas simbólico-numéricas (decimal,
percentual e fracionária), língua escrita (por extenso) e figural (desenhos). O material
deste jogo foi usado com 30 cartas de baralho com números racionais escritos nas
formas simbólico-numéricas, língua escrita e figural. Os participantes do jogo são de 2 a
4 jogadores. Embaralhe as cartas e coloque-as na mesa com as faces escritas voltadas
para cima. Os jogadores observam as cartas por alguns segundos, tentando identificar
trios de racionais. A seguir, vire as faces escritas para baixo. O primeiro jogador desvira
três cartas. Se elas formarem trio, ele as retira da mesa e joga novamente. Se não, volta
a virá-las com as faces escritas para baixo, deixando-as no mesmo lugar na mesa. O jogo
18
continua até que todas as cartas sejam retiradas da mesa. Vence o jogador que
conseguir o maior número de trios de cartas. Pode-se variar o jogo formando pares ou
trios de representações para operações e resultados.
4.6 Jogo da Memória das Frações Equivalentes
O Jogo Da Memória das Frações Equivalentes, conforme figura 3, deste artigo foi
confeccionado com materiais recicláveis. O objetivo é compreender as frações
irredutíveis e suas frações equivalentes.
Foram usadas 30 cartas de baralho com frações escritas nas formas e suas
equivalentes.
Os participantes do jogo são de 2 a 4 jogadores.
Embaralhe as cartas e coloque-as na mesa com as faces escritas voltadas para cima. Os
jogadores observam as cartas por alguns segundos, tentando identificar as frações e
suas equivalentes. A seguir, vire as faces escritas para baixo. O primeiro jogador
desvira duas cartas. Se elas formarem a fração equivalente correspondente a outra
fração, ele as retira da mesa e joga novamente. Se não, volta a virá-las com as faces
escritas para baixo, deixando-as no mesmo lugar na mesa. O jogo continua até que
todas as cartas sejam retiradas da mesa. Vence o jogador que conseguir o maior
número de dupla de cartas.
19
20
5. Banco de dados
Relatório Pedagógico SARESP 2008
Relatório Pedagógico SARESP 2009
21
22
23
Relatório Pedagógico SARESP 2010
24
25
Relatório Pedagógico SARESP 2011
26
27
Relatório Pedagógico SARESP 2012
28
29
Relatório Pedagógico SARESP 2013
30
Relatório Pedagógico SARESP 2014
31
32
6. Bibliografia










Texto inicial de Josemary Peixoto Dantas (acesso em 27 de junho de 2016 as
10:30h)
MACHADO, Nilson José. Matemática e Realidade: análise dos pressupostos
filosóficos que fundamentam o ensino da Matemática. São Paulo: Cortez:
Autores filiados, 1987.
MENDES, Jackeline Rodrigues et al. Números Racionais no Ensino Fundamental:
subconstructos, o papel da linguagem e dos materiais manipulativos. NEPEM
(Núcleo de Estudos e Pesquisas em Educação Matemática). VIII Encontro
Nacional de Educação Matemática. UFPE. Recife, 2004.
São Paulo (Estado) Secretaria da Educação. Caderno do Professor: Matemática,
ensino fundamental – 5ª a 8ª séries. Volumes 1 a 4. Coordenação geral: Maria
Inês Fini; equipe, Carlos Eduardo de Souza Granja, José Luiz Pastori, Nilson José
Machado, Roberto Pérides Moisés, Rogério Ferreira da Fonseca, Ruy César
Pietropaolo, Walter Spinelli. – São Paulo: SEE, 2009.
São Paulo (Estado) Secretaria da Educação. Coordenadoria de Estudos e Normas
Pedagógicas. Experiências Matemáticas: 5ª a 8ª séries. São Paulo: SE / CENP,
1997.
GRASSESCHI, Maria Cecília C. PROMAT: projeto oficina de matemática/ Maria
Cecília C.Grasseschi, Maria Capucho Andretta, Aparecida Borges dos Santos Silva.
_ São Paulo: FTD, 1999 (volume 2)
PADOVAN, Daniela. Matemática: ensino fundamental/ Daniela Padovan, Isabel
Cristina Ferreira guerra, Ivonildes dos Santos Milan _ 1 ed. _ São Paulo: Moderna,
2001 ( 4ª série)
LARA, Isabel Cristina Machado de. Jogando com a Matemática de 5ª à 8ª série/
Isabel Cristina Machado de Lara. _ 1. ed. _São Paulo: Rêspel, 2003.
SPINELLI, Walter. Matemática. Walter Spinelli e Maria Helena Soares de Souza.
São Paulo:Ática, 2004.(Série Brasil)
Lista
Resolvida
de
Números
Racionais.
Disponível
em:
http://pt.slideshare.net/missblef/lista-resolvida-de-nmeros-racionais. Acesso
em 25 de maio de 2016.
33