Sebenta - DEC/FCT/UNL

Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Vibrações mecânicas
1. Introdução
Entende-se por vibração o movimento repetitivo de uma partícula, de um corpo ou do
conjunto de corpos em torno de uma posição de equilíbrio estático estável. Quando os
deslocamentos realizados por este sistema forem pequenos, a vibração designa-se pequena.
Usa-se assim a teoria das pequenas vibrações ou oscilações.
A origem das vibrações
Foi explicado no capítulo PTV que um sistema na posição de equilíbrio estável, quando sujeito
a uma perturbação desloca-se dessa posição, mas retirando a causa desta perturbação, volta à
sua posição de equilíbrio estável. Isso iria acontecer se essa volta fosse feita de maneira quase
estática, ou seja de modo lento, sem activação de efeitos de inércia. Na realidade isso não
acontece e o sistema volta à posição de equilíbrio estável, mas naquele instante tem um certa
velocidade que o obriga a ultrapassar essa posição (veja também o problema da dinâmica em
que foi calculada a velocidade do sistema na posição de equilíbrio estável). O sistema deslocase assim para outro lado até diminuir a velocidade a zero, depois tenta voltar novamente à
posição de equilíbrio estável e atinge esta posição novamente com uma certa velocidade, etc.
As vibrações em geral representam efeitos não desejáveis, porque induzem o aumento de
tensões, perdas de energia, desgaste de material, etc.
Termos
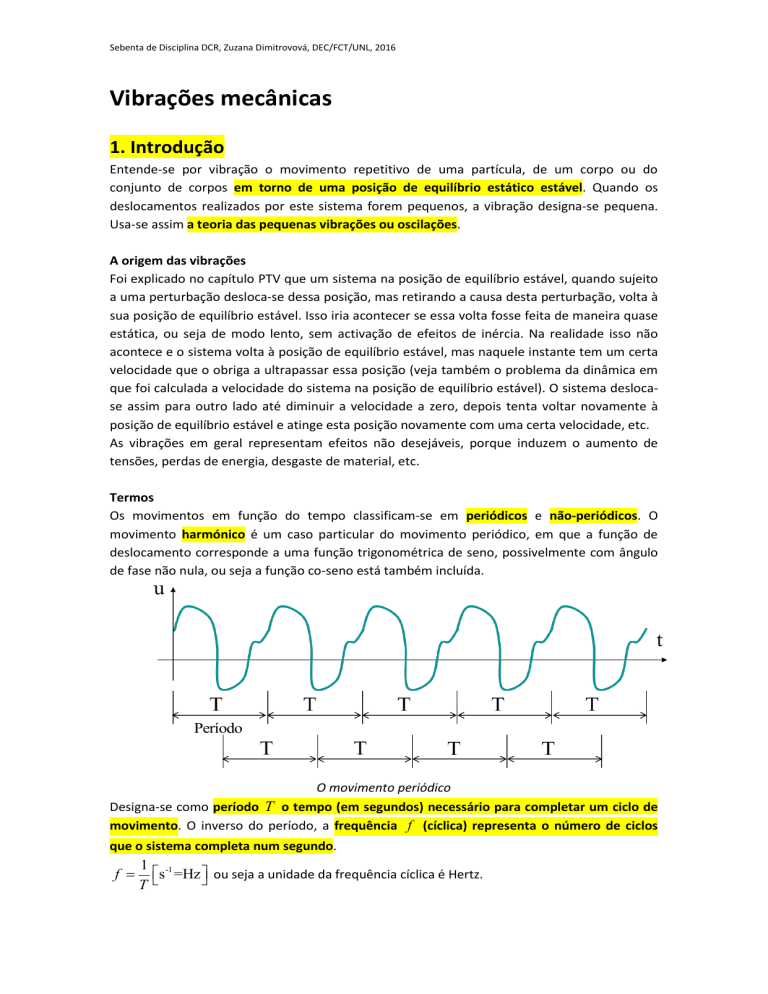
Os movimentos em função do tempo classificam-se em periódicos e não-periódicos. O
movimento harmónico é um caso particular do movimento periódico, em que a função de
deslocamento corresponde a uma função trigonométrica de seno, possivelmente com ângulo
de fase não nula, ou seja a função co-seno está também incluída.
Período
O movimento periódico
Designa-se como período T o tempo (em segundos) necessário para completar um ciclo de
movimento. O inverso do período, a frequência f (cíclica) representa o número de ciclos
que o sistema completa num segundo.
f 
1 -1
s =Hz  ou seja a unidade da frequência cíclica é Hertz.
T
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
u
t
O movimento não-periódico
Amplitude
O movimento harmónico
O deslocamento máximo chama-se a amplitude; num movimento periódico a amplitude dos
deslocamentos positivos pode ser diferente da amplitude dos deslocamentos negativos.
Os adjectivos: periódico, não-periódico e harmónico usam-se igualmente junto com as forças,
velocidades, aceleração, etc, porque apenas descrevem o andamento de alguma função em
relação ao tempo.
Neste capítulo apenas os mecanismos com 1GDL serão abordados. A equação que descreve o
movimento oscilatório é uma equação diferencial que corresponde à equação de movimento
(equilíbrio dinâmico na direcção da variável do movimento). As incógnitas neste caso serão
funções de variável tempo: u  t  , v  t  , a  t  ou   t  ,   t  ,   t  , no entanto a por razões
de simplificação o argumento t costuma-se omitir. Para se destacar a dependência no tempo e
assim indicar o grau da equação diferencial, costuma-se escrever
u, v 
du
d
d 2
d 2u
u, a 2 u e  ,  
 ,   2 
dt
dt
dt
dt
Vibrações livres não amortecidas
O movimento é mantido apenas pelas forças de restituição, ou seja pelas forças inerentes ao
sistema (que são por exemplo: as forças elásticas das molas e as forças gravíticas). A
perturbação que inicia o movimento corresponde a um deslocamento e/ou a uma
velocidade aplicada ao sistema, não há forças exteriores aplicadas ao sistema. Neste caso,
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
todos os termos envolvidos na equação que descreve o movimento tem que conter a
variável do movimento (equação homogénea). A vibração chama-se natural. Não se
considera qualquer tipo de atrito ou outra perda de energia, a vibração dura para sempre
sem qualquer alteração.
Vibrações forçadas não amortecidas
Além das forças de restituição, existem as forças externas aplicadas ao sistema. Estas forças
serão somente consideradas na forma harmónica. As forças constantes que permanecem no
sistema afectam a posição de equilíbrio estável e não contribuem à manutenção do
movimento oscilatório. As forças de curta duração, constantes ou com outra evolução, ou seja
os impulsos das forças, ultrapassam o âmbito desta sebenta. O movimento oscilatório neste
regime corresponde à sobreposição de dois movimentos, um que corresponde à vibração
natural e outro à vibração forçada. Não se considera qualquer tipo de atrito ou outra perda
de energia, a vibração dura para sempre sem qualquer alteração. A vibração forçada pode ser
igualmente originada e mantida pelo movimento harmónico da base do sistema.
Vibrações livres amortecidas
O movimento é mantido apenas pelas forças de restituição, no entanto consideram-se as
perdas de energia, via forças de atrito (interno ou externo) chamadas também as forças de
amortecimento, por isso o movimento vai diminuir a sua amplitude, até cessar. Teoricamente
cessa no tempo infinito, mas o decréscimo de amplitude é exponencial.
Vibrações forçadas amortecidas
Além das forças de restituição existem as forças oscilatórias externas aplicadas ao sistema, no
entanto consideram-se as perdas deu energia. As perdas de energia afectam principalmente a
vibração natural, que cessa passado algum tempo. O amortecimento afecta a amplitude da
vibração forçada, mas esta dura para sempre. Visto a vibração estar composta pela
sobreposição destas duas partes, costumam-se introduzir os termos: o regime transiente
(transitório) que corresponde ao intervalo de tempo inicial, em que ainda há vibração natural
não desprezável. O outro regime começa quando a vibração natural é desprezável, e assim o
movimento é composto apenas pela parte forçada, e por isso o regime chama-se estacionário,
ou seja representa a estabilização do sistema no movimento que se repete sem qualquer
alteração até quando actuarem as forças externas.
u
Vibração livre não-amortecida Vibração livre amortecida (período ligeiramente maior)
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
u
Vibração forçada não-amortecida
verde: contribuição natural
azul: contribuição forçada
vermelho: vibração total
u
u
Intervalo de tempo inicial (regime transitório)
Intervalo de tempo intermédio (regime transitório)
Vibração forçada amortecida
u
verde: contribuição natural
azul: contribuição forçada
vermelho: vibração total
Regime estacionário
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
2. Corpo rígido com único movimento
Vibrações lineares
Quando um corpo rígido (possivelmente composto por vários corpos elementares) oscila sobre
uma posição de equilíbrio estável efectuando o movimento de translação, a vibração chama-se
linear. A variável que caracteriza este movimento é o deslocamento. A equação que rege a
vibração determina-se via equação de movimento, ou seja via equação do equilíbrio dinâmico,
que neste caso, contrariamente ao Capítulo Dinâmica, tem que se escrever na posição
deformada e apenas no sentido de movimento (somatório de forças).
Vibrações rotacionais
Quando um corpo rígido (possivelmente composto por vários corpos elementares) oscila sobre
uma posição de equilíbrio estável efectuando o movimento de rotação em torno de um ponto
fixo (CIR fixo, centro de rotação, C ), a vibração chama-se rotacional. A variável que
caracteriza este movimento é o ângulo de rotação, que neste caso chama-se a coordenada
generalizada. O movimento descreve-se com uma única equação que corresponde ao
equilíbrio dinâmico dos momentos em torno do ponto fixo C (equação do movimento na
posição deformada). Tal como explicado no capítulo de Dinâmica, quando não se usam as
equações que representam o equilíbrio das forças, há possibilidade de usar o único momento
de inércia na forma I C .
Durante as vibrações rotacionais, cada ponto do sistema faz igualmente a vibração linear. A
transferência faz-se do mesmo modo como se traduziam deslocamentos infinitesimais para a
rotação, e ainda será necessário alterar o equilíbrio dos momentos para o equilíbrio das
forças na direcção do movimento.
Métodos de resolução
Para resolver as vibrações, escreve-se primeiro a equação de movimento (a equação do
equilíbrio dinâmico) na direcção da vibração. As equações de movimento explicadas no
capítulo de Dinâmica escreveram-se na posição indicada (analisada) sem alguma introdução
da deformada, neste capítulo o equilíbrio tem que se escrever na posição deformada, no
entanto esta deformação considera-se infinitesimal, porque as vibrações são pequenas, por
isso a deformada obedece às normas usadas para traçar o campo de deslocamentos virtuais.
A actuação de variáveis de movimento (deslocamento no caso das vibrações lineares e
ângulo no caso da vibrações rotacionais) e consequentemente de velocidade e aceleração ou
velocidade angular e aceleração angular assume-me com actuação num único sentido,
seleccionado como sentido positivo, porque isso é obrigatório para formalizar as deduções
matemáticas. Depois de ter a equação que rege a vibração, é necessário resolve-la para
obter as variáveis de movimento oscilatório em função de tempo. No entanto, para a
formalização dos campos de variáveis finais, podem usar-se fórmulas deduzidas da equação
genérica.
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
2.1 Vibrações lineares
2.1.1 Dedução da equação que rege a vibração
Assume-se uma partícula (massa concentrada) tal como se visualiza na figura abaixo
Equação do movimento (equilíbrio dinâmico) numa posição intermédia u
ma  mg  k u est u   0
Equilíbrio estático
mg  kuest  0
Juntando as duas equações
ma  ku  0 ou seja
mu  ku  0
que é uma equação diferencial (ordinária) de segunda ordem homogénea. Neste caso notouse que o peso da partícula não contribuiu às forças de restituição, a única força de restituição é
a força elástica da mola. O facto de considerar o peso ou não será de grande importância. Em
casos de dúvida procede-se de duas maneiras: (i) escrevem-se as duas formas de equilíbrio,
estático e dinâmico e juntam-se as duas equações numa só; (ii) usa-se directamente o facto de
a equação resultante só poder conter os termos que contém a variável do movimento na sua
forma original ou sujeita a derivada de tempo; por esta razão é possível remover todos os
termos restantes (absolutos).
O caso seguinte mostra que em algumas situações o peso do sistema nem entra na equação
do movimento, que se escreve na direcção do movimento oscilatório. Nota-se que como se
trata de vibrações não-amortecidas, não há perdas de energia e por isso as forças de atrito
estão desprezadas. Neste caso na direcção do movimento actua apenas a força de inércia e a
força elástica da mola. Recorda-se que a equação de equilíbrio dinâmico deve-se escrever na
posição deformada, no entanto, no caso da partícula não se nota esta diferença.
Directamente
mu  ku  0
ku
ma
mg
N
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Realça-se que as forças de inércia e as forças elásticas das molas actuam sempre no sentido
de voltar o sistema à sua posição de equilíbrio.
2.1.2 Resolução da equação diferencial
A equação mu  ku  0 chama-se equação canónica. A sua resolução começa por divisão pela
massa:
u
k
u0
m
Assume-se a solução na forma u  et . Substituindo e simplificando
2 
k
 0 que se chama a equação característica
m
As raízes da equação característica são: 1,2  i
k
k
, ou seja, designando n 
m
m
frequência circular (angular) natural de unidade rad/s, a solução da equação acima tem a
forma:
u  C1 cos nt   C2 sin nt 
Para esta representação usou-se a fórmula de Euler:
eix  cos  x   isin  x 
ou seja a forma original da solução alterou-se de acordo com a dedução abaixo
C1ein +C2e-in  C1 cos n   iC1 sin n  +C2 cos n  -iC2 sin n 




 C1  C2 cos n  +i C1 -C2 sin n   C1 cos n  +C2 sin n 
Esta representação tem a vantagem de definir directamente o movimento harmónico no
domínio dos números reais. Ver-se-á em seguida que as constante C1 e C2 serão sempre
números reais.
A ligação entre a frequência cíclica e circular é n  2 fn , porque 2 representa uma volta
completa medida em radianos.
A fórmula para o cálculo da frequência indica que: um aumento de massa e/ou a diminuição
de rigidez causa a diminuição da frequência ou seja, o aumento do período (oscilação mais
lenta), um aumento de rigidez e/ou a diminuição de massa causa o aumento da frequência,
ou seja a diminuição do período (oscilação mais rápida).
As constantes C1 e C2 determinam-se das condições iniciais do movimento. As condições
iniciais não podem ser ambas nulas, porque representam o “impulso” que iniciou o
movimento, este “impulso” pode ter a forma de deslocamento ou velocidade (ou ambos)
iniciais, designados u0 e v0 , ou seja
u  0  u0  C1 cos n  0  C2 sin n  0  C1
v  0   v0 
d
 C1 cos nt   C2 sin nt   t 0  n  C1 sin n  0  C2 cos n  0   nC2
dt
Assim
u  u0 cos nt  
v0
n
sin nt 
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
A solução pode representar-se na forma compacta:
u  u0 cos nt  
v0
0
v0
 cos  &
Aun
sin nt   Au  cos nt  sin   sin nt  cos    Au sin nt   
u0
u
 sin   tan   0 n
Au
v0
v 
& Au  u   0 
 0 
2
2
0
Na formulação acima Au representa a amplitude dos deslocamentos e  ângulo de fase.
Estes cálculos não aplicam todos os sinais correctamente e por isso de todas as soluções da
função arctan é necessário escolher a correcta. A escolha faz-se de acordo com o sinal da
função resultante no tempo nulo. Ou seja u0 tem que ter o mesmo sinal como sin  .
Admitindo   arctan
u0n
:    quando v0  0 , e      quando v0  0 . Quando
v0
v0  0 ,    / 2 ou seja u  u0 cos nt  já com o sinal correcto.
Tn
O movimento oscilatório pode ser representado registando a ordenada vertical do ponto
que está a fazer o movimento circular com o raio igual à amplitude, o ângulo inicial igual ao
ângulo de fase e a velocidade angular igual à frequencia circular natural. O movimento
chama-se movimento harmónico simples.
Os gráficos representados abaixo indicam as 4 posibilidades de sinais de u0 e v0 .
u
u0  0, v0  0
 0
 
     0, 
 2
sin   0
u
u0  0, v0  0
 0
 
       , 
2 
sin   0
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
u
u0  0, v0  0
 0
  
      ,0 
 2 
sin   0
u
u0  0, v0  0
 0
 3 
      ,  
 2 
sin   0
2.1.3 Rigidez equivalente
Molas
Recorda-se que a actuação real da força elástica sobre a partícula (corpo) em que está
colocada é sempre contra o movimento efectuado (no sentido para voltar a partícula/corpo
à sua posição inicial). Por esta razão é indiferente de que lado da estrutura a mola está
colocada.
A ligação em paralelo implica o deslocamento igual em todas as molas; de equilíbrio segue que
a força elástica da mola equivalente é igual à soma das forças elásticas das molas envolvidas e
por isso a rigidez equivalente, equivale à soma de rigidezes envolvidas.
Fe,eq  Fe1  Fe2  Fe3
kequ  k1u  k2u  k3u  keq  k1  k2  k3
A ligação em série implica a força elástica igual em todas as molas, que também equivale à
força elástica da mola equivalente.
Fe,eq  Fe1  Fe 2 , kequ  k1u1  k2u2
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
O deslocamento total é igual à soma dos deslocamentos das molas envolvidas. A igualdade das
forças elásticas permite exprimir os deslocamentos
keq
u  u1  u2  u 
k1
u
keq
k2
u
ou seja
1 1
keq     1 
 k1 k2 
1
1 1
 
keq k1 k2
 keq 
k1k2
k1  k2
Pode-se assim concluir que o inverso de rigidez equivalente, equivale à soma de inversos de
rigidezes envolvidas (a flexibilidade equivalente equivale à soma de flexibilidades
envolvidas). Esta relação pode ser extendida a mais do que 2 molas
1
1 1 1
    ...
keq k1 k2 k3
Elementos flexíveis
A oscilação da extremidade de uma consola pode ser também analisada via uma mola
equivalente. A rigidez desta mola define-se da analogia com a força elástica como o inverso do
deslocamento provocado pela força unitária. Como os deslocamentos assumem-se pequenos,
é válida a linearidade, ou seja o deslocamento é proporcional à força aplicada, tal como a força
elástica.
2.1.4 Sobre a resolução da equação diferencial
Todos os casos das vibrações lineares são regidos pela equação (a unidade dos termos
envolvidos na equação é a unidade da força [N ou kN]):
mequ  kequ  0
Após a determinação da equação de movimento que rege a vibração, basta agrupar os termos
para se determinar meq  0 [kg ou ton] e keq  0 [N/m ou kN/m] (ambos positivos), ou seja,
basta juntar os coeficientes das variáveis com a mesma ordem de derivada de tempo e usar
as resoluções pré-calculadas:
u  u0 cos nt  
v0
n
sin nt  ou
2
v 
u
u  Au sin nt    , onde Au  u   0  e   arctan 0 n
v0
 0 
2
0
(quando v0  0     , quando v0  0       )
Pelas derivadas em ordem de tempo obtem-se:
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
v  u0n sin nt   v0 cos nt  ou
v  Aun cos nt    , ou seja Av  Aun
a  u0n2 cos nt   v0n sin nt  ou
a   Aun2 sin nt    , ou seja Aa  Avn  Aun2
Comparando o andamento de deslocamento, velocidade e aceleração, realça-se que neste
caso o período (ou frequência) e o ângulo de fase mantêm-se inalterados, apenas a
amplitude sofre alterações como indicado. A aceleração está descrita pela mesma função
como os deslocamentos, mas com o sinal oposto. Os extremos de deslocamentos e
acelerações ocorrem nos mesmos instantes de tempo, nomeadamente nos instantes em que
a velocidade é nula. Os extremos de velocidades ocorrem nos instantes em que os
deslocamentos e acelerações são nulos.
u...verde
v...azul
a...vermelho
Au  3m
n  2rad/s
  0, 2rad
Tn    3,14s
Na figura acima as rectas verticais pretas mostram que o máximo (no valor absoluto) de
velocidade ocorre nos tempos em que o deslocamento e a aceleração são nulos, ou seja
quando a estrutura passa pela posição de equilíbrio. As rectas pretas tracejadas mostram
que quando a velocidade é nula, o deslocamento e a aceleração são máximos (no valor
absoluto). Nestas posições a velocidade vira o seu sentido e a estrutura começa a voltar à
sua posição de equilíbrio. A aceleração actua na direcção do movimento, ou seja, o
movimento é acelerado, porque na posição do equilíbrio a velocidade tem que atingir o seu
máximo. Quando esta posição é ultrapassada, o movimento começa a desacelerar, até a
velocidade atingir o valor nulo, no lugar do próximo deslocamento máximo (no valor
absoluto).
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Problema
Um bloco com massa 50kg está apoiado pelo conjunto de
molas tal como visualizado na figura ao lado, com k1= 10kN/m,
k2= 15kN/m e k3 = 8kN/m. O bloco é deslocado verticalmente
para baixo 3cm e em seguida libertado. Admitindo que não há
atrito entre o bloco e as paredes, determine:
a) o período e a frequência circular do movimento;
b) a velocidade máxima e a aceleração máxima do bloco.
Resolução
As várias molas aplicadas ao bloco podem ser substituídas por uma única mola equivalente, as
relações da sua definição não são necessárias deduzir novamente, basta utilizar as fórmulas já
preparadas, ou seja, na ligação em paralelo a rigidez final equivale à soma das rigidezes e na
ligação em série a inversa de rigidez final equivale à soma das inversas de rigidezes.
Como já justificado, não é importante considerar a posição exacta das molas, podem
considerar-se todas as molas colocadas abaixo do bloco, a rigidez total das molas corresponde
às 4 molas em paralelo em que duas destas molas representam a ligação em série. Assim a
rigidez desta é:
kk
1
 1 2 e assim:
1 1 k1  k2

k1 k2
keq  k2  k3  2
k1k2
 35kN/m
k1  k2
a) Usando o formulário: n 
keq
M

35000
2
 26, 46rad/s , Tn 
 0, 237s
50
n
b) Usando o formulário: u  u0 cos nt  , ou seja Au  u0  0,03m
a velocidade máxima corresponde à amplitude: Av  u0n  0,794m/s
a aceleração máxima corresponde à amplitude: Aa  u0n2  21m/s2
2.2 Vibrações rotacionais
2.2.1 Centro de rotação fixo
Admite-se que um corpo rígido (possivelmente composto por vários corpos elementares)
oscila sobre uma posição de equilíbrio estável efectuando o movimento de rotação em torno
de um ponto fixo (CIR fixo, centro de rotação, C ). A variável que caracteriza este movimento é
o ângulo de rotação  .
A equação que rege as vibrações corresponde à equação do equilíbrio dinâmico (equação de
movimento), na direcção da variável  , ou seja, ao equilíbrio dos momentos em torno C , que
é também a única equação de equilíbrio que não envolve as reacções externas. Em primeiro
lugar é necessário colocar correctamente as forças de inércia, mas como justificado no capítulo
de Dinâmica, no movimento circular as componentes das forças de inércia resultantes das
componentes normais de aceleração têm as linhas de acção que passam pelo centro de
rotação. Neste caso, tal como explicado no capítulo de Dinâmica, quando não se usam as
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
equações que representam o equilíbrio das forças (o somatório das forças), há a possibilidade
de usar o único momento de inércia na forma I C , também designado I eq .
A forma geral da equação diferencial será (a unidade dos termos envolvidos na equação é a
unidade do momento [Nm ou kNm]):
Ieq  k ,eq  0
em que I eq representa o momento de inércia equivalente de unidade [kgm2 ou tonm2] e k ,eq
é a rigidez rotacional equivalente de unidade [Nm ou kNm]. Após a determinação da equação
de movimento que rege a vibração, basta agrupar os termos para se determinar I eq  0 e
k ,eq  0 (ambos positivos), ou seja, basta juntar os coeficientes das variáveis com a mesma
ordem de derivada de tempo e usar as resoluções pré-calculadas. Visto a equação ter a
mesma forma como anteriormente, basta simplesmente usar I eq no lugar de meq , k ,eq no
lugar de keq e  no lugar de u . As condições iniciais habitualmente designam-se:  0 e  0 , ou
seja não se costuma usar 0 para a velocidade angular inicial para não se confundir com a
frequência circular.
Como já foi dito, durante as vibrações rotacionais cada ponto do sistema faz igualmente a
vibração linear. A transferência faz-se do mesmo modo como se traduziam deslocamentos
infinitesimais para a rotação. Assumindo a posição do ponto na distância d do centro de
rotação, esse ponto efectua o movimento linear u   d . A equação de movimento tem que
se transferir para o equilíbrio de forças, e por isso
u1
 u
 I eq  k ,eq   0
d d
 d
a outra divisão por d transfere o momento para a força, o que seria mais claro se a equação
k ,eq
tivesse o lado direito diferente de zero. Em resumo, para este ponto: keq  2 [N/m ou
d
I eq
kN/m] e meq  2 [kg ou ton]. Realça-se que o valor da frequência circular e do ângulo de
d
fase não se altera, considerando a vibração como rotacional ou como linear. Realça-se ainda
que a equação que rege a vibração é a equação de movimento, no entanto, contrariamente
do capítulo de Dinâmica, tem que se escrever na posição deformada. Verá se mais à frente
que esta exigência é ditada pela introdução correcta das contribuições dos pesos.
Pêndulo
Calcule a frequência circular de um pêndulo simples para as pequenas oscilações.
Resolução
Um pendulo simples está composto pelo fio de
comprimento L de massa desprezável e pela massa
concentrada m de raio desprezável. O movimento
oscilatório representa uma rotação em torno de um
ponto fixo C . Em primeiro lugar admite-se o sentido
positivo de ângulo  e de aceleração angular  .
C
C
 
L
m
IC
L
mg
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Estes sentidos têm que ser iguais, porque está se deduzir uma equação. O momento de inércia
actua como indicado, na tentativa de voltar a estrutura à sua posição de equilíbrio. A
deformada obedece às regras da deformada infinitesimal.
O equilíbrio em torno do ponto C :
IC  mgL  0 , onde IC  mL2
Usando o formulário:
n 
mgL
mgL


IC
mL2
g
L
Nota-se que a equação deduzida não teve nenhum termo absoluto, o que comprova, que não
era necessário escrever primeiro o equilíbrio estático, porque o braço do peso contém apenas
a parte dinâmica. Este problema simples mostra claramente que o equilíbrio era necessário
escrever na posição deformada, se não, a linha de acção do peso passava pelo apoio e o braço
do peso seria nulo.
Problema
Considere novamente o pêndulo mas neste caso não despreze o peso do fio m f e o raio r da
massa concentrada que tem a forma de uma esfera.
Resolução
A resolução segue o mesmo procedimento como no problema anterior. As diferenças são no
momento de inércia
1
2
I C  m f L2  mr 2  mL2
3
5
e na contribuição do peso do fio que actua no centro de massa do fio, ou seja
1
I C  mg  L  r   m f gL  0
2
Usando o formulário:
n 
30mg  L  r   15m f gL
10m f L2  12mr 2  30mL2
Problema
A barra uniforme AB está articulada em C e ligada em A a uma mola de
constante de rigidez k. Assuma que a posição visualizada na figura
corresponde à posição de equilíbrio. Se for imposto à extremidade A um
pequeno deslocamento horizontal e depois libertado, determine:
a) a frequência circular das pequenas oscilações;
b) o menor valor da constante de rigidez kmin para o qual ocorrerão
oscilações.
ku
Resolução
A barra pode fazer movimento de rotação em torno do ponto fixo C,
definindo assim uma vibração rotacional. Introduzindo as forças
 ,
mg
I C
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
actuantes na posição deformada que obedece às regras da deformada
infinitesimal, o equilíbrio dos momentos em torno do apoio dita:
L

IC  ku  d    mgd  0
2

L

Visto que u   d  
2

2
L

I C  k  d    mgd  0
2

Realça-se que a aceleração angular tem que ser introduzida no mesmo sentido como a
rotação, e assim, as forças elásticas actuam contra o movimento introduzido e o momento de
inércia contra a aceleração angular, e por isso as suas contribuições têm o mesmo sinal. A
inércia da estrutura e as forças de restituição das molas actuam no sentido para voltar a
estrutura à sua posição do equilíbrio. No entanto, a contribuição do peso pode ajudar (como
no pêndulo) ou retardar a vibração (como neste problema). Isso depende do facto se o
centro de gravidade (o ponto de actuação do peso) está posicionado abaixo (pêndulo) ou
acima (neste problema) da linha horizontal que passa pelo centro de rotação.
A contribuição da força elástica nas vibrações rotacionais obedece às certas regras. Como o
deslocamento no lugar da mola equivale ao ângulo de rotação vezes a distância deste lugar
ao centro de rotação, e essa mesma distância (braço da força elástica) é depois utilizada no
equilíbrio dos momentos, na equação da vibração vai estar esta distância sempre ao
quadrado.
Concluiu-se que:
2
L

k ,eq  k  d    mgd
2

1
I eq  I C  mL2  md 2
12
a) usando o formulário:
k ,eq
n 
I eq
3k  2d  L   12mgd
2

m  L2  12d 2 
Confirma-se mais uma vez que neste caso o peso reduz a rigidez equivalente, e por isso reduz a
frequência, ou seja aumenta o período, ou seja abranda a vibração.
b) Para que possa ocorrer a vibração, a rigidez equivalente tem que ser positiva, ou seja
2
k ,eq
k
L

 k  d    mgd  0
2

4mgd
 2d  L 
kmin 
2
4mgd
 2d  L 
2
Para rigidezes menores que a mínima, a barra continua a deformar-se depois de ser deslocada.
Isso também significa que a estrutura esteve na sua posição inicial em equilíbrio instável.
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Problema
Considere a estrutura da figura ao lado. Assuma que a
posição representada corresponde à posição do
equilíbrio estático estável.
a) Calcule o deslocamento que a mola sofreu a partir da
sua posição indeformada.
b) Escreva a equação que rege as pequenas vibrações
rotacionais.
c) Escreva a equação que rege as pequenas vibrações
lineares do ponto A.
D
A
Resolução
a) Posição do equilíbrio estável: o deslocamento da mola
que foi necessário introduzir devido à actuação do peso
da estrutura deduz-se na posição deformada, tal como
visualizada na figura, porque esta deformação pode não
ser infinitesimal.
Equilíbrio dos momentos em torno do apoio:
kuest 2a  mB g 2a  mAB g
mD , rD
b
C
mAB
a
k
a
a
mD g
C
mAB g
a
B
mB
mB g
a
a
kuest
4mB  mAB  2mD
a
 mD ga  0 , ou seja, uest  g
2
4k
b) Arbitrando o sentido positivo da rotação, a posição deformada visualiza-se abaixo. Como a
vibração é pequena, esta deformada obedece às regras da deformada infinitesimal.
Equilíbrio dos momentos em torno do apoio:
I C  k  uest  2a  2a  mB g 2a  mAB g
a
 mD g  a  b   0
2

I C
Combinando a equação com o equilíbrio estático, obtém-se:


IC  k  2a   mD gb   0
2
C
 ,
mD g
Realça-se que as forças de inércia a as forças elásticas das
mAB g
molas actuam sempre no sentido de voltar a estrutura à sua
k  uest  u 
posição de equilíbrio. Isso também implica que na equação
a
a
a
da vibração tem que entrar com o mesmo sinal.
Nota-se também que o termo que envolve o momento da força elástica tem sempre o braço
ao quadrado. Isso porque o braço foi utilizado uma vez para representar o deslocamento no
lugar da mola e segunda vez para definir o momento da força elástica.
Os momentos dos pesos cuja actuação está acima (ou abaixo) da recta horizontal que passa
pelo apoio têm uma parte do braço estática e outra dinâmica. A parte estática corta quando
se introduz o equilíbrio estático. A parte dinâmica depende na variável da deformação e por
isso fica na equação que rege a vibração. Esta contribuição reduz (ou aumenta) a rigidez
equivalente da estrutura.
Em resumo, a rigidez equivalente da estrutura é:
k ,eq  k  2a   mD gb
2
E o momento de inércia:
mB g
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
2
1
1
2
2
a
I eq  I C  mAB  3a   mAB    mB  2a   mD rD2  mD  a 2  b 2  
12
2
2
 mAB  4mB  a 2  mD 
1 2

rD  a 2  b 2 
2




Realça-se que a equação IC  k  2a   mD gb   0
2
poder-se-ia obter directamente seguindo a regra que a
equação canónica só pode conter os termos que
envolvam a variável de deformação.
Pode-se assim concluir que todos os pesos que na
estrutura deformada não envolvam no seu braço a
variável de deformação, contribuem apenas para a
posição do equilíbrio estático. Os pesos que
contribuem à vibração têm que ter a sua contribuição
simétrica relativamente à posição do equilíbrio, ou seja
I C
 ,
C
mD g
mB g
k  uest  u 
mAB g
a
a
a
 
o termo mD gb tem que manter o seu efeito na
posição oposta da barra (figura ao lado). Estes pesos
são os pesos que alteram a sua linha de acção mesmo
na deformada infinitesimal.
mD g
mD g
Ou seja juntando as figuras, o movimento da massa mD visualiza-se acima.
Recorda-se que ambos os termos, I eq e k ,eq , na equação canónica têm que ser positivos, ou
seja, k  2a   mD gb . Se a massa mD fosse muito grande após o impulso a estrutura não
2
vibrava, mas continuava a deformar-se. Isso também significa, que a posição inicial era uma
posição de equilíbrio instável, contrariamente ao que foi dito no enunciado.
Os problemas nesta secção permitem concluir que os pesos actuantes acima da linha
horizontal que passa pelo centro de rotação reduzem a rigidez equivalente e por isso
retardam a vibração. Os que estão colocados a abaixo desta linha aumentam a rigidez
equivalente e assim apressam a vibração. Nota-se que este efeito não depende da distância
horizontal do ponto de actuação do peso ao centro de rotação, mas apenas da distância
vertical. Assim a rigidez global da estrutura está inalterada se uma das massas concentradas
for deslocada na direcção horizontal. No entanto, esta alteração afectava o momento de
inércia, ou seja, concentrando as massas destes pesos mais longe do centro de rotação, o
momento de inércia aumenta e a frequência baixa. Concentrando os perto do centro de
rotação, o momento de inércia diminui e a frequência aumenta.
c) A equação deduzida foi:


IC  k  2a   mD gb   0
2
uA  a


uA
u
2
 k  2a   mD gb A  0
a
a
I
b 

Alteração para equilíbrio de forças: C2 u A   4k  mD g 2  u A  0
a
a 

Por isso I C
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
2.2.2 Centro de rotação móvel
Quando o ponto em torno do qual a estrutura está a rodar, mudar a sua posição ao longo da
vibração, com uma pequena alteração, tal como se verifica nos casos em que o centro de
rotação é representado pelo CIR móvel, é possível considerar esta vibração como rotacional e
simplificar a construção da equação que rege o movimento oscilatório como explicado em
seguida. Em primeiro lugar realça-se que as vibrações são consideradas pequenas e por isso
estão descritas por uma equação diferencial linear, o que significa que todos os termos da
equação são formados por um coeficiente multiplicado pela variável ou pela primeira ou
segunda derivada segundo o tempo da variável com expoente 1 (para as vibrações livres nãoamortecidas apenas os termos ~  ou ~  são possíveis, termos de ordem maior como
~  , ~  2 , ~  2 etc. são desprezáveis). Se a alteração da posição do centro de rotação for
descrita via termos pequenos, estes envolveriam a variável  e consequentemente os termos
referentes à inercia e às forças elásticas iriam acrescentar os termos de ordem maior. No
entanto, as partes dos pesos que pertencem às forças de restituição, representam valores sem
dependência da variável, e por isso devem ser utilizados em conjunto com valores que contém
 . Esta análise permite concluir que, os efeitos de inércia e das forças elásticas é possível
escrever na posição indeformada. A contribuição dos pesos pode ser incluída posteriormente
usando o equilíbrio na posição deformada. As componentes normais de aceleração são
definidas em função de  2 que representa o termo de ordem maior. Por esta razão as
respectivas componentes de forças de inércia são desprezáveis, e consequentemente as
componentes de aceleração podem ser determinadas usando os CIRs, semelhante como no
capítulo de Dinâmica no caso das estruturas que iniciam movimento do repouso.
Problema
Uma barra AB de massa mAB e comprimento L está
rebitada a um disco com massa mD e raio r . Uma mola
de constante de rigidez k está ligada ao centro do disco
em A e à parede em C. Sabendo que o disco rola sem
escorregar, determine o período das pequenas
oscilações do sistema.
Resolução
u r
deformada
cinemática
u
a  r


D
forças
I D
kr mD r
2L / 2
r
L / 2
G
Para uma melhor visualização a barra representa-se mais comprida.
Equilíbrio dos momentos em torno do ponto D (CIR na posição nova):
mD g 
Fa
IG
mAB 2 L / 2
N
mAB L / 2
mAB r
mAB g
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
kr 2  I D  mD r 2  I G  mAB gL / 2  mAB r  L cos  / 2  r   mAB L / 2  L / 2  r cos   
3
1
2
mD r 2  mAB L2  mAB  L / 2  r   kr 2  mAB gL / 2  0
2
12
Foram utilizadas as regras de deformada infinitesimal e desprezados termos de ordem maior,
por isso o termo que envolve a contribuição da aceleração normal mAB 2 L / 2 não entrou na
equação, porque contem o termo pequeno ao quadrado e por isso corresponde ao termo de
ordem maior.
Tal como justificado acima, verifica-se que era possível simplificar as deduções da seguinte
maneira.
deformada
indeformada
kr

CIR
D
ICIR
mAB g
Na primeira posição é possível usar o CIR na parte de cinemática para indicar a distribuição
dos deslocamentos e acelerações. Isso permite definir os sentidos e os valores das forças
elásticas e de inércia. O equilíbrio dos momentos em torno do CIR escreve-se na posição
indeformada. Isso não viola nenhum pressuposto, apesar de estar claro que na posição
indeformada a aceleração angular é nula e a contribuição dinâmica da força elástica também,
mas  e  representam funções e não valores, por isso devem verificar a equação que rege a
vibração em qualquer posição, incluído a posição quando o valor da função é nulo. Neste caso
o CIR do conjunto serve como o centro de rotação.
kr 2  ICIR
A segunda posição é deformada. Esta posição é necessária para introduzir correctamente os
efeitos dos pesos, e o equilíbrio escreve-se em torno do CIR na posição nova (no mesmo
sentido como na primeira posição). Esta deformada faz-se como finita, mas os braços são
simplificados usando as normas das deformações infinitesimais ( cos   1 , sin    ). Assim:
mAB gL / 2


Juntando as duas partes: ICIR   kr 2 
1

mAB gL   0
2

em que
2
I CIR 
1
1
3
1
L

L

mD r 2  mD r 2  mAB L2  mAB   r   mD r 2  mAB L2  mAB   r 
2
12
12
2
 2
2

o que confirma o resultado anterior. De acordo com o formulário
n 
k ,eq
I eq

1
kr 2  mAB gL
2
2
3
1
L 
2
2
mD r  mAB L  mAB   r 
2
12
2

2
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Pode se assim concluir que não há significativas diferenças na construção da equação que
rege as pequenas vibrações rotacionais em torno do CIR fixo e móvel. As equações dos
problemas resolvidos no início deste capítulo poder-se-iam obter da mesma maneira. Mas
no caso do CIR fixo não é complicado resolver a equação na posição deformada e por isso
não se justifica esta separação. Mais uma vez realça-se que a separação de contribuições
deve-se ao facto que as forças de inércia e elásticas já envolvem o parâmero da vibração, 
e  , respectivamente, e por isso podem entrar na equação apenas com braços de rotação
definidos pelos parâmetros geométricos sem envolvimento do ângulo de rotação  . Ao
contrário os pesos necessitam o braço dependente da rotação  para contribuir à vibração,
o que exige a posição deformada da estrutura. Excepto dos casos em que o peso representa
única força de restituição, a sua contribuição é geralmente pequena e por isso muitas vezes
desprezada. Nestes casos usa-se apenas a primeira deformada e a resolução torna-se muito
mais simples.
3. Conjuntos de corpos rígidos com movimentos dependentes
Quando são considerados conjuntos de corpos com 1GDL, ou seja corpos com movimentos
dependentes, é vantajoso escrever a equação que rege a vibração usando o PTV, porque isso
permite eliminar directamente as reacções externas do sistema. O trabalho virtual escreve-se
na posição deformada, ou seja, primeiro introduz-se a deformada que corresponde ao
parâmetro de vibração, depois colocam-se as forças actuantes, e em seguida perturba-se esta
deformada com uma deformada virtual. O trabalho virtual tem que ser nulo porque o sistema
de forças aplicadas representa o sistema em equilíbrio a actuar num mecanismo. Recorda-se
que as componentes normais de aceleração são desprezadas, e por isso a inércia de cada
corpo pode ser reduzida ao CIR indiferente do facto de este ser fixo ou móvel.
Problema
Considere a estrutura da figura ao lado composta por
três barras a vibrar com pequenas oscilações. Sabe-se
que a posição mostrada corresponde à posição de
equilíbrio estático. Escreva a equação canónica de
vibração livre.
Resolução
Em primeiro lugar a estrutura separa-se em corpos de
movimentos diferentes e determinam-se os seus CIRs.
Depois traça-se a deformada infinitesimal (azul) em que se
define o parâmetro que vai caracterizar a vibração. Visto a
estrutura ser um mecanismo com 1GDL, a deformada
infinitesimal está caracterizada pelo único parâmetro. No
presente caso escolheu-se o ângulo de rotação  que é
igual para os corpos I e III, corpo II faz translação e a sua
deformação pode ser definida por u   h , e assim, a
vibração pode ser caracterizada pela equação que rege a
vibração rotacional.
m1
m1
h
m2
L
I1,CIR1

I
CIR1
I3,CIR3


III
m1 g
m2 h
II
m2 g
CIR2 , 
CIR3

m1 g
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
No passo seguinte introduzem-se na posição deformada as forças actuantes, neste caso os
pesos e as forças e os momentos de inércia. Para resolver o equilíbrio e não envolver as
reacções externas, usa-se o PTV, ou seja a partir da posição deformada (azul), traça-se a
deformada virtual (vermelha) caracterizada pelo ângulo virtual  . Neste caso as forças de
inércia podem ser simplificadas, tal como explicado no capítulo de Dinâmica. A inércia de cada
corpo pode ser reduzida ao seu CIR, excepto dos corpos em translação.
Ao lado visualiza-se melhor a projecção das forças no corpo II
consoante à deformada virtual. O termo m2 h projectou-se
à direcção da translação com cos   1 . O termo m2 g
projectou-se à direcção da translação com sin    . Em
resumo:
h
2
m2 h h  m2 g h  0
h
2
m2 h

   I1,CIR   m1 g   I 2,CIR   m1 g 
1
2
CIR2 , 

Para o trabalho das forças no corpo II poder-se-iam usar
directamente as componentes do deslocamento virtual, tal
como está explicado na figura ao lado.
A equação final é:
I
1,CIR1

 I 2,CIR2  m2 h 2    m1  m2  gh  0
2
2
2
 m1h  m2 h    m1  m2  gh  0
3

m2 g
h
h
h
m2 h
m2 g
A equação final não revela nenhum termo absoluto, o que significa, que não foi necessário
utilizar o equilíbrio estático.
Realça-se que tal como no problema do CIR móvel, poder-se-iam usar duas posições. Na
primeira, indeformada, actuavam as forças (momentos) de inércia. Pode-se facilmente
verificar, que os termos já obtidos não se alteravam. A segunda posição, deformada, era
somente necessária para contabilizar correctamente os pesos.
Salienta-se que todas as simplificações dever-se-iam justificar a posteriori, ou seja a dedução
da equação que rege a vibração dever-se-ia fazer na posição deformada real (finita). Apenas
depois a equação poder-se-ia simplificar comparando os termos da mesma ordem. Os
termos absolutos representam o equilíbrio estático, os termos lineares regem a vibração
pequena e com o envolvimento de mais termos aumenta-se a precisão da equação que rege
as vibrações o que permite analisar as vibrações grandes. Para as vibrações pequenas
desprezam-se todos os termos de ordem maior que linear. Apenas depois pode-se concluir
que isso significa utilizar a deformada infinitesimal, e por isso as deduções nesta parte da
matéria foram feitas directamente nas deformadas infinitesimais.
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
4. Conservação da energia mecânica
O princípio da conservação da energia mecânica pode ser utilizado para o cálculo da
frequência natural do sistema não amortecido. Visto o valor da energia mecânica ser
constante, admitindo valores positivos para a energia potencial é fácil de justificar que,
quando uma das partes, energia potencial ou cinética é nula, a outra é máxima, e vice-versa.
V1  T1  V2  T2 ou seja 0  Tmax  Vmax  0
A resolução da frequência natural auxilia-se pela propriedade do movimento harmónico que
dita: os extremos de velocidades ocorrem nos instantes de deslocamentos (dinâmicos) nulos
e os extremos de deslocamentos ocorrem nos instantes em que a velocidade é nula. Para a
comparação energética escolhem-se assim estas duas posições extremas, uma que
corresponde à posição nula em que se verifica a velocidade máxima, e outra de deformada
máxima em que a velocidade vira o seu sinal, ou seja é nula. Ainda usa-se que os valores
máximos de deslocamentos e de velocidades correspondem às suas amplitudes e a relação
entre as amplitudes foi identificada na forma:
Av  n Au para a vibração linear e A  n A para a vibração rotacional, ou seja:
umax  numax para a vibração linear e max  nmax para a vibração rotacional,
A primeira posição corresponde à posição do equilíbrio estático estável, é por isso
indeformada, ou seja para as vibrações rotacionais há   0 , para as lineares u  0 , e assim
esta posição pode arbitrar-se como nível zero da energia potencial:
V1  0
Quando a estrutura passa pela posição do equilíbrio, a velocidade atinge o seu máximo, tal
como especificado acima, e por isso a energia cinética é máxima. Por exemplo para 1 corpo em
vibração rotacional verifica-se:
T1 
1
2
I CIR max
2
sendo o CIR fixo ou móvel.
Apenas quando é necessário envolver o equilíbrio estático, por exemplo, para uma correcta
separação da contribuição dos pesos, consideram-se nesta primeira posição as energias
acumuladas nas molas lineares ou rotacionais devido às deformações estáticas, e por isso
podem existir termos por exemplo na forma
V1 
1 2
kuest
2
ou seja a energia potencial pode ser considerada não nula.
A segunda posição é a posição da máxima deformada: para vibrações rotacionais   max ,
para as lineares u  umax . O campo de velocidades é nulo, e por isso T2  0 .
Consequentemente a energia potencial é máxima. Na determinação de V2 é necessário ter
cuidado com a ordem de termos considerados. Visto T1 conter apenas termos quadráticos de
velocidade, a simplificação de funções trigonométricas tem que assegurar que na energia
potencial não há termos absolutos, os termos que representam o equilíbrio estático entram
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
como termos lineares, e os termos que regem as vibrações como termos quadráticos. Para isso
não é suficiente substituir as funções trigonométricas pelo primeiro termo da expansão Taylor,
tal como na deformada infinitesimal, mas as funções de aproximação têm que chegar até aos
termos quadráticos, ou seja:
sin    e cos  1 
2
2
Recorda-se que esta simplificação já foi introduzida no capítulo PTV no cálculo da força crítica.
Nesse contexto os deslocamentos correspondentes foram designados pequenos mas não
infinitesimais.
Na comparação energética a grandeza dos termos é diferente porque não se consideram
forças ou momentos, mas termos energéticos.
Problema
Calcule a frequência circular de um pêndulo simples para as pequenas oscilações. Apresente a
resolução usando o princípio da conservação de energia mecânica.
Resolução
Um pendulo simples está composto pelo fio de
comprimento L de massa desprezável e pela massa
concentrada m de raio desprezável. Para a utilização do
princípio da conservação da energia mecânica é
necessário apresentar a deformada como real (finita) e
apenas depois simplificar as expressões, tal como
explicado acima.
CIR
max
L
V1  0
T1 
1
2
I CIR max
, onde ICIR  mL2
2
posição 1
Única força que faz trabalho para a posição 2 é o peso, o
trabalho é negativo, por isso a energia potencial é
positiva
V2  mgL 1  cosmax 
T2  0
Juntando as expressões
1 2 2
mL  max  mgL 1  cos  max 
2
Simplificando e substituindo cos max  1 
2
  max
1 2 2
Lnmax  g 1  1 
2
2
 
2

max
   g
2

2
max
2
e max  nmax
mg
max
 0
posição 2
mg
max
 0
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
Tal como esperado max corta da equação porque a amplitude do movimento não afecta a
frequência natural. Isso até serve para a verificação do cálculo, pode-se concluir que todos os
2
termos na equação final tem que conter max
. Finalmente:
n 
g
L
o que confirma o resultado anterior.
Problema
Considere novamente o pêndulo mas neste caso não despreze o peso do fio m f e o raio r da
massa concentrada que tem a forma de uma esfera. Calcule a frequência circular. Apresente a
resolução usando o princípio da conservação de energia mecânica.
Resolução
A resolução segue o mesmo procedimento como no problema anterior. As diferenças são no
momento de inércia
1
2
I CIR  m f L2  mr 2  mL2
3
5
e na contribuição do peso do fio que actua no centro de massa do fio, ou seja
V2  mg  L  r 1  cosmax   m f g
2
L
L 2
1  cosmax   mg  L  r  max  m f g max
2
2
2 2
Confirma-se novamente:
n 
30mg  L  r   15m f gL
10m f L2  12mr 2  30mL2
2d 2
Problema
Considere a estrutura da figura ao lado cujo eixo de
simetria corresponde ao eixo vertical que passa pelo
apoio. A massa não desprezável está nas barras inclinadas
(na figura visualizada pela espessura mais grossa) e nos
discos. Admita que as molas encontram-se indeformadas
na posição visualizada e que os discos estão rigidamente
ligados às barras. Calcule a frequência circular. Apresente
a resolução usando o princípio da conservação de energia
mecânica.
h2
mB
h1 / 2
h1 / 2
mD , rD
2d1
mD , rD
mB
k
k
k
Resolução
A primeira posição corresponde à posição visualizada. Nesta posição as molas estão
indeformadas e a velocidade angular é máxima, por isso:
V1  0
T1 
1
2
I CIR max
, onde
2
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
1
  d  d 2  h  h 2  
2
2
I CIR  2  mB  h2  h1    d 2  d1   mB   2 1    2 1   
  2   2  
12


1

2  mD rD2  md  d 22  h22  
2



Antes de representar a segunda posição vale a pena
introduzir
algumas
simplificações.
Uma
simplificação pode ser feita da seguinte maneira: é
possível juntar os corpos simetricamente
posicionados relativamente ao eixo vertical da
estrutura, isso permite que o centro de massa do
conjunto fica colocado no eixo vertical da estrutura
e consequentemente a determinação do trabalho
dos pesos torna-se mais fácil. Também é possível
substituir as molas lineares por uma mola cuja
rigidez equivale a 2k . Depois:
2mD g
2mD g
2mB g
2mB g
2k
k
 h h 

V2  2  mB  2 1  1  cos  max   mD h2 1  cos  max  
  2 

h2 2
1 h
1
 1
h h  2
2
2
2
 2k  1 sin  max   k  max
 mB  2 1   max
 mD h2 max
 k 1  max
 k max
2 2
4
2
 2
 2 
2
Juntando as expressões e substituindo max  nmax :
h2 1
h h 
mB  2 1   mD h2  k 1  k
4 2
 2 
n 
2
  d 2  d1   h2  h1 2  1
1
2
2
2
2
2
mB  h2  h1    d 2  d1   mB  
 
   mD rD  md  d 2  h2 

12
 2   2   2


Problema
Considere a estrutura da figura ao lado composta por
três barras a vibrar com pequenas oscilações. Sabe-se
que a posição mostrada corresponde à posição de
equilíbrio estático. Determine a frequência circular de
vibração pequena usando o princípio da conservação de
energia mecânica.
m1
m1
h
m2
L
Resolução
Em primeiro lugar a estrutura separa-se em corpos de
movimentos diferentes e determinam-se os seus CIRs.
Depois traça-se a deformada infinitesimal (azul) em que se
define o parâmetro que vai caracterizar a vibração. Visto a
estrutura ser um mecanismo com 1GDL, a deformada
infinitesimal está caracterizada pelo único parâmetro.
CIR3
CIR1
max
I
max
m1 g
CIR2 , 
III
II
m2 g
m1 g
Sebenta de Disciplina DCR, Zuzana Dimitrovová, DEC/FCT/UNL, 2016
No presente caso escolheu-se o ângulo de rotação  que é igual para os corpos I e III, corpo II
faz translação e a sua deformação está ligada via u   h .
Posição 1 (cinzenta)
V1  0
T1 


1
2
I1,CIR1  I 2,CIR2  m2 h 2  max
2
Posição 2 (azul)
V2  2m1 g
T2  0
2
2
max
max
h
1

cos


m
gh
1

cos


m
gh

m
gh


max 
2
max 
1
2
2
2
2
Consequentemente
n 
 2m1  3m2  h
3  m1  m2  g
O que confirma o resultado já obtido na secção 3.