Introdução à Análise Estatística com Análise exploratória de dados

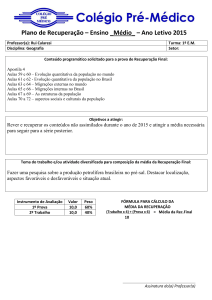
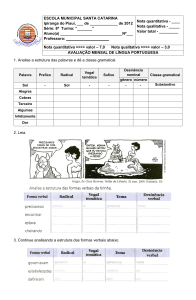
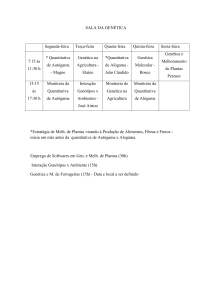
Curso
Análise exploratória de dados univariados
Introdução à Análise Estatística com
População
Unidade Estatística
Variável
Amostra
Objectivo: caracterizar um conjunto de indivíduos, tentando
descobrir regularidades e singularidades
Sessão 3 – Análise exploratória de dados
Notas:
– as conclusões obtidas são apenas válidas para o conjunto de
indivíduos considerados explicitamente no estudo.
Maria João Martins
– os resultados podem usar-se para formular hipóteses sobre a
população, que terão que ser avaliadas posteriormente.
Setembro 2012
Instituto Superior de Agronomia
Grupo de Matemática
2
Natureza dos dados (e respectiva variável)
Dados no R
Qualitativa
V1 V2
– nominal
– ordinal
1
2
...
n
Quantitativa
– discreta
– contínua
...
Vk
n indivíduos
k características
ou variáveis
Data frame com k
componentes de
comprimento n
Cada uma das variáveis vai ser estudada separadamente.
3
4
Variável qualitativa nominal
Representação dos dados
Identificação da natureza da variável
Condensação sob a forma
de tabela de frequências
Dados: Iris (do pacote datasets do R)
Representação gráfica:
diagrama de barras,
histograma, diagrama de
extremos e quartis
Cálculo de indicadores numéricos
de localização, dispersão e forma
> ?iris
> head(iris) #mostra primeiras linhas
> str(iris$Species)
[1] "factor"
– Variável Species é qualitativa nominal.
Tabela de frequências
> ni<-table(iris$Species) #frequencia abs
> fi<-ni/sum(ni)
> cbind(ni,fi)
ni
fi
setosa
50 0.3333333
versicolor 50 0.3333333
virginica 50 0.3333333
5
6
Variável qualitativa nominal
Variável qualitativa ordinal
Indicadores
Dados: Nível de escolaridade mais elevado completo e
sexo da população activa nos Açores (INE, 16 Fev 2011).
Os dados estão armazenados data frame escolar, que se
encontra no workspace “escolaridade.RData”.
– moda (faz sentido para estes dados?)
Representação gráfica – gráfico de barras
– Variável nivel é qualitativa ordinal.
> plot(iris$Species)
> barplot(ni)
> load("escolaridade.RData")
> str(escolar)
> attach(escolar)
> table(nivel)
nivel
N
B1
B2
B3
Sec
5300 30700 28800 22000 18600
#igual ao anterior
7
Sup
13500
8
Variável qualitativa ordinal
Variável qualitativa ordinal
Tabela de frequências
Indicadores de localização
>
>
>
>
média (porquê?)
– quartis, moda, //////////
ni<-table(nivel)
fi<-ni/sum(ni)
Fi<-cumsum(fi)
cbind(ni,fi,Fi)
N
B1
B2
B3
Sec
Sup
ni
5300
30700
28800
22000
18600
13500
fi
0.04457527
0.25820017
0.24222035
0.18502944
0.15643398
0.11354079
> quantile(nivel) #dá erro
Error in quantile.default(nivel) : factors are
not allowed
> quantile(as.numeric(nivel), type=2)
0% 25% 50% 75% 100%
1
2
3
5
6
Fi
0.04457527
0.30277544
0.54499579
0.73002523
0.88645921
1.00000000
> names(ni[ni==max(ni)])
[1] "B1"
#moda
9
Variável qualitativa ordinal
Variável quantitativa
Representação gráfica
– Gráfico de barras
10
Dados: chickwts (do pacote datasets do R)
> barplot(ni)
> head(chickwts)
– Gráficos de barras sobrepostos
Objectivo: comparar o nível de escolaridade por sexo
> table(escolar$sexo,nivel)
nivel
N
B1
B2
B3
Sec
H 4600 21300 18300 12800 8200
M
700 9400 10500 9200 10400
#mostra primeiras linhas
– Variável weight é quantitativa contínua.
Tabela de frequências
– agrupar os dados em classes (quantas? Regra de Sturges)
quando os dados são de natureza contínua ou de natureza
discreta com muitos valores distintos.
Sup
4900
8600
> barplot(table(escolar$sexo,nivel),
beside=T,col=c("blue","pink"))
11
12
Variável quantitativa
Variável quantitativa
Representação gráfica – histograma
> ?hist
> attach(chickwts)
> hist(weight)
#observar simetria e
possivel existencia de duas modas
> hist(weight,plot=F)
#devolve uma lista
breaks – limites das classes
counts – frequência absoluta de cada classe
intensities – (frequência relativa / amplitude) de cada classe
density – idem
mids – ponto médio de cada classe
equidist – lógico que indica se as classes têm ou não amplitude
constante
13
Exercício 1
Nota: se as classes têm amplitude variável, a área de cada
classe deve ser proporcional à frequência (altura
proporcional a frequência/amplitude) – por omissão, no R
> hist(weight,breaks=
c(seq(100,250,50),275,seq(300,450,50)))
#comparar as alturas das classes 3 e 4
> hist(weight,breaks=
c(seq(100,250,50),275,seq(300,450,50)),
freq=T)
#ver mensagem
> hist(weight,prob=T,ylab="Probabilidade")
> lines(density(weight))
#adiciona curva densidade estimada por kernel
14
Variável quantitativa
Fazer a tabela de frequências da variável weight (do
pacote de dados chickwts), usando a lista que resulta
do comando hist com plot=F.
Indicadores de localização: média, média aparada,
mediana, quantis, moda
Exemplos:
> x <- c(0:10, 50)
> mean(x)
[1] 8.75
> mean(x,trim=0.1) #igual a mean(x[2:11])
[1] 5.5
> median(x)
[1] 5.5
> quantile(x)
0%
0.00
25%
2.75
50%
5.50
75% 100%
8.25 50.00
> quantile(x,type=2)
15
0%
0.0
25%
2.5
50%
5.5
75% 100%
8.5 50.0
16
Variável quantitativa
Variável quantitativa
Nota: para dados de natureza contínua ou de natureza
discreta com muitos valores distintos, a moda é dada pela
classe modal ou por um valor da classe modal, calculado
por regras empíricas.
Indicadores de dispersão: variância, desvio padrão,
coeficiente de variação (dispersão relativa), amplitude
total, amplitude inter-quartil, mediana dos desvios
absolutos
Exemplos:
> x <- c(0:10, 50)
> var(x)
#variancia
[1] 178.75
17
Variável quantitativa
> kurtosis(x)
[1] 4.586300
attr(,"method")
[1] "excess"
de achatamento
Necessita do package fBasics
Exemplos:
#coeficiente de achatamento
Observação: é uma medida da concentração da distribuição dos
dados junto ao centro, em comparação com a distribuição
normal.
> x <- c(0:10, 50)
#coeficiente de assimetria
média=mediana=moda
Observação: • simetria:
• assimetria positiva: média>mediana>moda
• assimetria negativa: média<mediana<moda
18
Variável quantitativa
Indicadores de forma: coeficientes de assimetria e
> skewness(x)
[1] 2.384115
attr(,"method")
[1] "moment"
> sd(x)
#desvio padrão
[1] 13.36974
> sd(x)/mean(x) #coeficiente de variacao
[1] 1.527971
> max(x)-min(x) #amplitude total
[1] 50
> IQR(x)
#amplitude inter-quartil
[1] 5.5
> sort(abs(x-median(x)))
[1] 0.5 0.5 1.5 1.5 2.5 2.5 3.5 3.5
4.5 4.5 5.5 44.5
> mad(x)
#igual a median(abs
#(x-median(x)))*constante
[1] 4.4478
• igual a zero:
• positivo:
• negativo:
19
como a normal
mais aguçada do que a normal
menos aguçada do que a normal
20
Variável quantitativa
Variável quantitativa
Resumos de indicadores
x
nobs
12.000000
NAs
0.000000
Minimum
0.000000
Maximum
50.000000
1. Quartile
2.750000
3. Quartile
8.250000
Mean
8.750000
Median
5.500000
Sum
105.000000
SE Mean
3.859512
LCL Mean
0.255271
UCL Mean
17.244729
Variance
178.750000
Stdev
13.369742
Skewness
2.384115
Kurtosis
4.586300
Exemplos:
> summary(x)
Min. 1st Qu.
0.00
2.75
> basicStats(x)
Median
5.50
Mean 3rd Qu.
8.75
8.25
Max.
50.00
#do package fBasics
21
Exercício 2
22
Variável quantitativa
Calcular todos os indicadores referidos para os dados
da variável weight, do pacote de dados
chickwts.
Análise por sub-grupos de dados definidos por factores
> tapply(weight,feed,summary) #feed e' factor
Representação gráfica – diagrama de extremos e quartis
> boxplot(weight, main="Pesos dos frangos",
+ horizontal=T)
Observar que não existem valores atípicos e a distribuição é
simétrica
> x <- c(0:10, 50)
> boxplot(x, horizontal=T) #observar valor
atipico, 50
23
24
Exercício 3
Variável quantitativa
Diagrama de extremos e quartis por sub-grupos de
dados definidos por factores
> boxplot(weight~feed,
main="Pesos dos frangos por dieta")
Relativamente à variável Petal.Width do
conjunto de dados iris (do R), obter para cada
espécie de lírio:
a) tabela de frequências,
A expressão weight~feed é um objecto do tipo formula.
Genericamente, numa fórmula
variavel~expressao
em que variavel representa a variável dependente e
expressao é uma expressão que indica de que
variável(eis) depende variavel. Exemplo: y~x1+x2.
b) histograma,
c) indicadores de localização, dispersão e forma,
d) diagrama de extremos e quartis.
25
Exercício 4
26
Análise exploratória de dados bivariados
Num inquérito realizado a um grupo de alunos,
perguntou-se qual era o número de irmãos que
tinham. Obtiveram-se os seguintes resultados:
Objectivo: evidenciar as relações (eventualmente existentes)
entre variáveis através de indicadores numéricos e
representações gráficas
3, 3, 2, 2, 8, 5, 2, 4, 3, 1, 4, 5, 3, 3, 3, 3, 3, 2, 5
1, 3, 3, 2, 2, 4, 3, 3, 2, 2, 4, 4, 3, 6, 3, 3, 2, 2, 4
3, 4, 3, 2, 2, 4, 4, 3, 3, 4, 2, 5, 4, 1, 2, 8, 2 ,3, 3, 4
a) Represente graficamente este conjunto de dados.
– n observações do par de variáveis (x,y), ou seja n pares de
valores (xi,yi) ,i=1,...,n
– admite-se que ambas as variáveis são quantitativas
b) Calcule a média, a mediana e a moda.
c) Estude a dispersão dos dados.
d) Analise a simetria da distribuição.
27
28
Análise exploratória de dados bivariados
Análise exploratória de dados bivariados
Dados: iris (do pacote datasets do R)
Covariância e coeficiente de correlação
> cov(Petal.Length,Petal.Width)
[1] 1.295609
> cor(Petal.Length,Petal.Width)
[1] 0.9628654
x – largura das pétalas (Petal.Width)
y – comprimento das pétalas (Petal.Length)
Diagrama de dispersão ou nuvem de pontos
> attach(iris)
> plot(Petal.Length~Petal.Width)
> plot(Petal.Width,Petal.Length) #equivalente
Observa-se uma tendência linear positiva relativamente forte.
29
Por omissão cor calcula o coeficiente de correlação usual, de
Pearson. Um indicador mais robusto (menos sensível a
observações atípicas) é o coeficiente de correlação de
Spearman – usa apenas as ordens (e não os valores) das
observações. Pode ser usado em variáveis qualitativas
ordinais.
> cor(Petal.Length,Petal.Width,
+ method="spearman")
[1] 0.9376668
Análise exploratória de dados bivariados
Análise exploratória de dados bivariados
Regressão linear simples
Sobrepor a recta de regressão à nuvem de pontos
Existindo uma correlação linear forte entre x e y, faz sentido
determinar a equação da recta dos mínimos quadrados.
30
> plot(Petal.Length~Petal.Width)
> abline(lm(Petal.Length~Petal.Width))
Em R o modelo linear simples exprime-se através de
lm(y~x) ou lm(y~1+x)
“Matriz” de diagramas de dispersão
> lm(Petal.Length~Petal.Width)
intercept:
ordenada na origem
Petal.Width:
coeficiente associado à variável
Representação das nuvens de pontos para todos os pares de
variáveis
Petal.Width, ou seja o declive da recta.
Equação da recta: y=1.084+2.23x - interpretar!
Para informações sobre a qualidade do modelo:
> plot(iris[-5])
> detach(iris)
> summary(lm(Petal.Length~Petal.Width))
31
32
Exercício 5
O ficheiro
http://knuth.uca.es/repos/ebrcmdr/bases_datos/reproduccion_vir.dat contém
dados relativos ao número de vírus reproduzidos em função do
tempo (minutos), para diferentes tipos de meio de cultura (ácido,
neutro ou básico).
a) Leia o ficheiro para a data frame virus.df.
b) Construa o diagrama de dispersão do número de vírus em
função do tempo, representando os pontos que dizem respeito
aos três tipos de meio com cores diferentes.
c) Calcule os coeficientes de correlação entre as variáveis
“número de vírus” e “tempo” para cada tipo de meio de
cultura. Comente tendo em conta a alínea anterior.
d) Determine os coeficientes da recta de regressão de “número
de vírus” vs. “tempo” para os dados respeitantes ao meio 33
básico. Qual é a precisão da recta de regressão? Interprete.
Bibliografia
The R Manuals, editados por R Development Core Team,
Versão 2.14.1 (Dezembro de 2011)
(http://cran.r-project.org/manuals.html).
“Introdução à Programação em R”, Luis Torgo (Outubro de
2006). Contributed Documentation disponível em
http://cran.r-project.org/other-docs.html.
“Análise Exploratória de Dados”, Bento Murteira, McGraw-
Hill, 1999.
“Introdução à Probabilidade e à Estatística”, Dinis Pestana e
Sílvio Velosa, Fundação Calouste Gulbenkian, 2002.
34