Exemplo: Varivel Aleatria Discreta X(s) = Diferena de pontos no

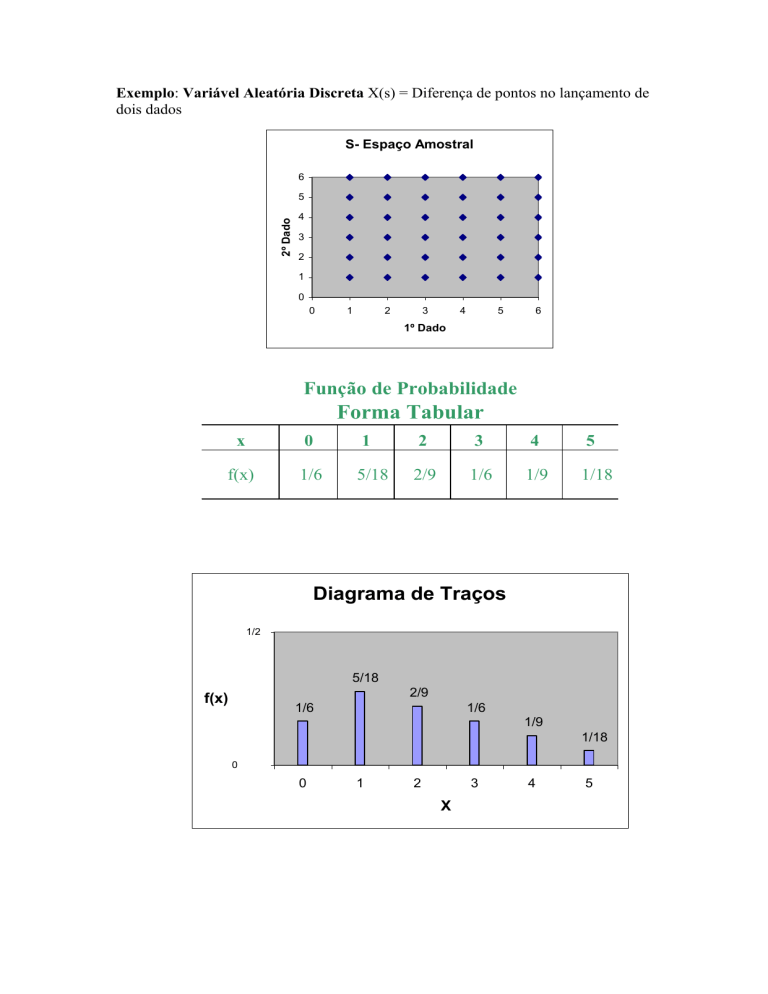
Exemplo: Variável Aleatória Discreta X(s) = Diferença de pontos no lançamento de
dois dados
S- Espaço Amostral
6
2º Dado
5
4
3
2
1
0
0
1
2
3
4
5
6
1º Dado
Função de Probabilidade
Forma Tabular
x
0
1
2
3
4
5
f(x)
1/6
5/18
2/9
1/6
1/9
1/18
Diagrama de Traços
1/2
5/18
2/9
f(x)
1/6
1/6
1/9
1/18
0
0
1
2
3
X
4
5
Função de Distribuição Acumulada F(x):
x<0
⎧0
⎪1
⎪
⎪6
⎪4
⎪
⎪9
⎪2
F ( x) = ⎨
⎪3
⎪5
⎪6
⎪
⎪17
⎪18
⎪1
⎩
0 ≤ x <1
1≤ x < 2
2≤ x<3
3≤ x < 4
4≤ x<5
x≥5
Função de Distribuição Acumulada
Gráfico
F(x)
1
0
0
1
2
3
4
x
5
6
7
8
Exemplo: Variável Aleatória Contínua X(s) = Verdadeiro peso dos sacos de 1Kg de
café da marca “Café”
Função de Densidade de Probabilidade f(x):
0,8 < x < 1,05
outros valores
⎧4
f ( x) = ⎨
⎩0
função densidade probabilidade (f.d.p.)
5
f(x)
4
3
2
1
0
0
0,5
1
1,5
2
x
Função de Distribuição Acumulada F(x):
⎧0
⎪
F ( x) = ⎨4 x − 3,2
⎪1
⎩
x < 0,8
0,8 ≤ x ≤ 1,05
x > 1,05
função de distribuição acumulada
f(x)
1
0
0
0,2
0,4
0,6
0,8
x
1
1,2
1,4
1,6
Exemplo: Distribuição conjunta das variáveis aleatórias discretasX(s)- nº de filhos por família; Y(s): nº de assoalhadas da casa
Função de Probabilidade Conjunta
f XY (x,y)
Y/X
2
3
4
5
0
0.03
0.05
0.02
0
1
0.05
0.1
0.1
0.05
2
0.05
0.15
0.07
0.03
3
0
0.05
0.18
0.02
4
0
0
0.05
0
f Y (y)
f X (x)
Função de Distribuição Acumulada
F XY (x,y)
Y/X
2
3
4
5
F X (x)
0
0.03
0.08
0.1
0.1
1
0.08
0.23
0.35
0.4
2
0.13
0.43
0.62
0.7
3
0.13
0.48
0.85
0.95
4
0.13
0.48
0.9
1
F Y (y)
Funções de Probabilidade Condicional
f XIY (x)
X
fXIY=2(x)
0
3/13
1
5/13
2
5/13
3
0
4
0
fXIY=3(x)
fXIY=4(x)
1/7
1/21
2/7
5/21
3/7
1/6
1/7
3/7
0
5/42
fXIY=5(x)
0
1/2
3/10
1/5
0
Funções de Probabilidade Condicional
f YIX (y)
Y
2
3
4
5
fYIX=0(y)
3/10
1/2
1/5
0
fYIX=1(y)
fYIX=2(y)
fYIX=3(y)
1/6
1/6
0
1/3
1/2
1/5
1/3
7/30
18/25
1/6
1/10
2/25
fYIX=4(y)
0
0
1
0
Exemplo: Distribuição conjunta das variáveis aleatórias contínuasX(s)- Gastos familiares c/ a electricidade; Y(s): Gastos familiares c/ os
transportes. (unidade -10€)
Função de densidade de probabilidade conjunta:
⎧1 2 2
⎪ x y
f XY ( x, y ) = ⎨81
⎪⎩0
0 ≤ x ≤ 3, 0 ≤ y ≤ 3
o.v.
Função de distribuição acumulada conjunta:
⎧ x y1 2 2
⎪∫0 ∫0 u v dudv
FXY ( x, y ) = ⎨ 81
⎪⎩0
0 ≤ x ≤ 3, 0 ≤ y ≤ 3
Função de densidade de probabilidade marginal de X:
⎧1 2
⎪ x
f X ( x) = ⎨ 9
⎪⎩0
0≤x≤3
o.v.
Função de densidade de probabilidade marginal de Y:
⎧1 2
⎪ y
fY ( y) = ⎨9
⎪⎩0
0≤y≤3
o.v.
o.v.
Função de distribuição acumulada marginal de X:
⎧ x1 2
⎪∫0 u du
FX ( x) = ⎨ 9
⎪⎩0
0≤x≤3
o.v.
Função de distribuição acumulada marginal de Y:
⎧ y1 2
⎪∫0 v dv
FY ( y ) = ⎨ 9
⎪⎩0
0≤y≤3
o.v.
Função de probabilidade condicional de X/Y:
⎧1 2
⎪ x dx
f X / Y = y ( x) = ⎨9
⎪⎩0
0≤x≤3
o.v.
Função de probabilidade condicional de Y/X:
⎧1 2
⎪ y dy
f Y / X = x ( y ) = ⎨9
⎪⎩0
0≤y≤3
o.v.