Cronograma e Guia de Física 1a – 1o Semestre de 2010 Olá

o
Cronograma e Guia de Física 1a – 1 Semestre de 2010
Olá, parabéns!
Parabéns por pertencer a este consórcio que envolve algumas das melhores universidades do Brasil. Parabéns por
ter chegado até aqui, em física 1 a, depois de passar um concurso vestibular e pelas disciplinas introdutórias.
Nesta disciplina, física 1 a, e na seguinte, física 1 b, estudaremos a física clássica, mais especificamente, a mecânica .
Nos cursos tradicionais, esta é a primeira disciplina de física que os alunos da área de exatas (física, matemática,
química, engenharia, ..) estudam em nível universitário.
Eu sou o coordenador de física 1 a e meu nome é Antônio Carlos . Estaremos em contato virtual ao longo deste
bimestre ou semestre. Já que agora você me conhece um pouco, deixe-me conhecer um pouco de você também.
Eu inicialmente gostaria de saber qual o motivo que fez você escolher o CEDERJ, dentre tantas opções de
universidades públicas e privadas. Você escolheu porque busca um ensino de qualidade e gratuito ? você escolheu
porque acredita que só através do ensino de qualidade podemos mudar os índices que apontam que nossos jovens
têm um dos piores desempenhos acadêmicos do mundo, principalmente em matemática ? você escolheu o CEDERJ
por discordar da prática que algumas instituições adotam em forçar o professor a distribuir boas notas a alunos com
baixo desempenho apenas para que não os percam para outras instituições onde é mais fácil passar ? Você não se
conforma com o sistema de ensino predominante, onde professores mal preparados `ensinam’conceitos errados a
alunos que jamais conseguirão ascender socialmente, alimentando um circulo vicioso e covarde? Você acredita que
para resolver as distorções sociais do nosso país, precisamos dar uma educação de qualidade a toda a população e
não somente aos mais privilegiados? Se você respondeu a sim a todas as questões acima, você esta no lugar certo!
Bem, agora que já nos conhecemos um ao outro um pouco mais, vou tecer alguns comentários que têm por
objetivo tentar responder a algumas questões que os alunos nos indagam. Em primeiro lugar, você já percebeu que
ensino à distância não significa ensino de baixa qualidade, mais fácil ou ‘mole’ de passar. Na verdade, como você já
deve ter percebido, este curso é mais difícil do que o curso presencial, pois exige maturidade e organização por
parte dos alunos. Além do fato de não ter o professor ao lado.
Isto leva a alguns alunos a se sentirem desorientados e perdidos. Muitos nos acusam de descaso, de não nos
preocuparmos com o seu baixo rendimento. É claro que ficamos muito tristes com estas acusações injustas. Mas,
isto faz parte do oficio de professor. Vocês também serão...
Então, gostaríamos de mostrar que não estão sozinhos. O sucesso dos alunos é nosso sucesso também, assim como
o fracasso do aluno e nosso fracasso também. As instituições não investiriam tanto tempo, dinheiro e pessoal para
deixá-los desamparados. Há um verdadeiro exército de pessoas que aqui estão para ajudá-lo. São tutores
presenciais e a distância, diretores de pólo, coordenadores, secretárias, pessoal de apoio logístico, enfim, muita
gente que faz este consórcio funcionar. E ainda tem mais, você não precisar pagar nada! É tudo gratuito! Mas já
dizia um grande economista: ‘não existe jantar gratuito’ . Há sempre um preço a ser pago. No nosso caso, o preço
que cobramos de você é o empenho, a dedicação e o ‘suor` . Me parece justo, voce não acha?
Dicas de como estudar e aprender realmente física
1
Nós professores e tutores estamos interessados em ajudar você a aprender. Desejamos a você um bom
aproveitamento nesta disciplina. O objetivo deste material complementar é fornecer algumas idéias que podem
ajudar você a ter êxito em física 1a . O alto índice de reprovação nas disciplinas iniciais de física não é uma
particularidade do CEDERJ, é um fenômeno mundial. Veja, por exemplo, o comentário de Peduzzi e colaboradores,
que pesquisam há anos os problemas enfrentados por alunos:
“ O elevado índice de reprovação e a falta de motivação para o estudo de física, em nível universitário básico, tem
sido motivo de constante preocupação por parte de professores, estudantes e administradores não só de nossa
Universidade, como de todas as Instituições de Ensino Superior do pais com conteúdos de Física em seus currículos.
O aluno recém egresso do segundo grau, sujeito em geral a um ensino de qualidade bastante discutível, acaba
esbarrando, nas primeiras disciplinas que lhe são oferecidas, com exigências muito superiores às que normalmente
encontra-se preparado. Nesse sentido, é sem dúvida na Mecânica, usualmente introduzida como primeiro tópico de
Física em disciplinas de Física Geral para os cursos de Física, Engenharia, Matemática, Química, etc.., onde mais se
acentuam esses problemas. O aluno, até então sem hábito de leitura, da reflexão individual, passa a ser pressionado
pelo professor para buscar em livros de texto o complemento indispensável aos assuntos abordados em sala de
aula. ...É justamente na resolução de problemas em Física, onde se espera que o aluno, de forma significativa e não
mecânica, relacione idéias e opere com os conceitos e princípios que aprendeu, que muitas dificuldades, não
apenas de ordem conceitual, vêm a tona. A não compreensão, em níveis desejáveis, dos temas abordados e
insuficientes conhecimentos matemáticos sintetizam, para muitos, os fatores responsáveis pelos maiores
insucessos nesta área da aprendizagem... De fato, muitos alunos, mesmo dispondo de um razoável conhecimento
de um dado assunto, mal lêem o enunciado de um problema e já se consideram incapazes de encaminhar a sua
solução . Não tentam, sequer, dar inicio ao mesmo. Outros, sem uma adequada fundamentação teórica, aplicam,
cegamente, equações que não se ajustam à situação tratada.”
Peduzzi et al. Revista Brasileira de Ensino de Física vol 14, 239 (1992)
Aprendendo a aprender
Muitos alunos reclamam que estudam, estudam e não conseguem ter um bom desempenho nas avaliações. Mas
como é exatamente este estudo? Quantas horas se dedicam diariamente? Será que estão estudando corretamente?
Daremos algumas dicas de como estudar. O importante é ser honesto consigo mesmo e responder às seguintes
perguntas:
a) Me sinto preparado para usar os conceitos matemáticos de álgebra,geométrica e cálculo ? Caso sinta
dificuldades com a matemática, procure o tutor de seu pólo e peca um programa de revisão;
b) Eu li o material do módulo ? entendi os conceitos apresentados ? fiz os exercícios propostos? Alguns
alunos reclamam que o texto e muito longo e gostariam de um material mais resumido. Devemos
entender que não aprendemos os conceitos fundamentais em resumos com as “fórmulas” . Mais
importante do que a fórmula, é o conceito implícito. O material do módulo foi pensado pelos autores de
modo a suprir a ausência de aulas presenciais, por isto e tão longo. Nosso diagnóstico é que grande parte
do alunato sente dificuldades na parte conceitual, muito mais do que na matemática.
c) Eu dedico um tempo adequado aos meus estudos de física? Uma regra pratica e que você dedique ao
mínimo quatro horas de estudo para cada aula do módulo. Em uma semana, você deve dedicar pelo
menos 12 horas para esta disciplina. Você pode estar indagando: Ora, mas eu não tenho este tempo!
Infelizmente, temos que fazer escolhas na vida. Para ser bem sucedido, não só em física 1, mas na vida, e
necessário que sejamos organizados e disciplinados. Ninguém prometeu a você que seria fácil! Não e fácil,
mas também não e impossível. Nós professores, tutores e ex-alunos também passamos por isto. Lembrese, se vem fácil, vai fácil. Tudo que tem valor exige muita dedicação. Vivemos no mundo do fast food, do
rápido, do agora. Mas isto não vale para as coisas que tem valor. Nos cursos presenciais, os alunos têm
cerca de seis horas semanais de aula e normalmente recomendamos que para cada hora de aula, o aluno
estude individualmente mais três horas.
d) Eu estudo em ambiente silencioso para manter a minha atenção focalizada?
Note que é de extrema importância que a ênfase no estudo seja dada a assimilação dos conceitos. A maior das
dificuldades encontrada pelos alunos do curso de Física 1 é o vício de estudar exclusivamente por exercícios e
gabaritos de avaliações anteriores. Esse hábito vem, em geral, do Ensino Médio mas não funciona nos cursos de
Física do Ensino Superior. O objetivo de qualquer disciplina de um curso de Ensino Superior deve ser o aprendizado
dos conceitos apresentados e a resolução de exercícios deve ser uma consequência desse aprendizado. Os Módulos
do CEDERJ são divididos em Aulas para guiar o estudo. No início de cada aula estão especificados os objetivos da
mesma. Portanto, o aluno deve estudar o conteúdo de uma determinada Aula, depois disso, ele deve voltar e ler
novamente os Objetivos para verificar se eles foram atingidos. Se não tiverem sido, ele deve procurar novamente a
parte que não ficou clara e, persistindo a dúvida, entrar em contato com os tutores a distância para tentar
solucionar os problemas. Note que as tutorias presenciais não devem se transformar em aulas expositivas. Até
2
porque não há como uma tutoria por semana substituir 3 aulas de 2 horas existentes no curso presencial. Somente
depois de ter estudado é que o aluno deve tentar fazer os exercícios propostos. Outro fator que causa dificuldade é
o hábito de somente se olhar a resolução dos gabaritos sem tentar resolver os exercícios. O gabarito só deve servir
para o aluno verificar se o exercício está correto ou, em alguns casos, ter uma idéia de qual o procedimento
utilizado.
Erros comuns que os novatos cometem;
Não estude pelos gabaritos. Só recorra aos gabaritos depois de tentar sozinho resolver o problema. Busque a sua
solução! Não conseguiu resolver? Não busque ainda o gabarito. Por que não conseguiu? Não entendeu os
conceitos? Não entendi o enunciado? É importante tentar várias vezes. Se mesmo assim não conseguiu, organize
um grupo de estudos, troque informações com seus colegas. A última opção é recorrer ao gabarito.
Alguns alunos frequentemente nos questionam sobre os exercícios programados, EP. Nossa opinião sobre o assunto
é a seguinte: Os alunos devem sempre procurar resolver exercícios como forma de verificação do aprendizado, se
os conceitos foram bem entendidos e são aplicados corretamente. As questões nas quais os alunos são avaliados
nas AP`s , exigem não somente a mera repetição da teoria, mas a aplicação criativa destes conhecimentos. Neste
sentido, o direcionamento, ou treinamento em apenas um tipo de exercício, leva a memorização de sua solução e
não ao aprendizado dos conceitos. Por exemplo, quando aplicamos questões muito parecidas em diferentes
avaliações, verificamos que o aluno responde igual ao gabarito da anterior, muito embora as questões não sejam
idênticas. Ou seja, memorizaram a solução; não entenderam!
A divisão das aulas é tão somente para o aluno ter uma idéia do ritmo do curso. Pequenas alteracões podem ser
feitas. O importante é que a matéria das AP’s de Física 1a vai até a aula 20.
A pedido do Cederj tivemos que escolher as datas das AD’s de forma que haja tempo hábil para que as mesmas
sejam corrigidas e eventualmente discutidas pelos alunos com os tutores presenciais antes das respectivas AP’s
Datas importantes:
• AD1:
– Data (máxima) de divulgação - 7/03
– Data de devolução pelos alunos nos pólos - 27/03
• Data da AP1 - 18/04
• AD2:
– Data (máxima) de divulgação - 09/05
– Data de devolução pelos alunos nos pólos - 29/05
• Data da AP2 - 13/06
• Data da AP3 - 4/7
Obs. Será permitido o uso de calculadora e régua nas AP’s de Fisica 1 A.
Alguns alunos pediram que sugeríssemos uma rotina de estudo. Segue uma programação que inclui 12 horas
semanais de estudo individual. Neste roteiro, sugerimos 4 horas de estudo por aula. Em algumas aulas, você poderá
levar menos tempo, como por exemplo na aula 1. Em outras, você poderá ter mais dificuldade, e
consequentemente, levar mais tempo. Nestas 4 horas, estão incluídos o tempo para leitura cuidadosa do módulo e
o tempo para resolução de problemas. Mas, como no CEDERJ o aluno tem a liberdade de escolher o seu ritmo, cada
um pode criar o seu próprio roteiro de estudo. O mais importante é a disciplina e organização.
Avaliação
O critério de avaliação consiste em 20% de uma avaliação a distância (AD) e 80 % de uma avaliação presencial (AP).
Por ser uma disciplina bimestral, o aluno pode ser aprovado ou não nas notas parciais (N1). Em todas as disciplinas
bimestrais da física, o aluno está inscrito no início do semestre em 2 delas. Digamos, como exemplo, que esteja
inscrito em Física 1A e em Física 1B. Ele vai fazer somente a AD1 e a AP1 de Física 1A. Com isso, será calculada a
média ponderada N1=(80×AP1+20×AD1)/ 100 . Existem 3 possibilidades:
1. Se N1 ≥ 6 o aluno está aprovado em Física 1 A e deve fazer o curso de Física 1B no segundo bimestre (AD2 e
AP2).
2. Se N1 < 3, a inscrição em Física 1B será automaticamente trancada e o aluno deverá repetir 1A no segundo
bimestre (AD2 e AP2).
3. Se 3 ≤ N1 < 6, em princípio será repetido o procedimento para o caso 2) e essa é a nossa sugestão. Porém, se o
aluno julgar que aprendeu o conteúdo e só não foi aprovado por um descuido, pode tentar fazer física 1B no
3
segundo bimestre. Para isso, ele deve comunicar o seu tutor presencial logo após a divulgação da N1. Isso deve ser
feito para que a sua inscrição em Física 1B não seja trancada. Se assim optar, ele deverá fazer a AD2 e AP2 somente
de Física 1B, deixando para tentar a aprovação em Física 1A na AP3. Mas insisto que somente em alguns casos
específicos isso deve ser feito por o índice histórico de aprovação dos alunos que assim fazem é baixíssimo. Se o
aluno não for aprovado nem com N1, nem com N2, deverá fazer a AP3 que será sua nota final. Se a nota na AP3
(NAP3) for ≥ 5, o aluno estará aprovado. Para ser aprovado também é necessário que o aluno tenha feito as
práticas obrigatórias. Caso contrário será reprovado por falta. Se o aluno realizou as práticas nos dois semestres
anteriores ao atual (e somente nesse caso), estará dispensado de repetir as práticas.
Tutores
Por ser um curso semipresencial, o CEDERJ exige dos alunos uma iniciativamuito maior do que os cursos presenciais.
A ausência de aulas expositivas cria a necessidade de os alunos procurarem ajuda por conta própria. Além de poder
criar grupos de estudo (o que é fortemente desejável) os alunos tem os tutores, presenciais e a distância para
ajudá-los. Os tutores presenciais são responsáveis pelas práticas e as tutorias ocorrem cerca de 1 vez por semana.
Para que as dúvidas não se acumulem é absolutamente necessárioque quando encontre alguma dificuldade, seja na
teoria ou na resolução de exercícios,o aluno procure os tutores a distância. Os tutores a distância atendem no
telefone 08002823939 e o horário de atendimento encontra-se disponível na Plataforma do CEDERJ (na seção
Informações Acadêmicas) e na Sala de Tutoria da mesma Plataforma (http://www.cederj.edu.br).
Estratégia para resolução de problemas
1-leia cuidadosamente o enunciado anotando as informações (dados do problema) e o que está sendo pedido
(variável alvo do problema, ou seja, a grandeza que se está tentando descobrir : força, velocidade da partícula,
aceleração, etc...) . Se preciso leia mais de uma vez. Leitura e interpretação do texto é uma etapa fundamental para
a resolução de problemas e é onde grande parte dos alunos têm dificuldade;
2- anote as informações (dados do problema)
3-Faça um esboço da situação (faça um desenho)
4-identifique os conceitos relevantes (leis de Newton, leis de conservação, etc...). Esta etapa não envolve cálculo,
mas é onde os alunos têm maior dificuldade;
5-preparar o problema: com base na informação que se deseja obter e nos conceitos envolvidos, escolha as
equações que usará par a resolver o problema e defina como vai usá-las (por exemplo: se vai projetar os vetores em
eixos x e y, etc..)
6- executar a solução: neste passo, entra a matemática. Nesta fase, a parte mais difícil já foi superada (itens 1-5),
mas há a necessidade de bons conhecimentos de álgebra e trigonometria;
7-avaliar a resposta: a resposta obtida faz sentido? É coerente? Se a o objetivo era obter o g da Terra e você
2
encontra 0,02 m/s , algo deu errado.
Importante! Muitos alunos estudam pelos gabaritos das AD’s e AP’s de semestres anteriores. Esta prática não é
recomendável. Observamos que os alunos memorizam a solução sem entendê-la . Tente resolver o problema sem
olhar para o gabarito. Teve dificuldades? Tente de novo. Por quê não conseguiu? Não fixou os conceitos? Então leia
o módulo de novo. Ainda não consegue? Forme um grupo de estudo com seus colegas e tentem resolver juntos.
Ainda não conseguem? Procure os tutores locais ou à distância, pelo 0800 ou pela plataforma. Mas lembrem-se, os
tutores são orientados a não dar a resposta mastigada. Eles deverão mostrar o caminho. É o aluno que deve
resolver sozinho o problema. Olhar gabarito deve ser a última opção.
Roteiro de estudo (sugerido)
Semana 1
Aula 1- Noções básicas sobre o movimento (4 horas)
Aula 2 – A descrição matemática do movimento (4 horas)
Aula 3 –Deslocamento e velocidade média do movimento (4 horas)
Semana 2
Aula 4 – velocidade instantanea no movimento retilíneo (4 horas)
Aula 5 –de volta às funções-movimento (4 horas)
Aula 6 – gráficos do movimento (4 horas)
Semana 3
4
Aula 7 – aceleração no movimento retilíneo (4 horas)
Aula 8 – movimentos não-retilineos e vetores (4 horas)
Aula 9 – cinemática vetorial (4 horas)
Semana 4
Aula 10 – começando a praticar (4 horas)
Aula 11 – exemplos de movimentos não-retilíneos (4 horas)
Aula 12 – medindo o movimento (de acordo com a programação do pólo)
Aula 13 – partícula isolada, referencial inercial e forças (4 horas)
Semana 5
Aula 14 – conceito de massa inercial e a segunda Lei de Newton (4 horas)
Aula 15 – princípio da superposição e Terceira Lei de Newton (4 horas)
Aula 16 – O problema fundamental da Mecânica Clássica (4 horas)
Semana 6
Aula 17 – Translação de um corpo rígido (4 horas)
Aula 18 – Forças elásticas – forças dadas e forças vinculares (4 horas)
Aula 19 – Aplicação das leis de Newton (4 horas)
Semana 7
Aula 20 – E Newton tinha razão... (de acordo com a programação do pólo)
Revisão – exercícios de revisão (12 horas)
Exercícios adicionais.
Estes exercícios complementam os exercícios do módulo, além das AD’s e AP’s dos semestres anteriores. O nível de
dificuldade está indicado. A cada semestre, novos exercícios são adicionados. Sugestão : faça preferencialmente
todos os exercícios propostos no módulo e, só então, faça os exercícios adicionais abaixo. Caso deseje, há uma
bibliografia no final com mais exercícios.
Aula 1- Noções básicas sobre o movimento
Aula 2 – A descrição matemática do movimento
Aula 3 –Deslocamento e velocidade média do movimento
3.1 – (médio) Um ciclista move-se sobre uma estrada retilínea e horizontal, com uma velocidade de 8,0 km/h,
dirigindo-se para uma torre cujo vértice está situado a uma altura de 60 m acima de seus olhos. Calcular a
velocidade com a qual o ciclista vê o vértice da torre se aproximando, no instante em que ele esta a 80 m da base
da torre.
Aula 4 – velocidade instantânea no movimento retilíneo
2
4.1 – (fácil) Considere uma partícula descrevendo um movimento descrito por x(t) = 2 + 3t – t , onde x(t) é a posição
da partícula dada em metros e t em segundos. A) qual a posição da partícula em t = 0 s? b) calcule a velocidade da
partícula em função do tempo;
Aula 5 –de volta às funções-movimento
Aula 6 – gráficos do movimento
Aula 7 – aceleração no movimento retilíneo
7.1 – (fácil) Considere o movimento unidimensional de uma partícula sujeita a uma força. A função-movimento da
2
3
partícula é dada por: x (t) = a - bt+ct +dt onde a, b,c e d são constantes reais e positivas.
a) Escreva as função-velocidade e a função-aceleração da partícula.
b) Esboce os gráficos da posição, velocidade e aceleração da partícula em função do tempo.
7.2- O gráfico abaixo mostra a aceleração de um corpo em função do tempo. Faça um gráfico, em papel
milimetrado, da velocidade em função do tempo e um da posição em função do tempo, sabendo que o corpo parte
da origem em t = 0 com velocidade nula.
5
7.3- Considere o movimento unidimensional de uma partícula sujeita a uma força. A função-movimento da
2
3
partícula é dada por: x (t) = a - bt+ct +dt , onde a, b,c e d são constantes reais e positivas.
a- Escreva as função-velocidade e a função-aceleração da partícula.
b- Esboce os gráficos da posição, velocidade e aceleração da partícula em função do tempo.
Aula 8 – movimentos não-retilineos e vetores
Aula 9 – cinemática vetorial
9.1 – (médio) Um time de futebol americano registra as suas jogadas usando deslocamentos de vetores, sendo a
origem a posição da bola no momento do inicio da partida. Em um certo passe, o recebedor parte de 1,0i-5,0j, onde
as unidades são em metros, i aponta para a direitae j para baixo no campo. Deslocamentos subseqüentes do
recebedor são 9,0i, 11.0j, -6,0i+4,0j, e 12,0i+18j. Enquanto isto, o arremessador recua para uma posição -7,0j. A que
distância e em que direção deve o arremessador passar a bola?
9.2 - A velocidade da corrente de um rio é de 10 km/h. Um barco a motor, ao atravessar o rio chegou à margem
oposta em um ponto x = 250 m abaixo do ponto oposto ao da partida. Sabendo-se que durante toda a travessia a
velocidade própria do barco (velocidade em relação à corrente do rio) foi mantida constante e igual a 5 km/h,
dirigida sempre perpendicularmente à corrente do rio, calcular o tempo gasto pelo barco na travessia. Calcule
também a largura do rio.
9.3 - Um rio corre para norte com velocidade v1 = 3,0 km/h uy.Um barco segue para leste com a velocidade de v2 =
4,0 km/h ux relativa à água.
a- Calcular a velocidade do barco relativa à terra.
b- Sendo a largura do rio 1,0 km, calcular o tempo necessário para atravessá-lo;
c- Que desvio para norte terá sofrido o barco ao atingir a outra margem?
d- Qual deveria ser a orientação do barco (ângulo em relação à direção leste), para que ao atravessar o
rio de uma margem à outra, chegasse a um ponto diametralmente oposto?
9.4 - Uma partícula de massa m= 5 kg move-se em uma direção arbitrária no espaço em relação a um referencial
OXYZ . No instante to = 0 s, a partícula encontrava-se na posição ro = (2ux +3uy -5uz) m com uma velocidade vo = (-2
ux + 5 uy) m/s, quando uma força vertical dirigida no sentido negativo do eixo y constante de módulo 5 N é aplicada
até o instante t = 10 s.
a) Determine a posição da partícula em função do tempo.
b) Determine a velocidade da partícula em função do tempo.
Calcule o ângulo que o vetor velocidade da partícula faz com a direção horizontal (eixo x) no instante t = 2 s
2
9.5 - A função-velocidade de uma partícula que se move no espaço OXYZ é dada por v= 2 ux + 3t uy + (5t +2) uz no
Sistema de Internacional de unidades. Calcule:
a- A função-movimento, sabendo que no instante t = 0 s a partícula passava pela origem.
b- A função-aceleração da partícula.
c- O ângulo entre o vetor-posição e a velocidade no instante t = 1 s.
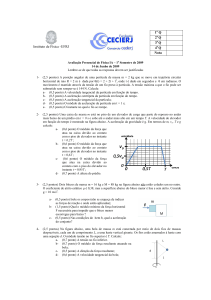
9.6 - Um caminhão trafega ao longo de uma estrada em linha reta (tomada como sendo o eixo x) com velocidade v
= vux . Um atirador dispara um projétil de massa desprezível, com velocidade de módulo |v’| = v’ em direção ao
caminhão. O projétil atravessa a lona do caminhão, de modo que ambos os buracos de entrada (ponto P na Figura
1) e saída (ponto P’ na Figura 1) do projétil estão diametralmente opostos. Suponha que o projétil não seja defletido
ao atravessar a caixa, mas que sua velocidade seja reduzida a 0,8v’.
a-
bc-
Calcule o ângulo com que o projétil foi disparado
em relação à estrada (ângulo entre os vetores v e
v’).
Calcule a velocidade relativa do projétil em
relação ao automóvel antes de atingi-lo.
Se a caixa possui uma largura l, calcule o
deslocamento do automóvel enquanto o projétil
atravessa a caixa.
6
Aula 10 – começando a praticar
Aula 11 – exemplos de movimentos não-retilíneos
11.1- (fácil) Uma pedra é lançada a partir de uma altura de 3,0 m acima do solo. Um gráfico estroboscópico da
posição da bola é mostrado na figura abaixo, onde as leituras são realizadas em um intervalo de 0,45 s e a pedra é
lançada em t = 0.
a- Qual a velocidade inicial da pedra?
b- Qual a velocidade da pedra no instante sua altura máxima?
c- Qual a altura máxima?
d- Qual é o alcance da pedra?
10
Y(m)
8
6
4
2
0
0
20
40
60
X(m)
11.2 - (médio) A) Mostre que, para um projétil lançado num ângulo φo acima da horizontal, em relação a um
terreno plano, a razão da altura máxima para o alcance R é dada por H/R = tgφo /4
B) Encontre o ângulo de lançamento para o qual a altura máxima e o alcance horizontal são iguais.
11.3 - Um corpo é lançado verticalmente de baixo para cima com uma velocidade inicial de 80 m/s e 2s após deixase cair um corpo de um ponto situado a 320 m verticalmente acima do ponto de lançamento do primeiro corpo.
2
Supondo g = 10 m/s , calcular a altura, acima do ponto de lançamento, os dois corpos se encontrarão.
11.4- (médio) Calcular a duração da queda de um corpo, sabendo-se que ele caiu sem velocidade inicial e que
percorreu no último segundo de movimento um espaço igual à terça parte da altura total da queda. Considere g =
2
10 m/s .
11.5- (médio)Um corpo é lançado verticalmente de baixo para cima com uma velocidade inicial vo. Depois de um
intervalo de tempo T um outro corpo é lançado do mesmo ponto e nas mesmas condições. Calcular :
a) A razão v1/v2 entre as velocidades dos dois corpos no momento do encontro;
b) quanto tempo após o lançamento do primeiro corpo se dará o encontro?
c) a que distância do ponto de lançamento se dará o encontro
11.6 - Um disco de raio r = 2 m gira com movimento uniforme de 15 rad/s. No instante t = 5 s, a posição angular de
um ponto situado na periferia do disco era θ = π .
a) Obtenha θ em função do tempo t.
b) Calcule o período T, e a freqüência f, do movimento.
o
c) Quanto tempo leva o disco para girar de um ângulo de 780 ?
d) Calcule a velocidade do ponto.
e) Calcule a aceleração centrípeta do ponto.
7
11.7 - Uma pedra é arremessada até um muro de altura h com velocidade inicial de 42,0 m/s fazendo um ângulo θo
o
= 60,0 com a horizontal, conforme mostra a figura. A pedra atinge o ponto A, 5,5 s após o lançamento .
o
1/2
o
Dados: sen 60 = 3 /2 e cos 60 = ½ .a- Encontre a altura h do muro; b- A velocidade da pedra no logo antes
do impacto em A;c- A altura máxima H alcançada pela pedra.
11.8 - Uma partícula descreve um movimento circular uniforme. No instante t1 = 2,0 s, a velocidade da partícula é v1
= (3,0 x + 4,0 y) m/s, medida em um sistema de coordenadas xy. No instante t2 = 5,0 s, a velocidade da
partícula é v2 = (-3,0 x – 4,0 y) m/s. Calcule:a) A aceleração centrípeta da partícula;b)A aceleração média entre
os instantes t1 e t2;
Aula 12 – medindo o movimento
12.1 – (trabalhoso) Faça a análise dos dados que você obteve na prática “ O movimento do carrinho sobre o trilho
de ar” .
Aula 13 – partícula isolada, referencial inercial e forças
13.1 – (fácil) enuncie a primeira lei de Newton (fácil porém poucos acertaram na AP)
Aula 14 – conceito de massa inercial e a segunda Lei de Newton
14.1 – (fácil) o que é massa inercial?
14.2 –(fácil) enuncie a segunda lei de Newton (fácil porém poucos acertaram na AP)
Aula 15 – princípio da superposição e Terceira Lei de Newton
15.1 – (fácil) enuncie a terceira lei de Newton (fácil porém poucos acertaram na AP)
15.2 – (fácil) Comente a seguinte afirmação: “Um cavalo puxa uma carroça. A carroça puxa o cavalo com uma força
igual e de sentido oposto. A resultante destas duas forças opostas é nula; assim sendo, não pode haver movimento.´´
(fácil porém poucos acertaram na AP)
Aula 16 – O problema fundamental da Mecânica Clássica
Aula 17 – Translação de um corpo rígido
17.1 – (fácil) uma partícula de massa m1 = 1,0 kg encontra-se na posição x1 = 2,0 m e uma segunda partícula de
massa m2 = 3,0 kg encontra-se na posição x2= - 3,0 m. Sem fazer nenhuma conta, você seria capaz de dizer se o
centro de massa do sistema encontra-se mais próximo da partícula 1 ou da partícula 2? Agora, calcule a posição do
centro de massa do sistema.
Aula 18 – Forças elásticas – forças dadas e forças vinculares
-1
18.1-(médio) Um bloco de massa m está em repouso sobre uma rampa inclinada de um ângulo θ = arctg (µe), onde
µe é o coeficiente de atrito estático entre a superfície da rampa e o bloco. Portanto, o bloco está na iminência de
entrar em movimento. Perturba-se ligeiramente o bloco, de modo que ele comece a descer a rampa com um
movimento uniformemente acelerado. Sendo µc o coeficiente de atrito cinético entre as superfícies em contato,
calcule o módulo da aceleração do bloco em termos de g, µc e µe.
-1
18.2- (médio) Um bloco de massa m está em repouso sobre uma rampa inclinada de um ângulo θ = arctg (µe), onde
µe é o coeficiente de atrito estático entre a superfície da rampa e o bloco. Portanto, o bloco está na iminência de
entrar em movimento. Perturba-se ligeiramente o bloco, de modo que ele comece a descer a rampa com um
movimento uniformemente acelerado. Sendo µc o coeficiente de atrito cinético entre as superfícies em contato,
calcule o módulo da aceleração do bloco em termos de g, µc e µe.
18.3-Bagagem é transportada de um ponto a outro em um aeroporto por uma esteira. Em certo ponto, a esteira
o
move-se para baixo fazendo um ângulo de 2,5 com a horizontal. Suponha que não há deslizamento da bagagem
para ângulos tão pequenos quanto este. Determine o módulo da força de atrito da esteira sobre uma caixa de
pesando 69 N nos casos em que a caixa está na parte inclinada da esteira e que a velocidade da esteira é : (a) nula ;
2
(b) 0,65 m/s e constante; (c) 0,65 m/s e aumenta a uma taxa de 0,20 m/s ; (d) 0,65 m/s e diminui a uma taxa de
2
2
0,20 m/s ; (e) 0,65 m/s e aumentando a uma taxa de 0,57 m/s ; (f) em quais destas situações a força de atrito está
2
apontando para baixo na direção da inclinação? (considere g = 10 m/s )
18.4 – (médio) Considere duas rampas inclinadas, perpendiculares entre si, e que formam com o solo um triângulo
retângulo, como ilustra a figura abaixo. Dois blocos idênticos de massa m estão, inicialmente em repouso nos
pontos mais altos de cada rampa. A rampa menos inclinada, a da direita na figura, forma um ângulo θ com a
8
horizontal e, nela o atrito é desprezível. Em contrapartida, o coeficiente de atrito cinético entre a rampa da
esquerda e o bloco que desliza sobre ela é µc. Verifica-se então, que os blocos deslizam sobre as rampas.
a- Supondo que ambos os blocos iniciem seus movimentos de descida no mesmo instante e que atinjam o
solo simultaneamente, determine o coeficiente de atrito µc. Expresse sua resposta em termos de θ.
b- Interprete o resultado do item anterior para θ = π/4.
18.5 - Uma caixa de 1,5 kg está inicialmente em repouso em um superfície horizontal quando em t = 0 uma força
horizontal F = (1,8t) x (com t em segundos e F e Newtons) é aplicada na caixa. A aceleração da caixa em função do
2
tempo é expressa como : a = 0 para 0 ≤ t ≤ 2,8 s e a = (1,2 t – 2,4) x m/s para t > 2,8 s.
a- Qual o coeficiente de atrito estático entre a caixa e a superfície ?
b- Qual o coeficiente de atrito cinético entre a caixa e a superfície ?
18.6 - Um trem de brinquedo, de massa m, se move em um trilho em movimento circular uniforme vertical de raio
R, conforme ilustra a Figura 2. O módulo da força normal de contacto entre o trilho e o trem no ponto A vale 3 mg.
abc-
Calcule a velocidade do trem.
Calcule o módulo da força normal nos pontos B, C e D
indicando o seu sentido.
Se o módulo da normal no ponto A fosse 3mg/2, qual
seria o novo valor e sentido da normal no ponto C ?
18.7 - Na figura abaixo, um bloco de massa m = 5,0 kg desliza para cima no plano inclinado fazendo um ângulo θ =
o
30 com a horizontal, sob a ação de uma força horizontal F = 50 N. O coeficiente de atrito cinético entre o bloco e o
2
o
o
plano é de µ = 0,30. Considerando g = 10 m/s e lembrando que sen(30) = ½ e cos(30 ) = 3 ,
2
ab-
c-
Calcule o módulo e determine a direção e o sentido
da aceleração do bloco.
Se o bloco é arremessado para cima com velocidade
inicial de 4,0 m/s, qual a distância que ele desliza até
parar.
Supondo que o coeficiente de atrito estático seja µe
= 0,31, o que acontece com o bloco quando atinge o
ponto mais alto?
18.8 - A posição angular de uma partícula de massa m = 2 kg que se move em trajetória circular horizontal de raio R
2
= 2 m é dada por θ(t) = 2 + 2t + t , onde t é dado em segundos e θ em radianos. O movimento é mantido
através da tensão de um fio preso à partícula. A tensão máxima a que o fio pode ser submetido sem romper-se
é 144 N. Calcule:a) A velocidade tangencial da partícula em função do tempo.b)A aceleração centrípeta da
partícula em função do tempo.c) A aceleração tangencial da partícula;d) O módulo da aceleração da partícula
em t = 1 s;e) O instante no qual o fio se rompe.
18.9- Na figura abaixo, uma bola de massa m está conectada por meio de dois fios de massas desprezíveis, cada um
de comprimento L, a uma haste vertical girante. Os fios estão amarrados à haste com uma sepação d. O módulo
tensão no fio superior é T. Calcule:
9
abcd-
A tensão no fio inferior.
O módulo da força resultante atuando na bola;
A direção da força resultante;
A velocidade tangencial da bola;
Aula 19 – Aplicação das leis de Newton
19.1 – (fácil) Se você está agachado (como quando está olhando os livros na prateleira de baixo de uma estante) e
se levanta repentinamente, você pode sentir uma tontura momentânea. Como as leis de Newton explicam isso?
19.2 – (médio) Um elevador carregado possui massa total de 2200 kg. Os cabos muito desgastados, podem suportar
uma tensão máxima de 28000 N. a) Faça um diagrama de força do corpo livre para o elevador. Em termos das forças
que atuam no seu diagrama, qual é a força resultante sobre o elevador? Aplique a segunda lei de Newton para o
elevador e ache a aceleração máxima de baixo para cima para o elevador, sem que os cabos se rompam.b) Qual
2
seria a resposta para o item (a) se o elevador estivesse na Lua, onde g = 1,62 m/s .
19.3- A figura abaixo mostra bloco de 4,4 kg (bloco A ) e um bloco de 2,6 kg (bloco B). Os coeficientes de atrito
estático e atrito cinético entre o bloco A e a mesa são 0,18 e 0,15 respectivamente. A) Determine a massa mínima
do bloco C que deve ser colocado sobre o bloco A para impedi-lo de deslizar. B) o bloco C é repentinamente
retirado de cima de A. Qual é a aceleração de A? Considere a roldana sem massa.
19.4- Encontre a força F necessária para manter em equilíbrio, em termos de P, no caso mostrado abaixo. Despreze
as massas das polias.
10
19.5 – (médio) Considere a figura abaixo. O coeficiente de atrito cinético entre o bloco de massa m1 e o piso é µ e o
fio é inextensível. Em termos de F, θ, µ, m1 e m2, calcule:
ab-
a aceleração dos corpos;
a tensão no fio;
19.6 – (médio) Um escovão de massa m é empurrado com uma força F dirigida ao longo do cabo, que faz um ângulo
θ com a vertical. O coeficiente de atrito cinético com o solo é µ.
a- Desenhe um diagrama mostrando todas as forças que agem sobre o escovão;
b- Para θ e µ dados, determine a força F necessária para que o escovão deslize com velocidade
uniforme sobre o assoalho;
19.7 - Uma caixa de massa m está no piso de um elevador de carga que parte do repouso no andar mais baixo de
um prédio em t = 0 s e sobe até o andar mais alto em um tempo T. A velocidade do elevador em função do tempo é
mostrado na figura abaixo. A aceleração da gravidade é g. Em termos de m, vo, T e g calcule:
a- O módulo da força que atua na caixa
devido ao contato com o piso do
elevador no instante t = 0,2T ;
b- O módulo da força que atua na caixa
devido ao contato com o piso do
elevador no instante t = 0,6T ;
c- O módulo da força que atua na caixa
devido ao contato com o piso do
elevador no instante t = 0,95T ;
d- A altura do prédio.
19.8- Dois blocos de massa m = 16 kg e M = 88 kg na figura abaixo não estão colados um no outro. O coeficiente de
2
atrito estático µ é 0,38, mas a superfície abaixo do bloco maior é lisa e sem atrito. Conside g = 10 m/s .
ab-
c-
Isole os corpos (não se esqueça de indicar as forças de
reação e onde estão aplicadas);
Qual o módulo mínimo da força horizontal F
necessária para impedir que o bloco menor
escorregue para baixo ?
Nas condições do item b, qual a aceleração do
conjunto?
Aula 20 – E Newton tinha razão...
20.1 – (trabalhoso) Faça a análise dos dados que você obteve na prática “E Newton tinha razão...” .
Referências adicionais (devem ser utilizados com fonte de exercícios)
[1] Fundamentos da Física I, Halliday, Resnick e Walker, diversas edições
[2] Física Vol. I, Halliday, Resnick
[3] Física, P. A. Tipler, vol. 1
[4] Física Básica 1, Moysés Nussenzveig
[5] Física I , Young e Freedman (Sears & Zemansky), Pearson Education
11