em dúvida nenhuma energia é o termo técnico, originário da Física

Trabalho
Para se colocar algum objeto em movimento, é necessária a aplicação de uma força e, simultaneamente, uma
transformação de energia. Quando há a aplicação de uma força e um deslocamento do ponto de aplicação
dessa força, pode-se dizer que houve uma realização de trabalho.
Note que, para realizar-se um trabalho, existe a necessidade de um deslocamento. Caso algum objeto esteja
sob a ação de uma força, mas em repouso, não haverá a realização de trabalho. As forças que atuam sobre
uma pessoa parada segurando uma mala não realizam
trabalho pois não há deslocamento do ponto de aplicação dessas forças.
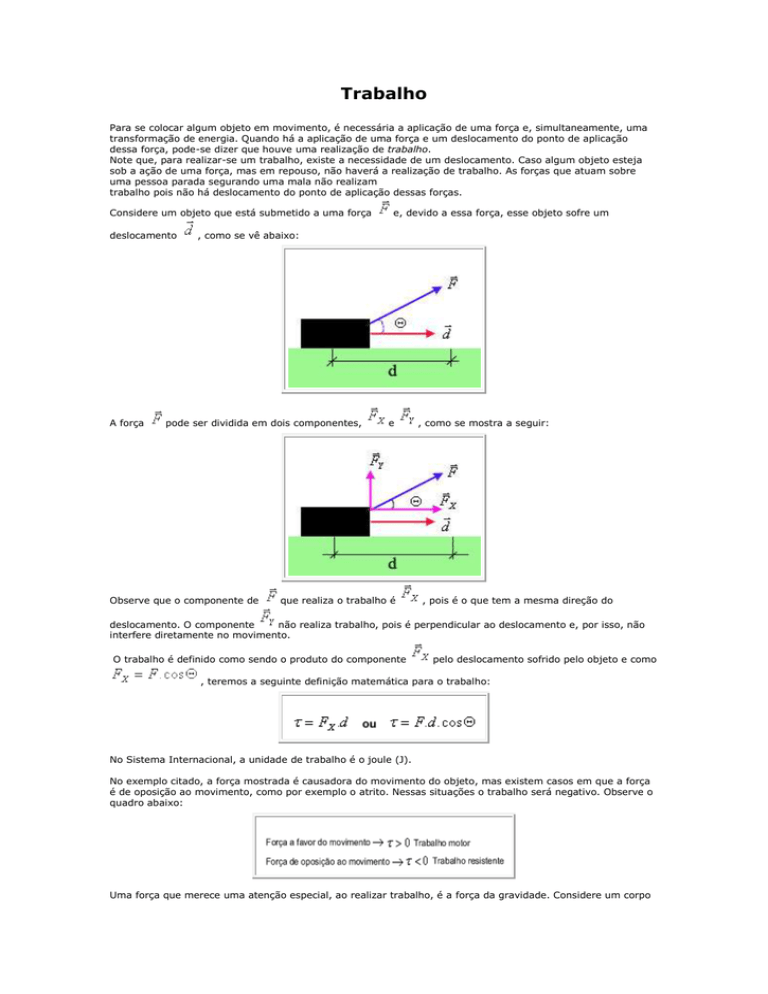
Considere um objeto que está submetido a uma força
deslocamento
A força
e, devido a essa força, esse objeto sofre um
, como se vê abaixo:
pode ser dividida em dois componentes,
Observe que o componente de
e
que realiza o trabalho é
, como se mostra a seguir:
, pois é o que tem a mesma direção do
deslocamento. O componente
não realiza trabalho, pois é perpendicular ao deslocamento e, por isso, não
interfere diretamente no movimento.
O trabalho é definido como sendo o produto do componente
pelo deslocamento sofrido pelo objeto e como
, teremos a seguinte definição matemática para o trabalho:
No Sistema Internacional, a unidade de trabalho é o joule (J).
No exemplo citado, a força mostrada é causadora do movimento do objeto, mas existem casos em que a força
é de oposição ao movimento, como por exemplo o atrito. Nessas situações o trabalho será negativo. Observe o
quadro abaixo:
Uma força que merece uma atenção especial, ao realizar trabalho, é a força da gravidade. Considere um corpo
que é abandonado de certa altura. Durante o movimento de queda temos um deslocamento para baixo e uma
força, a gravidade, que também é direcionada para baixo. Sabemos que, se há uma força e um deslocamento
do ponto de aplicação, haverá a realização de trabalho. Nesse caso o trabalho será determinado pelo produto
da força da gravidade pela altura de queda do objeto:
É importante salientar que o trabalho da força da gravidade independe da trajetória descrita durante o
movimento e por isso ela é classificada como força conservativa.
A força da gravidade também é conhecida como força peso que é constante quando se está próximo da
superfície da Terra e é calculada com o produto da massa do objeto pela a aceleração da gravidade local.
Em uma descida, o trabalho da força da gravidade é positivo, pois ela está contribuindo com o movimento,
mas, em uma subida, o trabalho da força da gravidade será negativo, pois agora ela é de oposição ao
movimento.
é o vetor que indica deslocamento.
ENERGIA MECÂNICA
em dúvida nenhuma energia é o termo técnico, originário da Física, mais empregado em
nossa vida cotidiana.
Energia é um conceito muito abrangente e, por isso mesmo, muito abstrato e difícil de ser
definido com poucas palavras de um modo preciso. Usando apenas a experiência do
nosso cotidiano, poderíamos conceituar energia como “algo que é capaz de originar
mudanças no mundo”. A queda de uma folha. A correnteza de um rio. A rachadura em uma parede. O
vôo de um inseto. A remoção de uma colina. A construção de uma represa. Em todos esses casos, e em
uma infinidade de outros que você pode imaginar, a interveniência da energia é um requisito comum.
Muitos livros definem energia como “capacidade de realizar trabalho”. Mas esta é uma definição
limitada a uma área restrita: a Mecânica. Um conceito mais completo de energia deve incluir outras áreas
(calor, luz, eletricidade, por exemplo). À medida que procuramos abranger áreas da Física no conceito de
energia, avolumam-se as dificuldades para se encontrar uma definição concisa e geral.
Mais fácil é descrever aspectos que se relacionam à energia e que, individualmente e como um
todo, nos ajudam a ter uma compreensão cada vez melhor do seu significado.
Vejamos, a seguir, alguns aspectos básicos para a compreensão do conceito de energia.
S
1) A quantidade que chamamos energia pode ocorrer em diversas formas. Energia pode ser
transformada, ou convertida, de uma forma em outra (conversão de energia).
Exemplo:
A energia mecânica de uma queda d’água é convertida em energia elétrica a qual, por exemplo,
é utilizada para estabilizar a temperatura de um aquário (conversão em calor) aumentando, com isso, a
energia interna do sistema em relação à que teria à temperatura ambiente. As moléculas do meio, por sua
vez, recebem do aquário energia que causa um aumento em sua energia cinética de rotação e translação.
2) Cada corpo e igualmente cada “sistema” de corpos contém energia. Energia pode ser transferida de
um sistema para outro (transferência de energia).
Exemplo:
Um sistema massa/mola é mantido em repouso com a mola distendida. Nestas condições, ele
armazena energia potencial. Quando o sistema é solto, ele oscila durante um determinado tempo mas
acaba parando. A energia mecânica que o sistema possuía inicialmente acaba transferida para o meio
que o circunda (ar) na forma de um aumento da energia cinética de translação e rotação das moléculas
do ar.
3) Quando energia é transferida de um sistema para outro, ou quando ela é convertida de uma forma em
outra, a quantidade de energia não muda (conservação de energia).
Exemplo:
A energia cinética de um automóvel que pára é igual à soma das diversas formas de energia nas
quais ela se converte durante o acionamento do sistema de freios que detém o carro por atrito nas rodas.
4) Na conversão, a energia pode transformar-se em energia de menor qualidade, não aproveitável para o
consumo. Por isso, há necessidade de produção de energia apesar da lei de conservação. Dizemos que
a energia se degrada (degradação de energia).
Exemplo:
Em nenhum dos três exemplos anteriores, a energia pode “refluir” e assumir sua condição inicial.
Nunca se viu automóvel arrancar reutilizando a energia convertida devido ao acionamento dos freios
quando parou. Ela se degradou. Daí resulta a necessidade de produção constante (e crescente) de
energia.
Considerações Gerais
C
hamamos de Energia Mecânica a todas as formas de energia relacionadas com o
movimento de corpos ou com a capacidade de colocá-los em movimento ou deformá-los.
Classes de energia mecânica
1) Energia potencial
É a que tem um corpo que, em virtude de sua posição ou estado, é capaz de realizar trabalho. [3]
Podemos classificar a energia potencial em:
a) Energia Potencial Gravitacional (EPG)
Está relacionada com a posição que um corpo ocupa no campo gravitacional terrestre e sua
capacidade de vir a realizar trabalho mecânico.
Matematicamente
Ou, sabendo que P = m.g,
Exercícios resolvidos:
1) Um corpo de massa 4 kg encontra-se a uma altura de 16 m do solo. Admitindo o solo como nível de
referência e supondo g = 10 m/s2, calcular sua energia potencial gravitacional.
Resolução:


2) Um corpo de massa 40 kg tem energia potencial gravitacional de 800J em relação ao solo. Dado g = 10
m/s2 , calcule a que altura se encontra do solo.
Resolução:



b) Energia Potencial Elástica (EPE)
É a energia armazenada em uma mola comprimida ou distendida.
Matematicamente
Exercícios resolvidos:
3) Uma mola de constante elástica k = 400 N/m é comprimida de 5 cm. Determinar a sua energia
potencial elástica.
Resolução:


4) Qual é a distensão de uma mola de constante elástica k = 100 N/m e que está armazenando uma
energia potencial elástica de 2J?
Resolução:



2) Energia Cinética (EC)
Todo corpo em movimento possui uma energia associada a esse movimento que pode vir a
realizar um trabalho (em uma colisão por exemplo). A essa energia damos o nome de energia cinética.
Matematicamente
Exercícios resolvidos:
5) Determine a energia cinética de um móvel de massa 50 kg e velocidade 20 m/s.
Resolução:


ma força é chamada conservativa, quando pode devolver o trabalho realizado para
vencê-la. Desse modo, o peso de um corpo e a força elástica são exemplos desse tipo de
força. No entanto, a força de atrito cinético, que não pode devolver o trabalho realizado
para vencê-la, é uma força não-conservativa, ou dissipativa (ocorre degradação da
energia mecânica).
Isso quer dizer que, em um sistema no qual só atuam forças conservativas
(sistema conservativo), a ENERGIA MECÂNICA (E M) se conserva, isto é, mantém-se com
o mesmo valor em qualquer momento, mas alternando-se nas suas formas cinética e potencial
(gravitacional ou elástica).
U
Exercícios resolvidos:
6) Uma esfera de massa 5 kg é abandonada de uma altura de 45m num local onde g = 10 m/s 2. Calcular
a velocidade do corpo ao atingir o solo. Despreze os efeitos do ar.
Resolução:
Desprezando a resistência do ar, o sistema é conservativo, logo:


7) Um corpo de 2 kg é empurrado contra uma mola de constante elástica 500 N/m, comprimindo-a 20 cm.
Ele é libertado e a mola o projeta ao longo de uma superfície lisa e horizontal que termina numa rampa
inclinada conforme indica a figura. Dado g = 10 m/s 2 e desprezando todas as formas de atrito, calcular a
altura máxima atingida pelo corpo na rampa.
Resolução:
Como o sistema é conservativo, temos:

8) Um esquiador de massa 60 kg desliza de uma encosta, partindo do repouso, de uma altura de 50 m.
Sabendo que sua velocidade ao chegar no fim da encosta é de 20 m/s, calcule a perda de energia
mecânica devido ao atrito. Adote g = 10 m/s2.
Resolução:
Exercícios propostos:
1) Um garoto abandona uma pedra de massa 20 g do Resolução:
alto de um viaduto de 5 m de altura em relação ao solo.
Considerando g = 10 m/s2 , determine a velocidade e a
energia cinética da pedra ao atingir o solo. (Despreze os
efeitos do ar.)
2) Um corpo de massa 0,5 kg é lançado, do solo, Resolução:
verticalmente para cima com velocidade de 12 m/s.
Desprezando a resistência do ar e adotando g = 10 m/s2,
calcule a altura máxima, em relação ao solo, que o corpo
alcança.
3) Um pêndulo de
massa 1 kg é levado
a posição horizontal
e
então
abandonado.
Resolução:
Sabendo que o fio tem um comprimento de 0,8 m e g =
10 m/s2, calcule a velocidade do pêndulo quando passar
pela posição de altura mínima.
4) Do alto de uma torre de 61,6 n de altura, lança-se Resolução:
verticalmente para baixo, um corpo com velocidade de 8
m/s. Calcule a velocidade com que o corpo atinge o solo.
Adote g = 10 m/s2 e despreze os efeitos do ar.
5) Um corpo de massa 2 kg é lançado do solo, Resolução:
verticalmente para cima, com velocidade de 50 m/s.
Sabendo que, devido ao atrito com o ar, o corpo dissipa
100 J de energia sob a forma de calor, determine a altura
máxima atingida pelo corpo. Adote g = 10 m/s 2.
6) Um corpo de massa igual a 0,5 kg e velocidade Resolução:
constante de 10 m/s choca-se com uma mola de
constante elástica 800n/s. Desprezando os atritos,
calcule a máxima deformação sofrida pela. mola.
7) Consideremos uma mola de constante elástica 400 Resolução:
N/m, e um corpo de massa 1 kg nela encostado que
produz uma compressão de 0,8 m. Liberando a mola,
qual é a velocidade do corpo no instante em que perde
contato com ela? Despreze as forças de resistência.
8) No escorregador
mostrado na figura,
uma criança com 30
kg
de
massa,
partindo do repouso
em A, desliza até B.
Resolução:
Desprezando as perdas de energia e admitindo g = 10
m/s2, calcule a velocidade da criança ao chegar a B.
9) Um corpo de massa m é empurrado contra uma mola Resolução:
cuja constante elástica é 600 N/s, comprimindo-a 30 cm.
Ele é liberado e a mola o projeta ao longo de uma
superfície sem atrito que termina numa rampa inclinada
conforme a figura. Sabendo que a altura máxima atingida
pelo corpo na rampa é de 0,9 m e g = 10 m/s 2, calcule m.
(Despreze as forças resistivas.)
10) Um corpo de
massa 20 kg está
sobre uma mola
comprimida de 40
cm. Solta-se a mola
e deseja-se que o
corpo atinja a altura
de 10 m em relação
à sua posição inicial.
Resolução:
Determine a constante elástica da mola. Adote g = 10
m/s2 e despreze os efeitos do ar.
11) Uma esfera parte do repouso em A e percorre o Resolução:
caminho representado sem nenhum atrito ou resistência.
Determine sua velocidade no ponto B.
12) Um carrinho situado no ponto (veja a figura), parte do Resolução:
repouso e alcança o ponto B.
a)
Calcule a velocidade do carrinho em B, sabendo
que 50% de sua energia mecânica inicial é dissipada
pelo atrito no trajeto.
b) Qual foi o trabalho do atrito entre A e B?
13) Uma esfera de massa 2 kg é lançada Resolução:
horizontalmente do ponto A e deseja-se que ela atinja a
pista superior. Os trechos AB e BCD são perfeitamente
lisos. A aceleração da gravidade é de 10 m/s 2. Determine
a mínima velocidade que o corpo deve ter ao atingir o
ponto B.
14) Uma esfera é suspensa por um fio ideal. Quando Resolução:
abandonada da posição A sem velocidade inicial, ela
passa por B com velocidade de 10 m/s. Desprezando as
resistências, determine o valor da altura h, de onde a
esfera foi solta. Adote g = 10 m/s2.
1) 10 m/s
2) 7,2 m/s
3) 4 m/s
4) 36 m/s
5) 120 m
6) 0,25 m
7) 1,6 m/s
8) 8 m/s
9) 3 kg
10) 25 N/m
11) 10 m/s
12)
e –20J
13) 10 m/s
14) 5 m
Lista de exercícios
Trabalho, Potencia e Energia
Pense um Pouco!
*) Que trabalho realizamos sobre um corpo que é levantado a uma
determinada altura? Esse trabalho seria positivo ou negativo?
**) Se você pudesse segurar um elefante a uma determinada altura, você
estaria realizando trabalho? Por quê?
***) Um menino puxa um carrinho sem rodas, por um barbante.
Há algum trabalho sendo realizado sobre o carrinho? Por quê? O trabalho é
positivo ou negativo.
O menino desenvolve alguma potência? Por quê?
O carrinho tem energia cinética? Por quê?
1) (UNIRIO)
Três corpos idênticos de massa M deslocam-se entre dois níveis, como
mostra a figura: A - caindo livremente; B - deslizando ao longo de um
tobogã e C - descendo uma rampa, sendo, em todos os
movimentos, desprezíveis as forças dissipativas. Com relação ao trabalho
(W) realizado pela força-peso dos corpos, pode-se afirmar que:
a) WC > WB > WA
b) WC > WB = WA
c) WC = WB > WA
d) WC = WB = WA
e) WC < WB > WA
2) (UMC-SP) Sobre trabalho, potência e energia, pode-se afirmar que:
a) potência e energia são sinônimos.
b) trabalho e potência se expressam com a mesma unidade.
c) para trabalho e energia usa-se a mesma unidade.
d) potência é a capacidade de realizar trabalho.
e) trabalho é a relação energia-tempo.
f) para trabalho e energia usa-se a mesma unidade.
3) (UFSE) Um corpo está sendo arrastado por uma superfície horizontal com
atrito, em movimento uniforme. Considere as afirmações a seguir:
I. O trabalho da força de atrito é nulo.
II. O trabalho da força peso é nulo.
III. A força resultante que arrasta o corpo é nula.
Dentre as afirmações:
a) É correta a I, somente.
b) É correta a II, somente.
c) É correta a III, somente.
d) São incorretas I, II, III.
e) São corretas II e III.
4) (UFRS) Um menino puxa uma caixa com velocidade constante, sobre um piso
horizontal, vencendo uma força de atrito, também constante. Sobre essa situação são
feitas as seguintes afirmações:
I. O trabalho que o menino realiza é diferente de zero.
II. O trabalho realizado pela força peso sobre a caixa é zero.
III. O trabalho realizado pelo menino é igual, em módulo, ao trabalho realizado pela
força de atrito.
Quais estão corretas?
a) Apenas I
b) Apenas III
c) Apenas I e II
d) Apenas II e III
e) I, II e III
5) Um operário eleva lentamente uma carga de massa igual a 40 Kg à altura de 10 m,
gastando 20s nessa operação. Sendo g = 10 m/s² e desprezando as massas da corda
e da polia, bem como o atrito na polia, o trabalho realizado pela força que o operário
aplica e a potência útil são, respectivamente:
a) 400 J e 200 W
b) 200 J e 400 W
c) 400 J e 400 W
d) 200 J e 4,0 kw
e) 4,0 Kj e 200 W
6) Uma força de 300N realiza um trabalho de 700 J, no deslocamento de um objeto.
Calcule o valor desse deslocamento.
7) Sobre o trabalho de uma força, podemos afirmar que:
a) é diretamente proporcional à força
deslocamento.
aplicada e inversamente proporcional ao
b) é diretamente proporcional à força e ao deslocamento.
c) não depende do deslocamento.
d) não depende da força aplicada.
e) só depende do deslocamento.
8) Uma força realiza trabalho de 20 J, atuando sobre um corpo na mesma direção e no
sentido do seu deslocamento. Calcule a intensidade da força aplicada para um
deslocamento de 5 m.
9) Uma força de 200 N é utilizada para empurrar uma mesa de uma distância de 3 m.
Calcule o valor do trabalho dessa força.
10) Uma força realiza um trabalho de 100 J desenvolvendo uma potencia de 20 W
Calcule o intervalo de tempo para a realização desse trabalho.
11) Uma força de 300 N realiza um Trabalho de 800 J em 10 s. Calcule a potência
dessa força.
12) Uma partícula de 3kg move-se com velocidade de 10 m/s. Calcule sua energia
cinética.
13) (UFPE 2003) Um garoto desliza sobre um escorregador, sem atrito, de 5,0 m de
altura. O garoto é lançado em uma piscina e entra em contato com a água a uma
distância horizontal de 2,0 m, em relação à borda. Calcule a distância vertical h, entre
a superfície da água e a borda da piscina. Dê sua resposta em cm.
14) (UFPE 2006) Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso
no ponto A, é largado de uma altura h = 1,6 m. O bloco desliza, sem atrito, ao longo de
uma superfície e colide, no ponto B, com uma mola de constante elástica k = 100 N/m.
Determine a compressão máxima da mola, em cm.
15) (UNICAMP 2005) Num conjunto arco e flecha, a energia potencial elástica é
transformada em energia cinética da flecha durante o lançamento. A força da corda
sobre a flecha é proporcional ao deslocamento x, como ilustrado na figura.
a) Quando a corda é solta, o deslocamento é x = 0,6 m e a força é de 300 N. Qual a
energia potencial elástica nesse instante?
b) Qual será a velocidade da flecha ao abandonar a corda? A massa da flecha é de 50
g. Despreze a resistência do ar e a massa da corda.
16) (UNICAMP 2006) Um brinquedo que muito agrada às crianças são os lançadores
de objetos em uma pista. Considere que a mola da figura a seguir possui uma
constante elástica k = 8000 N/m e massa desprezível. Inicialmente, a mola está
comprimida de 2,0 cm e, ao ser liberada, empurra um carrinho de massa igual a 0,20
kg. O carrinho abandona a mola quando esta atinge o seu comprimento relaxado, e
percorre uma pista que termina em uma rampa. Considere que não há perda de
energia mecânica por atrito no movimento do carrinho.
a) Qual é a velocidade do carrinho quando ele abandona a mola?
b) Na subida da rampa, a que altura o carrinho tem velocidade de 2,0 m/s?
17) Uma bolinha de massa 3 kg e abandonada de cima de uma rampa de 0,8 m de altura.
Sabendo-se que na regiao a aceleracao da gravidade vale 10 m/s2, encontre a velocidade da
bolinha quando chega ao solo plano. Despreze os atritos.
18) Um corpo tem peso P = 20 N. Sob a acao de uma forca horizontal F, de intensidade 10 N, o
corpo e deslocado horizontalmente 5,0 metros no mesmo sentido da forca. Nesse
deslocamento, quais foram os trabalhos realizados pelas focas F e P? Considere g = 10m/s2
19) Um corpo C, representado na figura, desloca se no sentido da forca F1 de intensidade 2,0
N. Ha ainda atuando sobre o corpo a forca F2 de 1,0 N. Durante um deslocamento de modulo
2,0 m, calcule os trabalhos realizados pelas forcas F1 e F2.
20)
21) Qual é a energia cinética de uma bola de massa 0,3 kg no instante em que a sua velocidade é
4 m/s?
22) Considere uma pedra de massa 3 kg que cai de uma altura de 6 m em relação ao solo. Qual é
a sua energia cinética no instante em que atinge o solo? Determine também o valor de sua
velocidade. Dado: g= 10 m/s2.
23) Um corpo de massa 2 kg desliza sobre um plano horizontal e atinge uma mola com
velocidade de 4 m/s, comprimindo-a. A mola está no plano horizontal como nas figuras
anteriores. Desprezando os atritos, calcule a energia ganha pela mola.
24) Um corpo de massa 20 kg está localizado a 6 m de altura em relação ao solo. Dado g= 9,8
m/s2, calcule sua energia potencial gravitacional.
25) Um ponto material de 40 kg tem energia potencial gravitacional de 800 J em relação ao
solo. Dado g= 10 m/s2, calcule a que altura se encontra do solo.
26) Um corpo de massa 2 kg move-se com velocidade constante de 4 m/s. Calcule a energia
cinética do corpo.
Qual será a energia cinética quando a velocidade for duplicada?
27) Uma bola é chutada em direção ao gol e abandona o pé do jogador com velocidade de 10
m/s. Qual será a velocidade da bola quando estiver a uma altura de 1,8 m do solo? Desprezando
a resistência do ar, considere g= 10 m/s2.