Determinação do Fator de Dissipação

DETERMINAÇÃO DO FATOR DE DISSIPAÇÃO
PERDAS DIELÉTRICAS
Eng. José Arinos Teixeira Jr
1. Condutividade residual
2. Perdas por polarização
3. Perdas por descargas parciais
Gases : Os gases geralmente tem perdas extremamentes baixas. O mecanismo de perdas ou é por
condução residual ou por descargas parciais ou por ambos,
Líquidos : Para líquidos polares temos os três tipos de perdas, sendo que as perdas por polarização são
predominantes em certos casos. As perdas neste tipo de líquido são bem maiores que para líquidos não
polares. Para líquidos não polares as perdas são por condução e descargas parciais. Em líquidos
isolantes puros elas são extremamente baixas,
Sólidos : O mecanismo de perdas varia muito com o tipo de estrutura molecular. Apresenta combinações
dos três tipos de perdas.
CIRCUITOS EQUIVALENTES
Para representar as perdas dielétricas inerentes a uma estrutura isolante quando submetida a
um campo elétrico alternado, faremos uso do diagrama fasorial representado na figura 1 a seguir.
FIGURA 1 . Diagrama fasorial de um dielétrico submetido a uma tensão CA.
Todo dielétrico submetido a tensões CA de freqüência relativamente baixas, apresentam uma
corrente adiantada da tensão por um ângulo ϕ. Esta corrente pode ser decomposta em três
componentes principais:
a) Corrente de deslocamento ou capacitiva I d : Esta corrente é responsável pelo processo de carga e
descarga da capacitância geométrica C, em virtude do campo aplicado ser alternado, esta corrente
existe em forma de regime permanente. Ela é proporcional a tensão, freqüência e a capacitância.
Está sempre adiantada de 90° graus elétricos.
b) Corrente de absorção I abs : Esta corrente é composta de duas outras, a primeira é responsável pela
energia elétrica armazenada a cada meio ciclo que retorna a fonte quando da alternância do campo.
Ela é conseqüência do processo de formação de um campo elétrico pelo fenômeno da polarização. A
segunda é responsável pela energia elétrica dissipada na forma de efeito Joule, ou seja, pela fricção
no movimento dos íons ou na rotação dos dipolos elétricos. Nos dielétricos sob efeito de tensão CC,
esta última é desprezível, no entanto, nos casos de campos alternados, ela é parte primordial na
composição das perdas. A primeira corrente está 90° elétricos adiantada da tensão e a segunda está
em fase com a tensão.
c) Corrente de condução I c : É a corrente devido aos portadores de carga livres do material. Ela está
sempre em fase com a tensão aplicada e é proporcional a tensão e condutância do material.
3.1) CIRCUITO SÉRIE
i.exe
CIRCUITO EQUIVALENTE SÉRIE
tgδ =
cos ϕ =
Ur
=
U
Ur
R I
= s = ω Rs Cs
I
Uc
ω Cs
Rs ⋅ I
( Rs ⋅ I )
2
⎛ I ⎞
+⎜
⎟
⎝ ω ⋅ Cs ⎠
2
=
ω ⋅ Rs ⋅ Cs
(ω ⋅ Rs ⋅ C s ) 2 + 1
tgδ = cos ϕ = ω ⋅ R s ⋅ C s
3.2) CIRCUITO PARALELO
CIRCUITO EQUIVALENTE PARALELO
Por definição, podemos escrever que :
tgδ =
U Rp
Ir
1
=
=
I c U ⋅ω ⋅ C p ω ⋅ R p ⋅ C p
=
tgδ
(tgδ ) 2 + 1
cos ϕ =
Ir
=
I
U Rp
(U
Rp
) + (U ⋅ ω ⋅ C )
2
2
1
=
(
1+ ω ⋅ Rp ⋅ Cp
p
)
2
Analogamente ao deduzido para o circuito série, temos que a seguinte desigualdade é
verdadeira, ou seja, ω ⋅ R p ⋅ C p >> 1, e a equação do fator de potência pode ser escrita como:
tgδ = cos ϕ =
1
ω ⋅ Rp ⋅Cp
3.3) CONVERSÃO DE CIRCUITO SÉRIE PARA PARALELO E VICE-VERSA
Série para paralelo:
Cp =
Cs
1 + ( tgδ )
2
=
Cs
1 + (ω ⋅ Rs ⋅ Cs )
2
⎛
⎞
⎛
1 ⎞⎟
1
⎜1+
⎟
=
⋅
R p = Rs ⋅ ⎜⎜ 1 +
R
s
2⎟
2 ⎟
⎜
tg
δ
⋅
⋅
ω
R
C
(
)
⎠
⎝
⎝ (
s
s) ⎠
Paralelo para série:
(
Cs = C p ⋅ 1 + ( tgδ )
Rs =
1+
2
)
Rp
1
( tgδ ) 2
⎛
1
= Cp ⋅ ⎜1+
⎜
ω ⋅ Rp ⋅ C p
⎝
(
=
(
Rp
1+ ω ⋅ Rp ⋅ Cp
)
)
⎞
⎟
2 ⎟
⎠
2
4) ENSAIO DE CAPACITÂNCIA E FATOR DE DISSIPAÇÃO
Existem muitas maneiras de se medir o ângulo de perdas. Uma maneira muito popular é a
utilização de instrumentos cuja tensão de operação é de 5 ou 10 kV e medem geralmente o ângulo
ϕ = 90 0 − δ , através do cosseno deste ângulo. Para ângulo δ pequeno
tgδ ≅ cos ϕ . A este ensaio, denominamos Ensaio do Fator de Potência do
complementar a δ, ou seja
podemos escrever que
Isolamento, que é facilmente conduzido nos locais onde os equipamentos estão instalados, bastando
apenas a desenergização dos mesmos para as medições do fator de potência. É o método preferido
pelas concessionárias de energia elétrica para manutenção preventiva de seus equipamentos, onde o
estado do isolamento é acompanhado periodicamente.
4.1) ENSAIO DO FATOR DE POTÊNCIA DO ISOLAMENTO
Os ensaios de isolamento por fator de potência foram primeiramente efetuados nos Estados
Unidos, por volta de 1917, por fabricantes de cabos, para fins de pesquisa e controle de qualidade dos
materiais empregados. No campo, a utilização deu-se por volta de 1929, para verificação do isolamento
de equipamentos de subestações.
Atualmente é rotina fazer-se a medição periódica do fator de potência do isolamento dos
equipamentos elétricos, para avaliação de seu comportamento ao longo dos anos ou constatação de
avarias eminentes.
O instrumento básico para medição do fator de potência do isolamento é apresentado na figura 4
a seguir:
4.2) MEDIÇÃO DE CAPACITÂNCIA E FATOR DE DISSIPAÇÃO (tg δ)
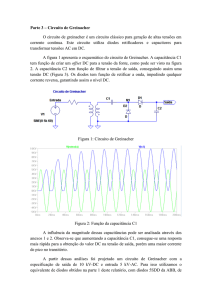
DIAGRAMA DA PONTE DE SCHERING
•
R3 , R4 , C 4 : representam as décadas de resistores e capacitores, os quais são utilizados para
equilibrar o circuito em ponte. O detector de nulo (G) e demais periféricos (reguladores de potencial
de guarda, cabos de dupla blindagem, etc) fazem parte da baixa tensão da ponte.
•
Um divisor de tensão CA, para efetuar a medição da tensão aplicada pelo transformador elevador.
•
Um transformador elevador ou outro tipo de fonte para fornecer a tensão de ensaio.
Pela variação sucessiva de R3 e C 4 , conduz-se a ponte ao estado de equilíbrio, através da
deflexão nula do galvanômetro. Nestas condições podemos escrever:
Z& 1 Z& 2
=
Z& 3 Z& 4
Admitindo para C x um circuito equivalente série e para C N uma capacitância pura (fator de
perdas muito pequeno), temos:
Z& 1 = Rx +
Z& 2 =
1
j ⋅ ω ⋅ Cx
1
j ⋅ω ⋅ CN
Z& 3 = R3
Z& 4 =
R4
1 + j ⋅ ω ⋅ R4 ⋅ C 4
Substituindo as quatro equações anteriores na equação de equilíbrio da ponte e comparando as
partes real e imaginária, obtemos:
Rx =
R3 ⋅ C 4
CN
Cx =
R4 ⋅ C N
R3
Como utilizamos o circuito equivalente série para C x , o fator de dissipação é dados por:
tgδ = ω ⋅ R4 ⋅ C4