Assunto:- Série de exercícios do tipo prova: Eletromagnetismo e

Página
1 de 2
CURSO
Eletroeletrônica -
DATA
___ / ___ / ___
COMPONENTE
ALUNO
DOCENTE
RA:
Prof. Romeu Corradi Júnior [www.corradi.junior.nom.br]
Assunto:- Série de exercícios do tipo prova: Eletromagnetismo e Eletricidade
Básica
Eletricidade Básica:
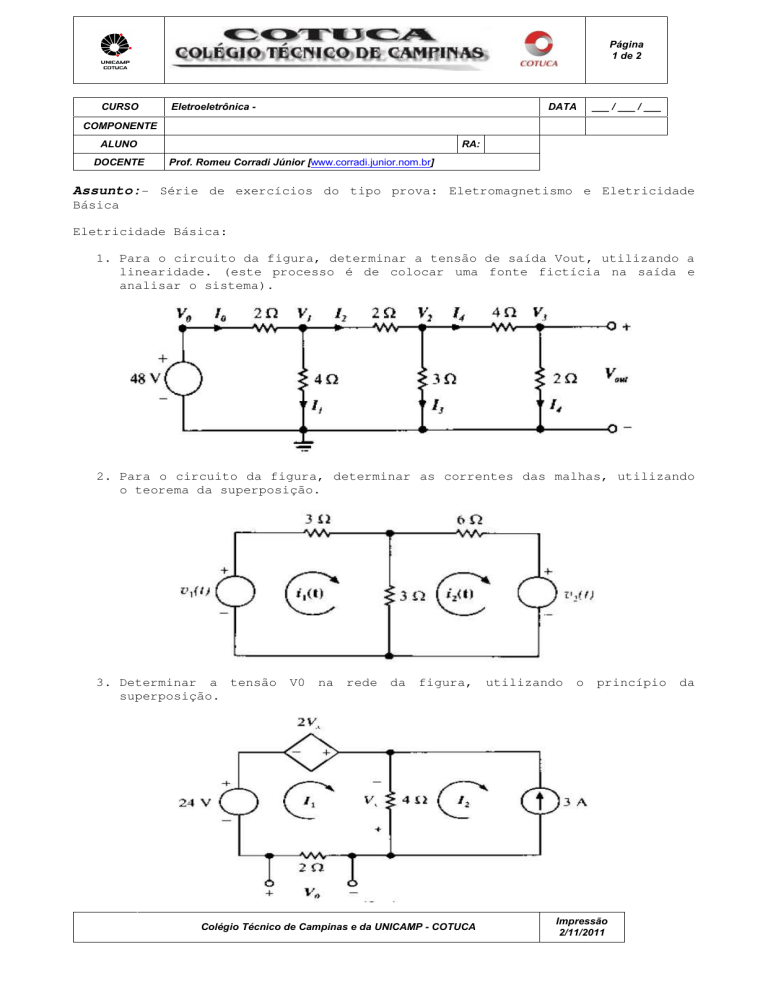
1. Para o circuito da figura, determinar a tensão de saída Vout, utilizando a
linearidade. (este processo é de colocar uma fonte fictícia na saída e
analisar o sistema).
2. Para o circuito da figura, determinar as correntes das malhas, utilizando
o teorema da superposição.
3. Determinar a tensão
superposição.
V0
na
rede
da
figura,
Colégio Técnico de Campinas e da UNICAMP - COTUCA
utilizando
o
princípio
Impressão
2/11/2011
da
4. Para o circuito da figura,
transformação de fontes.
determinar
à
corrente
I0,
utilizando
5. Para o circuito da figura abaixo, determinar a tensão V0, utilizando
transformação de fontes.
Eletromagnetismo:
1. A chave do circuito da figura que segue fecha-se em t = 0. Determine i2(t)
para t > 0.
2. As duas chaves do circuito que segue são fechadas em t = 0. Determine
i1(t), i2(t) e i3(t) para t > 0.
1
– EXERCÍCIOS – Solução_ 4ºBim_2011 Eletricidade Básica
1) Para o circuito da figura, determinar a tensão de saída Vout, utilizando a
linearidade.
Assumiremos que a tensão de saída seja Vout = 1 V e calcularemos o valor da fonte
de tensão.
V
Nessas condições V 3 = Vout = 1 V e I 4 = 3 = 0,5 A
2
V2
V2 = 4.I 4 + V3 = 3.V ⇒ I 3 =
= 1. A Usando-se a LKC, tem-se: I2 = I3 + I4 = 1,5 A
3
V
Então V1 = 2.I 2 + V 2 = 6.V ⇒ I 1 = 1 = 1,5.A Aplicado-se a LKC novamente, temos
4
I0 = I1 + I2 = 3 A e finalmente V 0 = 2.I0 + V 1 = 12 V.
Portanto, assumindo que Vout = 1 V produz ma fonte de tensão de 12 V. Entretanto,
48
a tensão real da fonte é 48 V e dessa forma a tensão real é 1V .
=4 V
12
2) Para o circuito da figura, determinar as correntes das malhas, utilizando o
teorema da superposição.
(2.a)
As correntes i 1(t) e i 2(t) tem componentes devidas a v1 (t) e v2 (t).
Fazendo com que a fonte v1(t) atue sozinha, v2(t) deve ser zero, temos o circuito da
figura (2.b)
(2.b)
2
v1 (t )
v (t )
v (t )
3 '
= 1
e i 2' (t ) =
.i1 (t ) = 1
3 x6
5
3 +6
15
3+
3+ 6
Fazendo com que a fonte v2(t) atue sozinha, v1(t) deve ser zero), temos o circuito da
figura (2.c).
i1' (t ) =
(2.c)
v (t )
3 "
i1" (t ) =
.i 2 (t ) = − 2
3+3
15
v 2 (t)
2.v ( t )
=− 2
e
3 x3
15
6+
3+ 3
A corrente total é a soma das duas parcelas.
i 2" (t ) = −
i1 (t ) = i1' (t ) + i 1" ( t ) =
v 1 (t ) v 2 (t )
−
5
15
e
i 2 (t ) = i 2' (t ) + i 2" (t ) =
v1 ( t ) 2v 2 (t )
−
15
15
3) Determinar a tensão V 0 na rede da figura, utilizando o princípio da superposição.
(3.a)
Com apenas fonte de corrente funcionando, temos o circuito da figura (3.b)
(3.b)
3
2.V’x = 4(I’ 1 – I’ 2) + 2.I’ 1
V’x = -4(I’ 1 – I’ 2)
essas equações produzem I’ 1 = −
36
72
A e V’0 =
V
14
14
I’ 2 = - 3 A
Para a fonte de tensão operando, temos o circuito da figura (3.c)
As equações são:
(3.c)
e
24 + 2 V”x = 6.I”1
V”x = - 4.I”1
24
48
Dessas equações obtemos I” 1 =
A e desse modo V”0 = −
V
14
14
72 48 24
Portanto V 0 = V’0 + V”0 =
−
=
V
14 14 14
4) Para o circuito da figura, determinar a corrente I0, utilizando transformação de
fontes.
(4.a)
Transformando as fontes reais de tensão: (60 V; 6 Ω) e (15 V; 3 Ω) em fontes de
corrente, respeitas as polaridades, obtemos o circuito da figura (4.b)
(4.b)
4
Somando algebricamente as fontes ideais de corrente (10 – 5 = 5 A) e combinando
6x 3
os resistores
= 2Ω , obtemos o circuito da figura (4.c)
6+3
(4.c)
Aplicando a divisão de corrente, obtemos I0 =
2
.5 = 2 A
2+ 3
5) Para o circuito da figura abaixo, determinar a tensão V0, utilizando transformação
de fontes.
(5.a)
Transformando a fonte de tensão (64 V, 4 Ω) em fonte de corrente (16 A, 4 Ω) e
combinando os resistores de 4 Ω e 12 Ω, obtemos o circuito da figura (5.b).
(5.b)
Transformando a fonte de corrente (16 A, 3 Ω) em fonte de tensão (48 V, 3 Ω),
associando com a fonte de tensão independente obtemos (36 V, 3 Ω), que
transformando em fonte de corrente e associando os resistores de 3 Ω e 6 Ω temos
o circuito da figura (5.c)
(5.c)
5
Transformando a fonte de corrente (12 A, 2 Ω) em fonte de tensão (24 V, 2 Ω) e
associando as duas resistências de 2 Ω em série; que transformando novamente em
fonte de corrente (6 A, 4 Ω ) e associando as duas fontes de corrente (6 A, 4 Ω) e
(2 A, 0), obtemos o circuito da figura (5.d)
(5.d)
Aplicando divisão de corrente e a lei de Ohm, achamos V 0
4
V0 =
x8 x1 = 4 V
4 + 3 +1