Estabilidade e Compensação

2
Capítulo
N O TA S D E A U L A , R E V 6 . 0 – U E R J 2 0 1 6 . 2 – F L Á V I O A L E N C A R D O R Ê G O B A R R O S
Eletrônica 4
Estabilidade e Compensação
 Flávio Alencar do Rego Barros
Universidade do Estado do Rio de Janeiro
E-mail: [email protected]
Notas de aula – versão 6.0
O capítulo 2 (Estabilidade e Compensação) trata de modo mais detalhado as
formas de analisar a estabilidade dos circuitos realimentados e as técnicas, métodos e
procedimentos, chamados compensação, para garantir tal estabilidade. Na versão
2015.2, nas aulas, serão suprimidas algumas partes que constam deste material, como
Critério de Nyquist, Análise no Plano-s para Estabilidade, Método de Compensação por
Equalizador. No entanto, os textos e as figuras relativas a estes assuntos foram mantidos
neste material de apoio. Estão incluídos textos e figuras sobre: análise de estabilidade,
Bode assintótico, critério de Nyquist, Routh-Hurwitz, Yen, compensação.
Estas notas de aulas se destinam a reduzir o trabalho de cópia do aluno durante
as aulas (indica-se manter em cada aula, cada aluno a sua cópia), mas também oferecer
material de apoio na forma de exercícios propostos e referências onde o aluno poderá
complementar seu estudo. É importante perceber que este material NÃO esgota o que o
aluno deve ler durante o curso, nem mesmo substitui a participação em sala de aula,
devendo ser encarado apenas como material de apoio. Alertamos que também pode
acontecer nestas notas de aula alguns erros de digitação ou de outra natureza, a ideia é
corrigi-los ao longo das aulas, à medida que forem descobertos.
Notas de aula – versão 6.0
Índice do capítulo 2:
12. Análise de Estabilidade.............................................................................................49
Margem de Ganho (MG) e Margem de Fase (MF)...............................................50
13. Análise de Estabilidade – Bode Assintótico
52
14. Critério de Nyquist
54
15. Método de Análise –Routh-Hurwitz..........................................................................56
16. Limites de Yen...........................................................................................................57
17. Compensação.............................................................................................................60
Compensação por Polo Dominante.......................................................................60
Compensação por Cancelamento Polo-Zero.........................................................63
Compensação por Equalizador..............................................................................64
Anexo C – 2ª. LISTA.........................................................................................................i
Notas de aula – versão 6.0
UERJ 2016
Pag. 49
Eletrônica 4
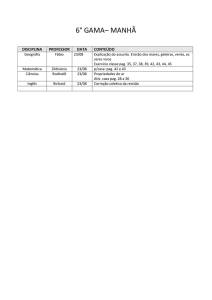
12. Análise de Estabilidade
O efeito da realimentação na estabilidade de circuitos depende dos polos da função
A(s). Numa análise de A(s) no plano imaginário, caso os polos se localizem no SPD
(semiplano da direita), o circuito é instável. Sem demonstração, apenas por ilustração,
se A(s) tem polo simples (vide Figura 51 a seguir) não haverá instabilidade para
qualquer valor de aoβ (ou aor, segundo a notação do cap. 1):
Baixas frequências:
a( s) =
ao ( s )
⇒ A( s ) =
(s + w1 )
ao s

[1 + ao β ] s +

a( s) =
Altas frequências:
w1 

1 + ao β 
ao w2
ao w2
⇒ A( s ) =
(s + w2 )
s + w2 + ao w2 β
Estabilidade e Pólo Simples
Im
a0β = 0
-w2
Re
-w1
a0β = ∞
Estabilidade e Pólo Duplo
Im
a0β = ∞
a0β = 0
a0β = ∞
-w4
-w3
-w2
-w1
Re
a0β = ∞
Figura 51: Estabilidade e Polos
Ainda acompanhando na Figura 51 acima, se A(s) tem polo duplo, e da mesma
forma não existem polos no SPD:
Notas de aula – versão 6.0
UERJ 2016
Pag. 50
Eletrônica 4
a( s) =
Baixas frequências:
ao s 2
ao s 2
⇒ A( s ) =
(s + w1 )(s + w2 )
(s + w1 )(s + w2 ) + ao βs 2
Altas frequências:
a( s) =
ao w3 w4
ao w3 w4
⇒ A( s ) =
(s + w3 )(s + w4 )
s 2 + (w3 + w4 )s + w3 w4 + ao w3 w4 β
A estabilidade, porém, pode não acontecer para três polos ou mais, além do que
a análise é muito mais complicada. O que vamos fazer neste capítulo é verificar a
estabilidade de circuitos realimentados, porém, olhando de um ponto de vista prático.
De início, analisaremos três métodos: Margens (de Ganho e Fase), Bode, Nyquist e
Hurwitz (os dois primeiros, gráficos, os dois últimos, analíticos).
Margem de Ganho (MG) e Margem de Fase (MF)
a(s)
Como A f = 1 + a( s )r ( s ) , o circuito será instável se:
ganho de malha aberta
a ( s ) r ( s ) = −1 ⇒ A f ( s ) → ∞
o
circuito estável requer a ( s )r ( s ) < 1 quando ∠a ( s )r ( s ) = 180 ,
então
a
estabilidade
do
amplificador
pode
ser
analisada
pelos
plots
de
a ( s ) r ( s ) e ∠a ( s ) r ( s ) .
Define-se Margem de Ganho (MG) e Margem de Fase (MF):
MG = − a ( s ) r ( s ) dB
180 o
diferença entre 0 dB e o módulo na frequência que a fase
chega a 180°.
MF = ∠a ( s ) r ( s )
diferença entre a fase na frequência que o módulo alcança
0 dB e a fase de -180°.
Notas de aula – versão 6.0
UERJ 2016
Pag. 51
Eletrônica 4
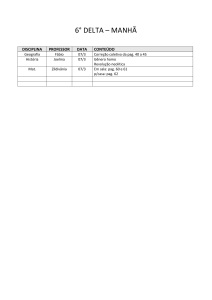
Na Figura 52 a seguir se encontram as visualizações gráficas destas duas
definições. Para o circuito ser estável é rigorosamente necessário que:
MG > 0
MF > 0
Em termos práticos, MG representa o quanto |ar| pode ser aumentado antes do
amplificador se tornar INSTÁVEL. É praxe de projeto garantir MG > 10 dB e também
MF > 50° .
Margem de Ganho – Margem de Fase
20
10
|ar|dB 1
a
2
0
b
MG
-10
-20
1
10
4
100
1000
w (rad/seg)
1000
w (rad/seg)
0º
-60º
c
ar
-120º
MF
d
2
-180º
1
10
100
3
Figura 52: Margens de Ganho e de Fase
Observe agora que se w1 é a frequência onde o ganho de malha aberta é unitário:
a ( jw1 ) β = 1⋅ ∈ jθ ⋅ ⋅ ⋅ ⋅ ⋅θ = 180 o − MF
então, o ganho de malha fechada é:
 1  jθ
  ∈
β
a ( jw1 )
= 
A f ( jw1 ) =
1 + a ( jw1 ) β
1+ ∈ jθ
1
⇒ A f ( jw1 ) =
β
1 + jθ
1
=
β
(1 + cos θ )2 + sen 2 θ
Notas de aula – versão 6.0
UERJ 2016
Pag. 52
Eletrônica 4
se fizermos MF = 50° ⇒ θ = 180°- 50 = 130°
1
β
⇒ A f ( jw1 ) =
=
1.18
β
2
1 + cos130 o  + sen 2 130 o


significa um pico de 1.4 dB (20 log 1.18) acima do ganho de meia-banda (20 log 1/β)
MF diminui ⇒ pico aumenta (MF = 10° ⇒ pico= 15.1 dB)
Se:
MF aumenta ⇒ pico diminui (MF = 90° ⇒ pico= -3 dB !!!)
Perceba, portanto, a solução de compromisso envolvida!
Observe os picos acima de meia banda para diversas situações:
Pico acima da meiabanda (dB)
15.2
9.2
5.7
3.3
1.5
MF
10°
20°
30°
40°
50°
0
-3
60°
90°
θ
170°
160°
150°
140
MF limítrofe
prático 130°
120°
90°
O problema deste método de análise de estabilidade é que nos obriga a soluções
gráfica e computacionalmente intensivas.
13. Análise de Estabilidade – Bode Assintótico
Trata-se de um método gráfico (podem também ser tiradas conclusões analíticas),
simples, que fornece o grau de estabilidade do circuito (estável, fracamente estável ou
instável).
Condição de estabilidade:
a ( s ) r ( s ) = −1
Frequentemente r(s) é puramente resistivo: r (s ) = β
Notas de aula – versão 6.0
UERJ 2016
|A|dB
⇒ 20 log a( s ) β
Pag. 53
Eletrônica 4
|a|dB
=
|1/β|dB
−
20 log a( s )
1
20 log
β
ganho de malha
aberta
ganho do
ganho de
canal direto
realimentação
(FABRICANTE)
(SEU CIRCUITO)
Visualização gráfica desta equação:
Bode Assintótico
Módulo
(dB)
condição de instabilidade:
ganho de
malha aberta
20 log | a ( s ) β |= 20 log | a ( s ) | −20 log |
(1/β)dB
180º ?
ganho de
Realimentação
(SEU CIRCUITO)
ganho de
canal direto
(FABRICANTE)
1
β
|
|a|dB
w (escala log)
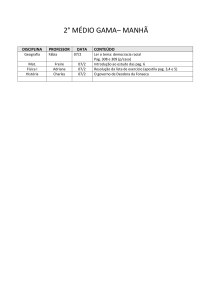
Figura 53: Bode Assintótico
Aquele ponto indicado na Figura 53 corresponde ao risco de instabilidade, se o
gráfico de fase para este valor de w passar por 180°.
Numa abordagem prática, cada polo de a(s) – canal direto - acarreta uma
“quebra” de –20 dB/dec na curva de módulo e uma “queda” de -90° na curva de fase.
Assim, se a interceptação entre |a|dB e |1/β|dB se dá com uma diferença de angulação de
menos que –40 dB/dec o circuito é considerado ESTÁVEL; se igual a –40 dB/dec o é
FRACAMENTE ESTÁVEL (no ponto crítico a fase se aproxima assintoticamente de 180°); se mais que –40 dB/dec o circuito é INSTÁVEL.
Notas de aula – versão 6.0
UERJ 2016
Pag. 54
Eletrônica 4
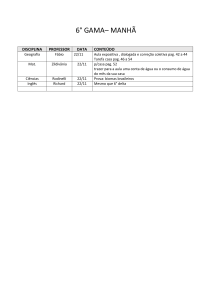
Na Figura 54 a seguir são mostrados diversos gráficos de redes de realimentação
para uma única plotagem de ganho de canal direto. Conforme o ponto de interceptação,
os respectivos circuitos terão o seu status quanto à estabilidade.
AV ,dB
Lista 2-6
1 / β2
1 / β1
1 / β4
w
ganho
sem
compensação
1 / β3
Figura 54: Exemplos - Bode Assintótico
Vejamos a seguir métodos analíticos.
14. Critério de Nyquist
“Um amplificador realimentado é estável se ele não apresenta polos
positivos ou contendo zero na sua parte real”.
O diagrama de Nyquist corresponde ao mapeamento do plano-s no planoa(jw)β:
Notas de aula – versão 6.0
UERJ 2016
Pag. 55
Eletrônica 4
Critério de Nyquist
Im
Im
SPE
SPD
plano-a(s)β
plano-s
Re
Re
Im[a(jw)β]
Im[a(jw)β]
plano-a(s)β
plano-a(s)β
-1
Re [a(jw)β]
-1
Re [a(jw)β]
instável
estável
Figura 55: Critério de Nyquist
O número de vezes que o contorno circunda o ponto crítico (-1 + j0) –
corresponde ao ponto crítico - é igual ao número de raízes com parte real positiva.
A relação entre MG, MF e Critério de Nyquist é ilustrada na Figura 56 a seguir:
Margens de Ganho e Fase/Critério de Nyquist
Im[a(jw)β]
MG = 20 log |
-α
-1
Re [a(jw)β]
φM
MF = φ M
Figura 56: Relações Nyquist e Margens de Ganho e Fase
Notas de aula – versão 6.0
1
α
|
UERJ 2016
Eletrônica 4
Como MG = 20 log
1
α
Pag. 56
, se tiver múltiplas intercessões no semi-eixo negativo,
MG é da intercessão que mais se aproxima do ponto crítico. Quanto à Margem de Fase:
MF = φ M , ou seja, ângulo entre eixo real negativo e ponto de interceptação com o
círculo unitário.
15. Método de Análise – Routh-Hurwitz
Considere R( s ) = 1 + a( s) β = an s n + an −1s n −1 + an − 2 s n − 2 ⋅ ⋅ ⋅ + a0 raízes de Af(s). O
método Routh-Hurwitz consiste em construir uma matriz como ilustrado na Figura 57 a
seguir e utilizar o seguinte critério quanto à estabilidade:
“Todos sinais da 1ª coluna (an, an-1, b1, c1, ...) são iguais”. Isto significa (a ausência de
inversões de sinal) que não existem raízes no SPD. Para casos não degenerativos, o
número de mudanças no sinal da 1ª coluna da matriz é igual ao número de raízes no
SPD do polinômio R(s).
Método de Routh-Hurwitz
R ( s ) = 1 + a ( s ) β = an s n + an−1s n−1 + ... + a0
sn
an
an-2
an-4
........
sn-1
an-1
an-3
an-5
........
sn-2
b1
b2
b3
........
sn-3
c1
c2
c3
........
b1 =
an−1an−2 − an an−3
an−1
b2 =
an−1an−4 − an an−5
an−1
.
.
.
.. . . . . . . . . . . . . . . . . . . . . .
s0
sinais
iguais
c1 =
b1an−3 − b2 an−1
b1
c2 =
b1an−5 − b3an−1
b1
.
.
.
Figura 57: Método Routh-Hurwitz
Notas de aula – versão 6.0
UERJ 2016
Pag. 57
Eletrônica 4
EXEMPLO: Dado R(s), verifique se o amplificador realimentado é estável ou instável.
a)
R ( s ) = s 4 + 10 s 3 + 35s 2 + 50 s + 24
b)
R ( s ) = s 3 + 2 s 2 + 2 s + 40
c)
R( s) = s 4 + s 3 + 2s 2 + 2s + 3
d)
R( s) = s 3 + s 2 + 4s + 4
SOLUÇÃO: Em sala de aula. Respostas: estável; instável; instável; estável, mas pode
oscilar.
16. Limites de Yen
Trata-se do limite de realimentação que pode ser aplicada a um amplificador sem tornálo instável (utiliza o critério de Routh-Hurwitz para descobrir a máxima realimentação
aoβo).
ao s 3
Sejam b1, b2,...,bn os pólos nas baixas freqüências: a ( s ) =
(s + b1 )(s + b2 )(s + b3 )
ao a1a 2 a3
a1, a2,...,an os pólos nas altas freqüências: a ( s) = (s + a )(s + a )(s + a )
1
2
3
1) 3 POLOS (de baixa, portanto, 3 zeros na origem)
R( s) = (1 + ao β )s 3 + (b1 + b2 + b3 )s 2 + (b1b2 + b1b3 + b3b2 )s + b1b2b3
(formato 3 polos de baixa)
sejam: A = 1 + ao β
C31 = b1 + b2 + b3 = B
C32 = b1b2 + b1b3 + b2b3 = C
C33 = b1b2b3 = D
...
C nm = soma das combinações dos n polos
tomados m a m (em produtos).
Notas de aula – versão 6.0
UERJ 2016
Pag. 58
Eletrônica 4
Routh-Hurwitz:
s3
s2
s1
A
C
B
BC − AD
B
D
D
0
s0
como A, B e D > 0 ⇒
BC − AD
>0
A
(para ser estável)
(b1 + b2 + b3 )(b1b2 + b1b3 + b2b3 ) − (1 + ao β )b1b2b3
b1 + b2 + b3
⇒ b1b2 + b1b3 + b2b3 −
>0
(1 + ao β )b1b2b3
>0⇒
b1 + b2 + b3
b
b
b
b
b
b2
1 + ao β < 1 +
+1+ 1 +1+ 3 +1+ 2 + 3 ⇒
b3 b3
b2
b2
b1 b1
b +b
b +b
b +b
ao β < 1 2 + 1 3 + 2 3 + 2
b3
b2
b1
Analisando dois casos limites:
i)
b1 = 100
polo dominante (o pior entre os melhores casos)
b2 = 10
b3 = 10 ⇒ ao β < 11 + 11 + 0.2 + 2 ⇒ Y3b = 24.2
ii)
b1 = b2 = b3
polos iguais (pior caso)
ao β < 2 + 2 + 2 + 2 ⇒ Y3b = 8
Se fizermos a mesma análise para 4 e 5 polos, vamos obter:
Notas de aula – versão 6.0
UERJ 2016
Pag. 59
Eletrônica 4
Limites de Yen
No. de
pólos
Limites de Yen (baixas)
Pólos
Pólo
coincidentes
dominante
Condições
3
BC – AD = 0 -> Y3b = a0 β|MAX
B = C31 C = C32 D = C33 A = 1 + a0β
8
24.2
4
BCD – AD2 – B2E = 0 -> Y4b = a0 β|MAX
B = C4 1 C = C4 2 D = C4 3 E = C4 4
4
11.1
5
(BC – AD)(BE – AF)D – (BE – AF)2B – (BC – AD)2
2.4
7.3
Figura 58: Limites de Yen
EXEMPLO: O formato de R(s) para altas frequências (3 polos) é:
R( s) = (1 + ao β )s 3 + (b1 + b2 + b3 )s 2 + (b1b2 + b1b3 + b3b2 )s + b1b2b3
Prove que o limite de Yen para altas frequências é igual ao seu limite para baixas
( Y3a = Y3b ).
SOLUÇÃO: Possivelmente em sala de aula.
Notas de aula – versão 6.0
UERJ 2016
Eletrônica 4
Pag. 60
17. Compensação
Se um amplificador realimentado se torna instável, existem dois métodos básicos para
estabilizá-lo. O primeiro, reduzir o ganho de malha aberta (ar), mas pode ter
consequências inaceitáveis. O segundo, compensação, significa acrescentar uma rede
que garanta MF ≥ 50° e MG ≥ 10 dB:
SEM COMPENSAÇÃO
COM COMPENSAÇÃO
Figura 59: Rede de Compensação
São três os principais métodos de compensação que analisaremos:
polo dominante (Lag)
cancelamento polo-zero (Lag-Lead)
equalizador (Lead)
Em todos métodos a ideia é recuar o ponto em que a curva de decibéis corta a
origem (|a|dB = 0) em uma freqüência que seja GARANTIDO que ∠a não chegou
ainda em 180°, portanto, longe da instabilidade.
Compensação por Polo Dominante
No método POLO DOMINANTE, a ideia é inserir um polo (fd) de modo que
|a´|dB passe em 0 dB no primeiro polo f1 de |a|dB não compensado. Como ilustraremos
numa próxima figura o preço da estabilidade é a redução da banda!
Uma estrutura RC colocada na saída do amplificador direto oferece as condições de
polo dominante, senão vejamos:
Notas de aula – versão 6.0
UERJ 2016
Pag. 61
Eletrônica 4
1
sC p
V
1
Hp = o =
=
1
V1
1 + sR p C p
Rp +
sC p
Figura 60: Estrutura RC para Compensação Polo Dominante
chamando
wp =
V
1
1
⇒ o =
=Hp
s
R pC p
V1
1+
wp
Agregando esta estrutura RC à saída do canal direto, como ilustrado na Figura
61 abaixo:
Compensação Pólo Dominante
a´
|a|dB
BW antes
Vi
V1
a
Rp
V0
-20dB/dec
R0
wp
w1
w (escala log)
ANTES DA COMPENSAÇÃO
|a´|dB
wp =
BW depois
-20dB/dec
wp
wp =
w1
w (escala log)
DEPOIS DA COMPENSAÇÃO
Figura 61: Compensação por Polo Dominante
Notas de aula – versão 6.0
w1
a
1
R pC p
Cp
UERJ 2016
Pag. 62
Eletrônica 4
Os resultados mostrados na Figura 61 são oriundos de:
Figura 62: Estrutura de Compensação por Polo Dominante
ra´ = aH p =
ra
1+ j
w
wp
⇒ ra´
dB
= 20 log ra − 20 log
aplicando a condição de polo dominante:
w
0 = 20 log ra − 20 log 1
wp
w
⇒ w p = 1 → na região em que |ra|dB tem –20 dB/dec
ra
EXEMPLO: Dimensione a rede de compensação por polo dominante para o seguinte
amplificador realimentado. Sabe-se que o AMP OP apresenta:
Ri = 1MΩ; Ro = 75Ω e RM =
− 10 4




s
s
s
1 +
1 +
1 +





6
6
6
 2π ⋅ 10  2π ⋅ 10 ⋅ 10  2π ⋅ 30 ⋅ 10 
Figura 63: Exercício da Lista 2-11
SOLUÇÃO: Em sala de aula. Respostas: 1.57 KHz; 1.35 µF
Compensação por Cancelamento Polo-Zero
A ideia é inserir um zero antes de um polo, para cancelar o 1° polo e garantir 0 dB no
segundo polo da função original. É, pois, por construção, menos redutor de banda que o
Notas de aula – versão 6.0
w
wp
UERJ 2016
Pag. 63
Eletrônica 4
método anterior. A rede de compensação responsável por isto é ilustrada na Figura 64 a
seguir.
Compensação Cancelamento Pólo-Zero
V1
|a|dB
Ra
V0
BW antes
Rb
-20dB/dec
Cc
wp
wpz
w1
w2
w (escala log)
ANTES DA COMPENSAÇÃO
w pz =
w2
a
w pz =
1
( Ra + Rb + R0 )Cc
wz = w1
|a´|dB
BW depois
-20dB/dec
wz = w1 =
wpz
w1
w2
w (escala log)
1
RbCc
DEPOIS DA COMPENSAÇÃO
Figura 64: Compensação por Cancelamento Polo-Zero
Para este circuito:
Rb +
1
sCc
1 + sRb Cc
V
H pz = o =
=
1
1 + (Ra + Rb )sCc
V1
Ra + Rb +
sCc
(numerador tem um
zero, denominador tem um polo). Se:

w
a1 + j
wz
1
1
wz =
∴ H pz = 
e wp =
w
(Ra + Rb )Cc
Rb C c
1+ j
wp
w
wz
então: H pz =
w
1+ j
wp
1+ j

w
a1 + j
wz
⇒ a´ = aH pz = 
w
1+ j
wp
Notas de aula – versão 6.0






UERJ 2016
Eletrônica 4
Pag. 64
Aplicando a condição de cancelamento polo-zero:
f
0 = 20 log a − 20 log 2
fp
w z = w1
⇒
f
fp = 2
a
f z = f1
então:
wp =
1
(Ra + Rb + Ro )Cc
w z = w1 =
e
1
Rb C c
Compensação por Equalizador
É similar ao cancelamento polo-zero, exceto que o polo ocorre “depois” do zero:
H eq =
s + w z eq
s + w peq
w p eq >> w z eq
Nestes termos, a condição de compensação para o equalizador é:
 w
0 = 20 log a − 20 log 1
w
 peq

w1
 ⇒ w
=
p
eq

a

Agora, o segundo polo de a(s) é cancelado pelo zero da rede de compensação. A rede de
compensação e os resultados são ilustrados na Figura 65 a seguir.
Notas de aula – versão 6.0
UERJ 2016
Eletrônica 4
Pag. 65
Compensação Equalizador
Cc
V0
V1
w peq =
w1
a
wzeq = w2
Ra
Rb
wzeq =
1
Ra Cc
w peq =
1
( Ra || Rb )Cc
Figura 65: Compensação por Equalizador
Conclusão: Esta é a solução mais economizadora de banda, porém, isto ocorre à custa
da diminuição do ganho. Por isto, vamos dar menor importância a ela.
EXEMPLO: Para o circuito abaixo, AV é o ganho do amplificador em malha aberta,
polos do AM POP em 1 MHz, 4 MHz e 40 MHz; AV0 = 72dB .
a) Demonstre que:
c / compensação
}
´
=
AV
1 + jwRc Cc
1 + jwC c  Rc + R1 + r // R´ 


s / compensação
⋅
AV
{
b) Determine BW (banda passante).
c) Calcule Rc e Cc considerando R1 = R// R´, R = 1K e R´ >> R.
SOLUÇÃO: Possivelmente em sala de aula. Respostas: ≅1 KHz; 81 nF e 2Ω.
Notas de aula – versão 6.0
UERJ 2016
Eletrônica 4
Pag. 66
Anexo C - 2a. LISTA
(Assunto: Análise de Estabilidade)
2.1) (Critério de Estabilidade) Se a0 = 100 e a(s) é dado abaixo, calcule a0βMAX de
modo a atender ao critério de Bode Assintótico de estabilidade.
a0 s 3
a( s) =
( s + 100)( s + 200)( s + 500)
2.2) (Critério de Estabilidade) Idem, calcule AfMIN se:
a( s) =
100 s 3
( s + 100) 2 ( s + 1000)
2.3) (Critério de Estabilidade) Idem:
a( s) =
100s 4
( s + 100)( s + 200)( s + 500)( s + 1000)
2.4) (Margens de ganho e de fase) Sabe-se que é praxe manter uma margem de fase
mínima de 50°, o que nos dá um pico de 1.14 dB acima do ganho de meia banda.
a) Determine que MF nos daria 0 dB acima do ganho de meia banda;
b) Determine que MF nos daria 15.2 dB acima do ganho de meia banda
2.5) (Estabilidade, Bode assintótico) Considere o amplificador com o ganho de canal
direto dado abaixo. Utiliza-se a rede de realimentação dada. Determine se o circuito
é ou não estável pelo método de Bode assintótico.
a ( jf ) =
1000
(1 + jf )(1 + j
f
)
10
Notas de aula – versão 6.0
UERJ 2016
Pag. 67
Eletrônica 4
2.6) (Estabilidade, Bode assintótico) Quais das redes de realimentação aplicadas ao
amplificador de canal direto cujo diagrama de Bode assintótico é dado na figura
abaixo serão instáveis ou fracamente estáveis. Explique.
A V ,d B
L ista 2-6
1 / β2
1 / β1
1 / β4
w
1 / β3
gan h o
sem
com p en sação
2.7) (Método de Routh-Hurwitz) Se R(s) = 1 + a(s) β = s4 + 10s3 + 35s2 + 50s + 24,
analise as condições de estabilidade pelo método de Routh-Hurwitz.
2.8) (Método de Routh-Hurwitz) Idem para R(s) = s4 + s3 + 2s2 + 2s + 3.
2.9) (Método de Routh-Hurwitz) Idem para R(s) = s3 + s2 + 4s + 4.
2.10) (Método de Routh-Hurwitz) Idem para R(s) = s3 + 2s2 + 2s + 40.
2.11) (Compensação) Dimensione a rede de compensação por polo dominante para o
circuito abaixo, sabendo-se:
Ri = 1 MΩ
RM =
(1 +
Ro = 75 Ω
s
2π .106
)(1 +
10 − 4
s
2π .(10 x10 6 )
)(1 +
s
2π .(10 x10 6 )
(circuito na próxima página)
Notas de aula – versão 6.0
)
UERJ 2016
Eletrônica 4
Pag. 68
Lista 2-11
R2
R1
Vi
180 Ω
51 Ω
Vo
Ri
Ro
2.12) (Compensação) Para o circuito abaixo, AV é o ganho do amplificador em malha
aberta. Se os polos do AMP OP estão em 1 MHz, 4 MHZ e 40 MHZ, e se AVo = 72
dB:
a) Demonstre que:
A = AV
Vf
1 + jwRc Cc
1 + jwCc ( Rc + R1 + R // R , )
b) Determine a banda passante do amplificador compensado.
c) Calcule RC e CC considerando R1 = R//R´ e R = 1K e R´ >> R
Lista 2-12
Vs
o
R
Rc
R‘
V
o
Cc
R1
2.13) (Estabilidade) Se AVo = 1000 e f1 = 20 Hz é o único polo do amplificador usado
abaixo:
a) Trace em um mesmo gráfico as curvas assintóticas de Bode do amplificador
canal direto e da realimentação (1/β);
Notas de aula – versão 6.0
UERJ 2016
Eletrônica 4
Pag. 69
b) Determine se o circuito realimentado é estável, instável ou fracamente estável.
Lista 2-13
Vs
+
Vo
C
0.1 microF
R1
600 K
R2
300 K
2.14) (Compensação)
a) A função de transferência de um AMP OP apresenta polo em f1 = 1 MHz e
ganho em baixas frequências de 44 dB. Usa-se compensação de polo dominante.
Responda em que frequência fica o ganho compensado de 0 dB e calcule fd.
b) Idem, se o ganho em baixas frequências é de 68 dB.
2.15) (Limites de Yen) Se o formato de três pólos em baixas frequências apresenta:
R(s) = 1 + a(s) β = (1 + a0β)s3 + (b1 + b2 + b3)s2 + (b1b2 + b1b3 + b2b3)s + b1b2b3
a) Prove que o limite de Yen é 24,2 se os polos são do tipo dominante (p, p, 10p)
b) Repita a prova para polos coincidentes (p, p, p) dando limite de Yen igual a 8.
c) Qual é o pior caso? Por quê?
2.16) (Limites de Yen) Se o formato de três polos em altas frequências é dado por:
R(s) = s3 + (a1 + a2 + a3)s2 + (a1a2 + a1a3 + a2a3)s + a1a2a3(1 + a0β), prove que Y3a =
Y3b (este último foi calculado no exercício anterior).
Notas de aula – versão 6.0