Cap I (Algarismos significativos, gráficos, vetores, revisão)

F-107
Capítulo I
Mauro M.G. de Carvalho
CAPÍTULO I
MEDIDAS E ALGARISMOS SIGNIFICATIVOS
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
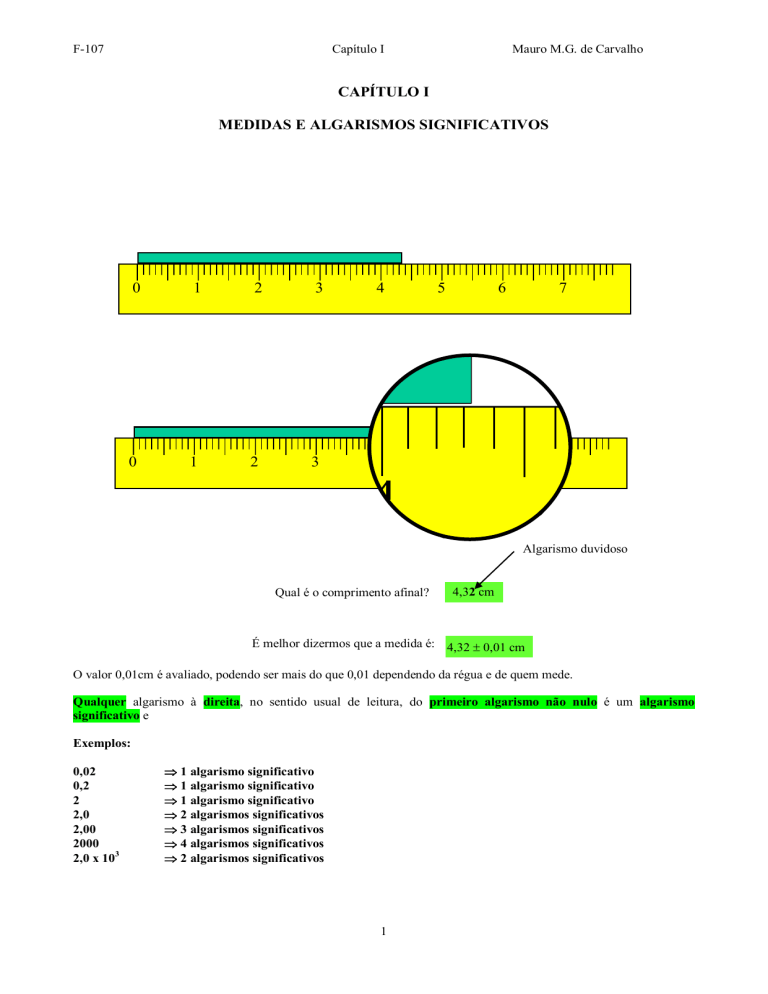
Algarismo duvidoso
Qual é o comprimento afinal?
4,32 cm
É melhor dizermos que a medida é: 4,32  0,01 cm
O valor 0,01cm é avaliado, podendo ser mais do que 0,01 dependendo da régua e de quem mede.
Qualquer algarismo à direita, no sentido usual de leitura, do primeiro algarismo não nulo é um algarismo
significativo e
Exemplos:
0,02
0,2
2
2,0
2,00
2000
2,0 x 103
 1 algarismo significativo
 1 algarismo significativo
 1 algarismo significativo
 2 algarismos significativos
 3 algarismos significativos
 4 algarismos significativos
 2 algarismos significativos
1
F-107
Capítulo I
Mauro M.G. de Carvalho
Regras de arredondamentos
N = 3,87XY
N = 3,88
Se X > 5
N = 3,87
Se X < 5
N = 3,88
se Y ≥ 5
N = 3,87
se Y < 5
Se X =5 
Operações levando em conta os algarismos significativos
Soma:
135 + 2,73 - 10,57 - 4,3 + 0,8  123
Multiplicação e divisão:
24,63 x 12,3 = 302 no de algs.significativos = ao que tem menos
Valor Médio e Desvio Padrão:
Sejam X1, X2, X3... as diversas medidas de uma mesma grandeza.
O Valor Médio da grandeza é: X = <X> = (X1 + X2 + X3 + ... + XN) / N
O Desvio Padrão da medida é dado por , onde: <>2 = (<X> - X1)2  (<X> - X2)2 + ........+ (<X> - XN)2 / (N-1)
Exemplo:
20,34
20,32
20,38
MEDIDAS (em metros)
20,30
20,35
20,37
20,35
20,35
<X> = (20,34 + 20,32 + 20,38 + 20,30 + 20,35 + 20,37 + 20,35 + 20,35) / 8
<X> = 20,34 m
= [ (20,34-20,34)2 + (20,34-20,32)2  (20,34-20,38)2  (20,34-20,30)2 + (20,34-20,35)2  (20,34-20,37)2  ...
+(20,34-20,35)2  (20,34-20,35)2 ] / 7
 = 0,03
A medida se expressa por : 20,34  0,03
2
F-107
Capítulo I
Mauro M.G. de Carvalho
REVISÃO DE MATEMÁTICA
Relações trigonométricas
senB =AC/BC
cosecB = 1/senB
cosB = AB/BC secB = 1/cosB
tgB = AC/AB
tgB= senB/cosB
(AB)2 +(AC)2 = (BC)2
sen2B+cos2B = 1
tg2B+1 = sec2B
B
A
C
Fig.1 – Triângulo equilátero
sen(x±y) = senx.cosy ± cosx.seny
cos(x±y) = cosx.cosy  senx.senyy
sen2x = 2senx.cosx
cos2x = cos2x – sen2x
Gráficos
Y
(1,4)
(-4,2)
Representação de pontos (x,y) no gráfico cartesiano.
Na figura estão os pontos (1,4); (-4,2); (-3,-3); (2, -5)
X
Exercício: (a) Marque os pontos (1,1), (3,2), (-2,3),
(-4, -1), (-2,3)
(b) Marque os pontos (-4,-1), (-2,0), (0,1), (2,2) e
(4,3).
Em seguida ligue esses pontos. Qual a realção que eles
guardam entre si?
(-3,-3)
(2,-5)
Fig.2 – Eixos Cartesianos
3
F-107
Capítulo I
Mauro M.G. de Carvalho
Cosideremos a equação: y = x2 + x - 2
Calculando y para alguns valores de x (abaixo) podemos
traçar a curva ao lado
x
-3
-2
-1
0
1
2
3
y
4
0
-2
-2
0
4
10
F
Fig. 3 – Parábola
4
F-107
Capítulo I
Mauro M.G. de Carvalho
Derivada
Fixando x1 e fazendo x2 x1 (fig.4a), a secante se transforma em tangente à curva em (x1,y1) (fig.4b) e:
y
dy

x
dx
(a)
y2
y1
x2
x1

(b)
y1
x1

tgα 
dy
dx
Fig4: A secante (em vermelho) de transforma em tangente quano x 2 → x1
5
F-107
Capítulo I
Mauro M.G. de Carvalho
dy/dx é a derivada da curva em (x1,y1).
Portanto, a derivada num ponto dá a tangente trigonométrica (tgdo ângulo que a tangente geométrica, no ponto
considerado, forma com o eixo dos X.
6
F-107
Capítulo I
Mauro M.G. de Carvalho
VETORES
sentido
Módulo
A
direção
Nomenclatura: A é normalmente representado por A (em negrito). O módulo de A é representado por A (sem negrito)
Se A e B têm o mesmo módulo direção e sentido, então A = B
Algumas propriedades importantes:
B
A
a) Soma de vetores: Método geométrico
A
A+B
A+B
B
b) Propriedade comutativa
A
A
B
A
C
B
C
C
A + B+ C = B + C + A = C + B + A
c) Propriedade associativa
(A+B) + C = A+ (B+ C)
d) Produto de escalar por vetor
A
k3 A
k2A
K1>1
0<K2<1
K3<0
7
k1A
B
F-107
Capítulo I
Mauro M.G. de Carvalho
Diferença entre vetores: Note que se B + (A - B) = A . Essa operação pode ser visualizada abaixo
A
A-B
B
B
A
Soma (diferença) de vetores colineares. É só somar (subtrair) seus módulos:
A+B
Soma de vetores através de suas projeções
Projeção de um vetor nos eixos
cartesianos
y
y
C
A
Ay
A


x

B

Ax
eixo x = Rx
eixo y = Ry
2
2Ry 2
Rtg
+R
x
 y= R
Rx
x
Ax =Acos
Ay=Asen
A2 = Ax2+Ay2
Ry
tg 

Rx
Ay
A
R
x
8
F-107
Capítulo I
Mauro M.G. de Carvalho
Produto escalar entre dois vetores A e B:
A.B = ABcosonde  é o aângulo entre A e B.
Produto vetorial entre dois vetores A e B:
AxB = ABsenonde  é o ângulo entre A e B.
O resultado do produto vetorial entre A e B é um vetor perpendicular a A e a B e cujo sentido pode ser dado pela regra
da mão direita. O produto vetorial não é comutativo: A x B = -BXA
AxB
B
A
O produto escalar é uma escalar e dá projeção de A sobre B multiplicada por B (em módulo). O produto vetorial é um
vetor cujo módulo é a área do paralelogramo formado a aprtir de A e B.
A.B = ABcos 




AxB = ABsen
A
A


B
B
Acos
Asen
Área do paralelogramo: base x altura = B.AsenAxB
9
F-107
Capítulo I
Mauro M.G. de Carvalho
EXERCÍCIOS
1) Na figura abaixo, dê o resultado das medidas de AB.
A
B
0
1
2
A
biol
AB =
B
AB =
0
1
2
biol
0
1
2
biol
AB =
0
1
2
biol
AB =
2) Quantos algarismos significativos têm os números abaixo:
a) 98,75
b) 2,00
c) 0,003 d) 0,0450
e) 3000
f) 1,0 x 103
3) Faça as aproximações solicitadas:
a)  = 3,14159
Para uma, duas, três e quatro casas decimais
b) e = 2,71828
Para uma, duas, três e quatro casas decimais.
c).me = 9,1091 x 10-31kg
Para uma e duas casas decimais
d) e = 1,6021 C
Para uma e duas casas decimais
4) Transforme:
a) 2,3 mm
b) 2,303 m
c) 2,8 km
d) 2,0kg →g
e) 2,753mg
→m
→ mm
→m
→g
5) Resolva as contas abaixo:
a) 2,0 cm x 3 =
b) 2,0 cm x 3,0 cm =
c) 2,215 cm x 2,20 mm =
d) 0,73g / 1,00 cm3 =
e) 1,000m + 20,5cm =
f) 1200 -23,2 + 1,9 -0,8+0,2+10 =
g) sen 13o =
10
F-107
Capítulo I
Mauro M.G. de Carvalho
6) Calcule x nas figuras abaixo:
5,0 cm
2,0 cm
30o
x
x
(a)
(b)
6,0 cm
x
30o
75o
75o
x
(d)
4,0 cm
(c)
5o
2,0 cm
x
60o
x
10,0 m
(e)
(f)
7) Considere o gráfico abaixo:
a) Onde a função é crescente?
b) Onde é decrescente?
c) Onde a derivada é positiva?
d) Onde a derivada é negativa?
e) Onde a derivada é nula?
f) Onde estão os máximos da curva?
g) Onde estão os mínimos da curva?
h) Onde a derivada é crescente?
i) Onde a derivada é decrescente?
j) Qual o valor máximo da função no intervalo
considerado?
k) Onde a função é nula?
l) Qual a grandeza física que a derivada representa?
litros
5
10
20
30
horas
-5
11
F-107
Capítulo I
A
C
Mauro M.G. de Carvalho
D
E
B
Cada quadrado desta página tem lado equivalente a 1N. (a) Qual o módulo das forças A, B, C, D e E acima.? (b)
Abaixo, calcule geométricamente: A+B; A+B+D; A-D; D+E-A; A+C-D
(c) Calcule o módulo das forças resultantes nas operações realizadas no item (b); Determine a força F talque
F+A+B+C+D+E=0
12
F-107
Capítulo I
Mauro M.G. de Carvalho
REVISÃO DE FÍSICA BÁSICA
Cinemática
x= xo + vt
x = xo + vot + (1/2)at2
v2 = vo2 + 2a x
 = /t
v = R
Movimento relilíneo uniforme
Movimento relilíneo com aceleração constante
Movimento relilíneo com aceleração constante
Velocidade angular (movimento circular uniforme)
Movimento circular uniforme
Ondas
v = f
Onda progressiva de comprimento de onda frequência f e velocidade v.
T = 1/f
Relação entre período T e frequência f
No caso da luz v = c = 3x 108 m/s
Propriedades exclusivas das ondas:
a) Difração
b) Polarização
Eletromagnetismo
F= qE
W qE.d
V = W/q = E.d
Energia
K = (1/2)mv2
U = - G (m.MT)/r
U = mgh
Força F sobre uma carga q num ponto onde o campo elétrico é E (equação vetorial)
Trabalho da força F ao se deslocar de d na sua direção sentido.
Diferença de potencial elétrico entre dois pontos distantes de d na direção e sentido do campo
elétrico constante E
Energia cinética
Energia potencial gravitacional d massa m a uma distância r do centro da terra (mssa MT)
Diferença de energia potencial gravitacional entre dois pontos quando diferença de altura
entre eles é h e a distância à superfície terrestre é muito menor do que o raio da terra.
Sistemas de Unidades:Definem as unidades fundamentais de massa (M), comprimento (L) e tempo (T). Para
eletricidade é definida a unidade de carga.
Os principais são: Sistema Internacional de Unidades (SI) que é o MKS (M de metro, K de kilograma e S de segundo).
Muito usado em laboratório é o CGS ( Centímetro, Grama e Segundo).
Nos dois sistema a unidade de carga é o Coulomb.
Temperatura não faz parte de nenhum sistema, mas em ciências o Kelvin é o mais usado.
Todas as unidades da mecânica são derivadas das três unidades que definem o sistema.
Exemplos:
Sistema
Definiçãos
Força (F = m.a)
Momento Linear
Trabalho ( = F.d)
Potência (P = W/t)
Pressão (P = F/A)
Densidade (d= m/V)
Torque(N = F.d)
Momento Angular
MKS
Unidades básicas Nome (símbolo)
kg.m/s2
Newton (N)
kg.m/s
kg.m2/s2
Joule (J)
2 3
kg.m /s
Watt(W)
kg/(m.s2)
Pascal (P)
kg/m3
N.m
kg.m2/s
CGS
Unidades básicas Nome (símbolo)
g.cm/s2
dina (dyn)
g.cm/s
g.cm2/s2
erg
2 3
g.cm /s
erg/s
g/(cm.s2)
dyn/cm2
3
g/cm
dyn.cm
g.cm2/s
Unidades em eletricidade:Não vamos utilizar o CGS eletrostático. Somente o SI. A Unidade de carga é o Coulomb (C).
Sistema
Definição
Força (F = m.a)
Trabalho ( = F.d)
Potência (P = W/t)
DDP ( /q)
Campo Elétrico (F/q)
Corrente (q/t)
Unidades básicas
kg.m/s2
kg.m2/s2
kg.m2/s3
kg.m2/(C.s2)
kg.m/(C.s2)
C/s
13
MKS
Nome (símbolo)
Newton (N)
Joule (J) e Watt.hora (W.h)
Watt(W)
J/C = Volt (V)
N/C = V/m
Ampère (A)
F-107
Capítulo I
Mauro M.G. de Carvalho
Na física atômica usa-se uma unidade de energia chamada eletronvolt (eV). Isto ocorre porque o Joule é uma unidade
muito grande para medir as energias envolvidas. Define-se 1 eV como sendo a energia cinética de um elétron livre
acelerado por uma ddp de 1 V. Observe que  = q.1V. Logo:
1eV = 1,6 x 10-19C.1V = 1,6 x 10-19 J
Aplic.1: Qual a velocidade do elétron com energia de 1 eV?
A energia cinética para o elétron é dada por T = (1/2)mv2
Existe um sistema chamado MK*S. Neste sistema as unidades básicas são o metro, o quilograma-força (kgf) e o
segundo. Quilograma-força é unidade de força definida como: 1 kgf é o peso de um corpo de 1kg de massa onde a
aceleração da gravidade é 9,8 m/s2. Logo, 1kgf = 1kgx9,8m/s2 = 9,8 N
Este sistema de unidades é usado com uma certa frequência em engenharia mecânica.
Algumas unidades não pertencem a sistema algum, mas são usadas até hoje em certos nichos por uma questão de
tradição.Exemplos:
Os médicos usam centímetro de mercúrio para medir pressão arterial;
O frentista do posto de gasolina usa o psi (Pound force per Square Inch) para calibrar pneus;
Alguns encanadores usam a polegada para dar o diâmetro dos tubos;
Os fabricantes de alimentos usam a caloria para o valor da energia gerada pelos alimentos;
Alguns livros antigos usam o Angstron (Ǻ) para a medida de comprimento de onda da luz. 1Ǻ = 10 -10m.
Espectro da radiação eletromagnética
A luz visível é uma pequena parte do espectro da radiação eletromagnética. A figura abaixo mostra o espectro em
função do comprimento de onda da radiação (http://www.infoescola.com/wp-content/uploads/2007/12/espectro-visivelda-luz.jpg)
Observe que a luz visível tem comprimento de onda compreendido entre aproximadamente 380nm (violeta) e 740 nm
(vermelho)
14