Astrofísica Extragaláctica! Aula #5"

Astrofísica Extragaláctica!
Aula #5"
Karín Menéndez-Delmestre"
Observatório do Valongo!
Diferenças!nas!propriedades!usicas!gerais!entre:!
Galáxias!de!6po!tardio!
–  Razão!bojo/disco!baixa!
!
–  Cor:!azul!
–  Formação!estelar!a6va!
–  Bastante!gás,!poeira!
–  População!estelar:!!
!mistura!de!nova!+!!velha!
–  regiões!HII:!!
•  maior!quan6dade,!maior!
tamanho!e!maior!
luminosidade!nas!de!6po!
tardio!comparado!aquelas!em!
galáxias!de!6po!anterior!
!
Galáxias!de!6po!anterior!
–  Razão!bojo/disco!maior!!
!!!bojo!proeminente!
–  Passivas!(SFR!baixo)!
–  Cor:!vermelho!
–  Pouco!gás,!poeira!
–  População!estelar:!!
!mistura!de!nova!+!!velha!
Tópicos!(Parte!I)!
1.  Revisão:!Formação!e!Evolução!Estelar!
2.  Introdução!a!Extragalác6ca!
3.  Propriedades!Gerais!das!Galáxias!
3.1.!Morfologia!das!galáxias!
! !3.1.1.!Sistemas!de!Classificação!
! !3.1.2.!Propriedades!Astrousicas!dos!Tipos!de!Galáxias!
– Correlações!usicas!(na!escala!absoluta)!
– Propriedades!em!função!do!ambiente!
3.2.!Populações!Estelares!
3.3.!Função!de!Luminosidade!
4.  Propriedades!Gerais!das!Galáxias!Elíp6cas!
5.  Propriedades!Gerais!das!Galáxias!Espirais!
!
Distribuição!de!6pos!morfológicos!!
•  Oemler+74:!estudo!de!15!aglomerados!ricos!em!galáxias!!
–  Classificação!de!aglomerados!segundo:!!
① Porcentagem!de!galáxias!S/S0/E!
② Presença!de!uma!galáxia!cD!
③ Segregação!espacial!de!6pos!de!galáxias!
Oemler!
Distribuição!de!6pos!morfológicos!–!!!
Efeito!`Butcher`Oemler !
!
O!qué!mostra!este!
gráfico?!
campo
“fração'azul”!=!
fração!de!galáxias!
luminosas!azuis!!
associada!com!
aglomerados!
densos!!!
Butcher!&!Oemler!(1978)!Ap!J!219,!18!
Em 1978, Butcher & Oemler observaram dois aglomerados distantes (3C 2
a z = 0.39) e encontraram um excesso de galáxias azuis em relação à popul
próximos. Em 1984, estes mesmos autores estudam mais 33 aglomerados ent
firmam o excesso de galáxias azuis (este excesso é medido em relação à sequên
Este efeito ficou conhecido como efeito Butcher–Oemler.
A figura 124 ilustranova!determinação!do!efeito,!
o efeito Butcher–Oemler assim como um trabalho mais
baseado!em!fotometria!CCD!de!44!
Carvalho (2000) com uma
nova determinação deste efeito, baseado em fotomet
do catálogo de Abell. aglomerados!do!catálogo!de!Abell.!
Distribuição!de!6pos!morfológicos!–!!!
Efeito!`Butcher`Oemler’!
!
•  Resultado!de!um!estudo!
de!>30!aglomerados!em!!!!!!!!! 0.4
0.003!<!z!<!0.54:!
0.3
`  excesso!de!galáxias!
0.2
azuis!em!relação!à!
0.1
população!Épica!de!
0
aglomerados!no!
universo!próximo!
-0.1
fB no campo
fB
Figur
Butcher & Oemler (1984)
Ajuste de Butcher & Oemler (1984)
Margoniner & de Carvalho (2000)
Ajuste de Margoniner & de Carvalho (2000)
0
0.05
0.1
0.15
0.2
z
0.25
0.3
0.35
azuis
traço
lho o
ler (1
traba
ner &
espess
fração
0.4
•  A!fração!azul!associada!com!aglomerados!densos!aumenta!
É importante levarmos em conta onde no aglomerado a fração de galáxia
significa6vamente!com!redshiÖ!
125 mostra esta dependência para 5 aglomerados. Notamos que a fração de g
a distância ao centro do aglomerado.
!!Há!uma!evolução!das!galáxias!em!aglomerados!num!passado!
rela6vamente!próximo!!
0.4
!
0.3
0.1
0
ler (198
trabalh
ner & d
espesso
fração d
Butcher & Oemler (1984)
Ajuste de Butcher & Oemler (1984)
Margoniner & de Carvalho (2000)
Ajuste de Margoniner & de Carvalho (2000)
Distribuição!de!6pos!morfológicos!–!!!
-0.1
A!fração!azul
0
!
0.05
0.1
0.15
0.2
z
0.25
0.3
0.35
0.4
É importante levarmos em conta onde no aglomerado a fração de galáxias
•  É!importante!considerar!onde!no!aglomerado!a!fração!de!galáxias!
125 mostra esta dependência para 5 aglomerados. Notamos que a fração de ga
azuis!!é!medida.!!
a distância ao centro do aglomerado.
<fB>
•  Dependência!da!fração!
de!galáxias!azuis!com!a!
distância!ao!centro!do!
<fB>
aglomerado!
!
•  a!fração!de!galáxias!azuis!
aumenta!com!a!distância!
ao!centro!do!
aglomerado.!
0.4
0.3
Figu
fraç
dist
rado
lho,
0.2
0.1
5 aglomerados com
0.16 < z < 0.18
0
0
0.2
0.4
0.6
0.8
R (Mpc)
1
1.2
1.4
1.6
Distância do centro (Mpc)
O efeito B-O mostra que há uma evolução das galáxias em aglomerados em u
Margoniner!&!de!Carvalho,!2000!
próximo, ao contrário do que se constata dos próprios aglomerados, que aprese
suas propriedades (por exemplo, temperatura e metalicidade do gás intra-aglom
5.11.5
Perda de gás por pressão de arraste
Frac6on!of!popula6on!
Distribuição!de!6pos!morfológicos!–!!!
!
O!qué!mostra!este!
gráfico?!
A!fração!de!
espirais!diminui!
a!medida!que!a!
densidade!local!
aumenta;!a!
fração!de!S0s!e!
Es!aumenta.!
log!(densidade!projetada!no!céu,!Mpc`2)!!
Dressler+80
Distribuição!de!6pos!morfológicos!–!!!
Relação!raio`morfologia`densidade!
Dressler
`  a!fração!de!galáxias!de!um!dado!6po!
morfológico!está!fortemente!
correlacionada!com!a!densidade!
superficial!local!(Mpc`2)!em!que!as!
galáxias!se!encontram!
!
! Esta!relação!pode!ser!lida!como...!
“o!número!de!espirais!diminui!em!
direção!ao!centro!dos!
aglomerados,!enquanto!o!das!
elíp6cas!aumenta”!
Dressler+80
•  Dressler!estudou!55!aglomerados!ricos!e!
15!regiões!de!“campo”!(>6000!galáxias):!
Distribuição!de!6pos!morfológicos!–!!!
Relação!raio`morfologia`densidade!
•  Considerando!aglomerados!
irregulares!(menos!ricos!e!
estruturados),!Dressler!
determinou!que!a!correlação!
com!raio!não!é!tão!forte!!
!!o!efeito!fundamental!é!a!
densidade!local!
Dressler
Distribuição!de!6pos!morfológicos!–!!!
Função!de!Luminosidade!(FL)!
Função de luminosidade de galáxias separadas por tipo
em função do ambiente
•  As!diferenças!
em!LFs!de!
ambientes!
diferentes!são!
principalmente!
devido!às!
proporções!
diferentes!de!
6pos!de!galáxia!
(S/Irr/S0/E)!
http://msowww.anu.edu.au/~jerjen/dial_a_LF/dial_a_lf.html
Segregação!morfológica!de!galáxias!em!
aglomerados!
•  Juntando!o!trabalho!de!Oemler+74!e!a!relação!morfologia`
densidade!(Dressler+97):!
!As!propriedades!das!galáxias!dependem!tanto!da!estrutura!do!
aglomerado!como!da!posição!da!galáxia!no!aglomerado!(devido!à!
dependência!na!densidade).!!
!
•  Aglomerados!ricos!e!regulares:!
–  !possuem!uma!fração!de!elíp6cas!e!len6culares!elevada!!
–  a!fração!de!Es!e!S0s!aumenta!em!direção!ao!centro!
!
•  Aglomerados!pobres!e/ou!irregulares!:!
–  apresentam!uma!fração!elevada!de!espirais!!
–  pouco/nenhum!gradiente!radial!de!população!
Nature!vs.!Nurture!–!o!dilema!
•  “Nature”!
–  Galáxias!de!dis6ntos!6pos!nascem!em!ambientes!diferentes:!
elas!são!intrínsicamente!diferentes!desde!o!começo!(i.e.,!por#
natureza)!
•  Galáxias!de!6po!anterior!nascem!em!aglomerados!
•  “Nurture”!
–  Ambientes!densos!transformam!espirais!e!irregulares!em!
galáxias!E/S0!via!interações!e!remoção!de!gás.!
•  perda!do!gás!pelo!efeito!de!pressão!de!arraste!(ram3
pressure,#em!inglês).!
! Resulta!na!diminuição!da!a6vidade!de!formação!
estelar!nestas!galáxias!
!
!
Distribuição!de!6pos!morfológicos!–!!!
Evolução!da!Relação!Morfologia`Densidade!
•  Considerando!a!abundância!de!S0s!em!aglomerados!próximos…!!!!!!!!!!!!
transformação!S!!S0!em!aglomerados!densos!
z~0!
Dressler!et!al!(1997)!Ap!J!490,!577!
z~0.5!
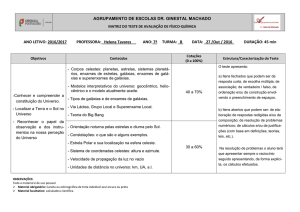
Gás!em!galáxias!de!aglomerados!
HI!(gás!atómico)!no!aglomerado!Coma!
5.11 Efeitos do Aglomerado nas galáxias e vice-versa
116
Deformações da emissão do HI
29°00'
160-098
8764
160-076
5390
Declinação (B1950)
K 1258+287
8884
160-058
7614
160-055
7041
160-257
5821
28°30'
IC 4040
7867
160-095
5479
28°00'
160-106
6876
160-260
7974
160-086
7481
K1255+275
7398
27°30'
13h00m
Nurture?!
•  perda!do!gás!pelo!efeito!de!
Figura 126: Efeito
da pressão de arpressão!de!arraste!
raste em Coma. Os contornos espessos representam a emissão em raiostransforma!galáxias!S/Irr!em!
X, os contornos finos representam a
emissão do Hi, superpostas às imaE/S0!
gens ópticas (nı́veis
de cinza) das
galáxias (ampliadas por um fator 7).
Cada objeto tem sua identificação e
velocidade !de recessão (em km/s). A
cruz central corresponde à elı́ptica gigante NGC 4874. Figura tirada de
! diminuição!de!SFR!
Bravo-Alfaro
et al. (2000).
!
12h58m
12h56m
Ascensão reta (B1950)
da pressão de arraste. EsteBravo`Alfaro!et!al.!(2000).!
efeito também pode ser observado em emissões rádio com morfologia head-tail
em galáxias ativas em aglomerados (veja Fig. 101).
A pressão de arraste pode ser um mecanismo importante para o enriquecimento em metais do meio
intra-aglomerado, como foi discutido inicialmente por Gunn & Gott (1972). Estes autores compararam a
pressão de arraste dada por:
Gás!em!galáxias!de!aglomerados!
HI!(gás!atómico)!no!aglomerado!Coma!
5.11 Efeitos do Aglomerado nas galáxias e vice-versa
116
Deformações da emissão do HI
29°00'
160-098
8764
160-076
5390
Declinação (B1950)
K 1258+287
8884
160-058
7614
160-055
7041
160-257
5821
28°30'
IC 4040
7867
160-095
5479
28°00'
160-106
6876
160-260
7974
160-086
7481
Figura 126: Efeito da pressão de arraste em Coma. Os contornos espessos representam a emissão em raiosX, os contornos finos representam a
emissão do Hi, superpostas às imagens ópticas (nı́veis de cinza) das
galáxias (ampliadas por um fator 7).
Cada objeto tem sua identificação e
velocidade de recessão (em km/s). A
cruz central corresponde à elı́ptica gigante NGC 4874. Figura tirada de
Bravo-Alfaro et al. (2000).
K1255+275
7398
27°30'
13h00m
12h58m
12h56m
Ascensão reta (B1950)
da pressão de arraste. EsteBravo`Alfaro!et!al.!(2000).!
efeito também pode ser observado em emissões rádio com morfologia head-tail
em galáxias ativas em aglomerados (veja Fig. 101).
A pressão de arraste pode ser um mecanismo importante para o enriquecimento em metais do meio
intra-aglomerado, como foi discutido inicialmente por Gunn & Gott (1972). Estes autores compararam a
pressão de arraste dada por:
Atlas!de!Hα!em!Virgo!
Tópicos!(Parte!I)!
1.  Revisão:!Formação!e!Evolução!Estelar!
2.  Introdução!a!Extragalác6ca!
3.  Propriedades!Gerais!das!Galáxias!
3.1.!Morfologia!das!galáxias!
! !3.1.1.!Sistemas!de!Classificação!
! !3.1.2.!Propriedades!Astrousicas!dos!Tipos!de!Galáxias!
– Correlações!usicas:!!
– Propriedades!em!função!do!ambiente!
3.2.!Populações!Estelares!
3.3.!Função!de!Luminosidade!
4.  Propriedades!Gerais!das!Galáxias!Elíp6cas!
5.  Propriedades!Gerais!das!Galáxias!Espirais!
!
Tópicos!(Parte!I)!
1.  Revisão:!Formação!e!Evolução!Estelar!
2.  Introdução!a!Extragalác6ca!
3.  Propriedades!Gerais!das!Galáxias!
3.2.!Populações!Estelares!
•  Espectros!estelares!!
•  síntese!de!populações!estelares!
•  Distribuição!Bi`modal!de!cor!
3.3.!Função!de!Luminosidade!
4.  Propriedades!Gerais!das!Galáxias!Elíp6cas!
5.  Propriedades!Gerais!das!Galáxias!Espirais!
!
Espectros!integrados!de!galáxias!
•  O!espectro!integrado!de!uma!
galáxia!resulta!da!soma!das!
emissões!individuais!das!
estrelas!e!da!absorcão!do!
meio!inter`estelar.!
!
Pickles (1998).
Sunday, January 23, 2011
Espectros!integrados!de!galáxias!
14.3 Classificação espectral
214
M5V
1
0.5
0
2
K5V
1.5
1
0.5
0
2
G5V
1.5
1
fluxo (h) / fluxo (5556 Å)
•  O!espectro!integrado!de!uma!
galáxia!resulta!da!soma!das!
emissões!individuais!das!
estrelas!e!da!absorcão!do!
meio!inter`estelar.!
!
•  Se!conhecemos!a!distribuição!
de!estrelas!em!função!do!
6po!espectral!em!uma!
galáxia,!podemos!deduzir!seu!
espectro!integrado!!!Isto!!é!
chamado!síntese!de!
população!estelar!
2
1.5
0.5
0
2
F5V
1.5
1
0.5
0
2
A5V
1.5
1
0.5
0
2
A0V
1.5
1
0.5
0
2
B8V
1.5
1
0.5
0
2
05V
1.5
1
0.5
0
3500
4000
4500
5000
5500
h (Å)
7000
Pickles6500(1998).
6000
Figura 231: Espectro de estrelas da sequência principal do catálogo de Pickles (1998).
População!estelar!
•  Definição!de!uma!população!estelar!simples!
–  grupo!de!estrelas!com!uma!idade!e!composição!específica!!!!!!!!!!
(e.g.,!aglomerados!estelares)!
•  Uma!galáxia!está!composta!de!várias!populações!estelares!!!!!!!!!!
! !! !uma!“síntese!de!populações!simples”!!
! !(SSP!em!inglês:!simple#synthesis#popula?on)!
–  não!temos!acesso!as!cores!das!estrelas!individuais! !!
! Criamos!modelos!SSP!para!estudar!sistemas!complexos!!!!!!!!!!!!!!!!!
(e.g.,!regiões!estelares,!galáxias)!
–  O!ajuste!entre!a!soma!dos!espectros!que!compõe!o!modelo!e!o!
espectro!observado!nos!permite!estabelecer,!a!princípio,!a!
composição!e!o!histórico!de!formação!estelar!da!galáxia.!
!!SFH#=#star#forma?on#history!
Ingredientes!de!modelos!SSP!
•  Ingredientes!básicos!para!a!construção!de!modelos!SSP:!
–  Biblioteca!estelar!
14.3 Classificação espectral
214
2
M5V
1.5
1
0.5
(com!suas!advantagens!e!
desavantagens!respec6vas)!
–  Exemplo:!
!Pickles!stellar!library!
K5V
1.5
1
0.5
0
2
G5V
1.5
1
fluxo (h) / fluxo (5556 Å)
•  coleção!de!espectros!
individuais!das!estrelas!numa!
população!estelar!simples!
(metalicidade,!idade)!!
– Espectros!teóricos!(Teff,!
g,!Z)!ou!empíricos!!!!!!!!!
0
2
0.5
0
2
F5V
1.5
1
0.5
0
2
A5V
1.5
1
0.5
0
2
A0V
1.5
1
0.5
0
2
B8V
1.5
1
0.5
0
2
05V
1.5
1
0.5
0
3500
4000
4500
5000
5500
6000
6500
7000
h (Å)
Figura 231: Espectro de estrelas da sequência principal do catálogo de Pickles (1998).
sistema também se baseia na comparação do espectro integrado das galáxias no intervalo λ3850–λ4100,
com o espectro de estrelas (tabela 19).
Ingredientes!de!modelos!SSP!
•  Ingredientes!básicos!para!a!construção!de!modelos!SSP:!
–  Biblioteca!estelar!
–  Isocrônas!!
•  Curva#de#“mesma”#idade#
•  Curvas!isocrônas!=!curva!
que!enlaça!a!coleção!de!
posições!no!diagrama!HR!
de!um!grupo!de!estrelas!
(mesma!idade!e!
composição)!!
•  Cada!população!simples!é!
representada!por!uma!
isocrôna!
consider the logarithmic mass function:
ξ(M) = ln(10)Mφ(M).
Ingredientes!de!modelos!SSP!
Likewise, one can define the logarithmic slopes of the IMF:
b(M) ≡ −
dlogφ
dlogM
dlogξ
=b−1
dlogM
•  Ingredientes!básicos!para!a!construção!de!modelos!SSP:!
Measuring
the IMF:
–  Biblioteca!estelar!
1. Measure the apparent magnitudes of all stars down to some luminosity limit in
some (relatively local) volume.
–  Isocrônas!!
Tendência!geral:!
2. Convert to absolute magnitudes and derive a luminosity function for the stars.
Note that distance errors and dust extinction can make this step uncertain.
–  Função!inicial!de!Massa!(IMF)!
φ(M)'~'M2α''
β(M) ≡ −
3. Use the relation between stellar mass and stellar lifetime to convert the luminosity function to a mass function.
•  observações!dos!
4. Correct the mass function for any processes that may have changed the true
aglomerados!
mass function. These include (but are likely not restricted to): stellar deaths,
depending on the age of the population; ongoing star formation; dynamical
estelares!galác6cos!!
processes (e.g., some stars getting ejected from clusters); unresolved binaries.
The intrinsic function φ is then:
t
indicam!que!φ(M)!é!
φ = φ(M)
for τ < t
τ
φ = φ(M) for τ > t
dada!por:!
0
0
MS
MS
0
MS
Salpeter (1955): #(M) ~ M-2.35
!α!
=!2.35!
Scalo (1986): #(M)
~ M-2.45 M > 10 M⦿
M-3.27 1 M⦿ < M < 10 M⦿
!
anãs!marrões!!
(<0.08!Msolar)!
φ(M) = o número de estrelas de massa M
M-1.83
0.2 Mhá
⦿ < M < 1 M⦿
que nascem
quando
formação estelar:
dNestrelas = φ(M) dM;
Chabrier (2003): $(M) ~ M-1.35 M > 1 M⦿ (Salpeter)
exp{-[log (M/0.2 M⦿)]2/0.6} M < 1 M⦿
Sunday, January 30, 2011
Simpson+08:!arXiv:0807.4382!
consider the logarithmic mass function:
ξ(M) = ln(10)Mφ(M).
Ingredientes!de!modelos!SSP!
Likewise, one can define the logarithmic slopes of the IMF:
b(M) ≡ −
dlogφ
dlogM
dlogξ
=b−1
dlogM
•  Ingredientes!básicos!para!a!construção!de!modelos!SSP:!
Measuring
the IMF:
–  Biblioteca!estelar!
1. Measure the apparent magnitudes of all stars down to some luminosity limit in
some (relatively local) volume.
–  Isocrônas!!
Tendência!geral:!
2. Convert to absolute magnitudes and derive a luminosity function for the stars.
Note that distance errors and dust extinction can make this step uncertain.
–  Função!inicial!de!Massa!(IMF)!
φ(M)'~'M2α''
β(M) ≡ −
3. Use the relation between stellar mass and stellar lifetime to convert the luminosity function to a mass function.
•  observações!dos!
4. Correct the mass function for any processes that may have changed the true
aglomerados!
mass function. These include (but are likely not restricted to): stellar deaths,
depending on the age of the population; ongoing star formation; dynamical
estelares!galác6cos!!
processes (e.g., some stars getting ejected from clusters); unresolved binaries.
The intrinsic function φ is then:
t
indicam!que!φ(M)!é!
φ = φ(M)
for τ < t
τ
φ = φ(M) for τ > t
dada!por:!
0
0
0
0
M
MS
S
0
0
MS
MS
MS
MS
Salpeter (1955): #(M) ~ M-2.35
!α!
=!2.35!
Scalo (1986): #(M)
~ M-2.45
M-3.27
M-1.83
!
M > 10 M⦿
1 M⦿ < M < 10 M⦿
0.2 M⦿ < M < 1 M⦿
Chabrier (2003): $(M) ~ M-1.35 M > 1 M⦿ (Salpeter)
exp{-[log (M/0.2 M⦿)]2/0.6} M < 1 M⦿
Sunday, January
Sunday,
January 30,
30, 2011
2011
van Dokkum & Conroy 2010
consider the logarithmic mass function:
ξ(M) = ln(10)Mφ(M).
Ingredientes!de!modelos!SSP!
Likewise, one can define the logarithmic slopes of the IMF:
b(M) ≡ −
dlogφ
dlogM
dlogξ
=b−1
dlogM
•  Ingredientes!básicos!para!a!construção!de!modelos!SSP:!
Measuring
the IMF:
–  Biblioteca!estelar!
1. Measure the apparent magnitudes of all stars down to some luminosity limit in
some (relatively local) volume.
–  Isocrônas!!
2. Convert to absolute magnitudes and derive a luminosity function for the stars.
Note that distance errors and dust extinction can make this step uncertain.
–  Função!inicial!de!Massa!(IMF)!
β(M) ≡ −
3. Use the relation between stellar mass and stellar lifetime to convert the luminosity function to a mass function.
•  observações!dos!
4. Correct the mass function for any processes that may have changed the true
aglomerados!
mass function. These include (but are likely not restricted to): stellar deaths,
depending on the age of the population; ongoing star formation; dynamical
estelares!galác6cos!!
processes (e.g., some stars getting ejected from clusters); unresolved binaries.
The intrinsic function φ is then:
t
indicam!que!φ(M)!é!
φ = φ(M)
for τ < t
τ
φ = φ(M) for τ > t
dada!por:!
0
0
0
0
M
MS
S
0
0
MS
MS
MS
MS
Salpeter (1955): #(M) ~ M-2.35
!
Scalo (1986):! #(M) ~ M-2.45
M-3.27
M-1.83
!
M > 10 M⦿
1 M⦿ < M < 10 M⦿
0.2 M⦿ < M < 1 M⦿
Chabrier (2003): $(M) ~ M-1.35 M > 1 M⦿ (Salpeter)
exp{-[log (M/0.2 M⦿)]2/0.6} M < 1 M⦿
hjp://www.astro.livjm.ac.uk/~ikb/research/imf`use`in`cosmology.html!
Sunday, January
Sunday,
January 30,
30, 2011
2011
Modelos!SSP!
•  Construção!de!um!modelo!SSP:!Soma!dos!espectros!estelares!
correspondendo!aos!pontos!de!uma!isócrona!com!peso!variável,!
Espectros!individuales!
segundo!ditado!pela!IMF.!
isocróna!
IMF!
Salpeter!IMF!
Modelos!SSP:!empíricos!vs.!evolu6vos!
•  2!6pos!de!modelos:!
•  Modelos#empíricos#=!usam!espectros!reais!de!estrelas!individuais!
–  “Starlight”!(Fernandes+05)!
!
•  Modelos#evolu?vos#=!partem!de!condições!iniciais!e!usam!
modelos!para!descrever!a!evolução!da!população!estelar!
• Taxa de formação estelar (SFR, star formation ratio), Ψ
convertida em estrelas em função do tempo. A Fig. 17
função;
• A função de massa inicial (IMF, initial mass function), ξ
que nascem quando há formação estelar, isto é, dNestrelas
Evolução!da!população!estelar!
• O enriquecimento quı́mico do material galáctico, Z(t), qu
do tempo;
• Evolução estelar, que nos dá a evolução da temperatura
L(M,Z,t), de uma estrela de massa m e metalicidade Z (ou
no diagrama HR ao longo de sua vida). A Fig. 174 mostra
Sequência Principal.
(ex.!Starburst99!=!pacote!para!construir!
modelos!espectrofotométricos!de!star`
forming!galaxies)!
Ψ(t) = quantidade de massa convertida
em estrelas em função de tempo.
Taxa de formação estelar (SFR)
•  A!evolucão!da!população!estelar!das!galáxias!é!o!resultado!
combinado!de!diversos!fatores:!
–  Taxa!de!formação!estelar!(SFR)!
4
Sa
3
– formação!estelar!constante?!
Sb
2
Sc
– surto?!!
1
Sd
– Decaimento!exponencial,!e`t/τ!?!!!!!!!!!! 06
E/S0
4
Figura 17
estelar (un
morfológico
de formaçã
mente de f
gianti et al
2
0
6
4
Sc + surto
2
0
0
10
5
Idade [109 anos]
Poggian6!et!al.!(1999)!
Evolução!da!população!estelar!
•  A!evolucão!da!população!estelar!das!galáxias!é!o!resultado!
combinado!de!diversos!fatores:!
–  Taxa!de!formação!estelar!(SFR)!
–  A!função!de!massa!inicial!(IMF)!
Evolução!da!população!estelar!
•  A!evolucão!da!população!estelar!das!galáxias!é!o!resultado!
combinado!de!diversos!fatores:!
–  Taxa!de!formação!estelar!(SFR)!
–  A!função!de!massa!inicial!(IMF)!
–  enriquecimento!químico!do!material!galác6co:!
•  Z(t)!=!evolução!da!metalicidade!
Evolução!da!população!estelar!
•  A!evolucão!da!população!estelar!das!galáxias!é!o!resultado!
combinado!de!diversos!fatores:!
–  Taxa!de!formação!estelar!(SFR)!
–  A!função!de!massa!inicial!(IMF)!
–  enriquecimento!químico!do!material!galác6co:!
–  Evolução!estelar!=!trajetória!evolu6va!(teórica)!de!uma!estrela!!
•  Evolução!de!uma!estrela!de!massa!M!e!metalicidade!Z!em:!
•  Tef(M,Z,t)!–!temperatura!efe6va!!
•  L(M,Z,t)!–!luminosidade!
caminho!que!uma!
•  Entre!as!trajetórias!mais!utlizadas:! estrela!percorre!no!
diagrama!HR!ao!longo!
– Padova!stellar!tracks#
de!sua!vida!
– Geneva!stellar!tracks#
Sínteses!Evolu6va!de!Populações!Estelares!
•  Beatrice!Tinsley!e!depois!Gustavo!
Bruzual!foram!os!pioneros!em!
desenvolver!o!analise!de!síntese!
evolu6va!que!faz!um!“forward”!do!SED!
•  Uma!evolução!no!tempo!dos!
espectros!
!
!
!
!
!
!
Beatrice Tinsley
Gustavo Bruzual (UNAM)
Sínteses!Evolu6va!de!
Populações!Estelares!
Os!modelos!mais!
usados!são:!
!
`  Modelo!de!“surto!
único”!(single!
starburst)!de!
formação!estelar!
!
Sínteses!Evolu6va!de!
Populações!Estelares!
Os!modelos!mais!
usados!são:!
!
`  Modelo!de!“surto!
único”!(single!
starburst)!de!
formação!estelar!
!
`  Modelo!de!
formação!estelar!
exponencialmente!
decrescente!
!
Espectros!integrados!de!galáxias!
Qué!podem!dizer!
sobre!as!cores?!
An Elliptical Galaxy Spectra
• A galaxy spectrum is the sum of many stellar
spectra. If there are few blue stars the overall
shape will look red:
FEW *s
MANY *s
COMPOSITE
GALAXY
SPECTRUM
I
Blue
!
Sunday, January 23, 2011
Red
Tópicos!(Parte!I)!
1.  Revisão:!Formação!e!Evolução!Estelar!
2.  Introdução!a!Extragalác6ca!
3.  Propriedades!Gerais!das!Galáxias!
3.2.!Populações!Estelares!
•  Espectros!estelares!!
•  síntese!de!populações!estelares!
•  Distribuição!Bi`modal!de!cor!
3.3.!Função!de!Luminosidade!
4.  Propriedades!Gerais!das!Galáxias!Elíp6cas!
5.  Propriedades!Gerais!das!Galáxias!Espirais!
!
Espectros!integrados!de!galáxias!
•  As!galáxias!elíp6cas!têm!um!
espectro!dominado!por!
estrelas!vermelhas!(de!baixa!
massa)!enquanto!as!galáxias!
espirais!!têm!o!espectro!
dominado!por!estrelas!!!!!!!!!!
mais!novas.!
`  Azul!=!jovem!
`  Vermelha!=!velha!
!
Assim!de!
simples?!
Não!!!!
Sunday, January 23, 2011
Limites!dos!Modelos!
•  Limites!devido!a:!!
–  idade/ex6nção:!avermelhamento!por!poeira!ou!maior!idade?!!!
!
!
!
Limites!dos!Modelos!
•  Limites!devido!a:!!
–  idade/ex6nção!
–  idade!e!metalicidade!
•  para!uma!massa!e!idade!
específica,!uma!estrela!de!
metalicidade!menor!é!
mais!azul!(e.g.,#line#
É!fácil!dis6nguir!entre!populações!quando!só!um!dos!!
blanke?ng)!
parámetros!muda!(metalicidade!ou!idade)!
!
http://abyss.uoregon.edu/~js/lectures/st_pop/all.html
Limites!dos!Modelos!
•  Limites!devido!a:!!
–  idade/ex6nção!
–  idade!e!metalicidade!
•  para!uma!massa!e!idade!
específica,!uma!estrela!de!
metalicidade!menor!é!
mais!azul!(e.g.,#line#
blanke?ng)!
•  efeitos!similares!no!SED!
É!diucil!dis6nguir!quando!temos!que!considerar!!
•  Requer!indicadores!
efeitos!de!idade!E!metalicidade!
independentes!(e.g.,!
metalicidade,!razão!de!
linhas!de!emissão)!!
!
!
http://abyss.uoregon.edu/~js/lectures/st_pop/all.html
Limites!dos!Modelos!
•  Limites!devido!a:!!
–  idade/ex6nção!
–  idade!e!metalicidade!
–  Razões!M/L:!!
•  estrelas!de!alta!massa!possuem!um!M/L!baixo!
– a!luminosidade!destas!estrelas!pode!dominar!a!
luminosidade!íntegra!da!galáxia,!sem!que!a!massa!da!
soma!destas!estrelas!seja!representa6va!da!massa!
total!da!galáxia!(ex.!thermally3pulsa?ng#AGB;!TP`AGB)!
•  Se!não!consideramos!isso!e!assumimos!que!toda!a!
luminosidade!observada!é!devido!à!estrelas!normais!(de!
baixa!massa),!o!modelos!sobre`es6marão!a!massa!estelar!
total!da!galáxia.!
–  Isso!é!par6cularmente!crí6co!no!caso!de!galáxias!starburst!
(com!TP`AGBs!em!rela6va!abundância)!
Limites!dos!Modelos!
•  Limites!devido!a:!!
–  idade/ex6nção!
–  idade!e!metalicidade!
–  Razões!M/L!
–  Fases!estelares!pouco!conhecidas!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
(com!baixa!representação!nos!espectros!estelares)!
•  “Blue!stragglers”!!
–  Contaminação!nas!linhas!de!
emissão!(Balmer)!de!sistemas!
estelares!não!resolvidos!!!
subes6mação!das!idades!
estelares!
Presença!de!hidrogênio!adicional!
prolonga!a!fusão!nuclear!(estadia!
na!SP!é!prolongada).!Fontes?!
'
•  !intercâmbio!de!material!num!
sistema!binario!ou!merger!deste!
mesmo.!
•  Convecção/dragado!leva!
hidrogênio!nas!camadas!
externas!até!o!centro!da!estrela!
Limites!dos!Modelos!
•  Limites!devido!a:!!
–  idade/ex6nção!
–  idade!e!metalicidade!
–  Razões!M/L!
–  Fases!estelares!pouco!conhecidas!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
(com!baixa!representação!nos!espectros!estelares)!
•  “Blue!stragglers”!!
•  Estrelas!TP`AGB!(fase!pulsa6va!das!estrelas!AGB)!!
– contribuem!~50%!dos!metais!e!afetam!muito!o!
espectro!integrado!(no!IV!próximo)!de!pop.!estelares!
de!0.1`10Gyr!
– Temos!pouca!informação!desta!fase!!!bibliotecas!
empíricas!tem!as!suas!falhas!também.!
Bimodalidades!em!propriedades!
integradas!de!galáxias!
Baldry et al. 2004
•  Bimodalidade!em!cor!
–  Distribuição!bi`modal!nas!côres!de!
galáxias!SDSS!(z~0)!
•  Red!clump!
•  Blue!cloud!
–  Região!“menos!povoada”:!!!
•  valhe#verde#
#
#
Magnitude em R
Bimodalidades!em!propriedades!
integradas!de!galáxias!
#
z~
0.1-0.2
Wyder!et!al.!(2007)!
•  Bimodalidade!em!cor!
–  Distribuição!bi`modal!nas!côres!de!
galáxias!SDSS!(z~0)!
•  Red!clump!
•  Blue!cloud!
–  Região!“vazía”:!!valhe#verde#
–  A!distribuição!bimodal!se!estende!
até!redshiÖs!maiores.!
!
•  Bimodalidade!em!cor!
–  Distribuição!bi`modal!nas!côres!de!
galáxias!SDSS!(z~0)!
•  Red!clump!
•  Blue!cloud!
–  Região!“vazía”:!!valhe#verde#
–  A!distribuição!bimodal!se!estende!
até!redshiÖs!maiores.!
–  SFH!varia!bastante,!mas!podemos!
classificar!em!termos!gerais:!
•  Galáxias!“a6vas”!e!“passivas”!
–  Evolução!vermelhas!!!azuis!
Martin, D. C., et al.
Bimodalidades!em!propriedades!
integradas!de!galáxias!