2ª Lista de exercícios do 2º ano do E.M. – 1º bimestre.
Física A – Prof. Marco Antônio
COLISÕES E ÁTOMO
1. Um átomo de Hélio, com velocidade inicial de 1000 m/s colide com outro átomo de Hélio, inicialmente em
repouso. Considerando que o choque foi perfeitamente elástico e que a velocidade de ambos tem sempre
mesma direção e sentido, calcule a velocidade dos dois átomos após o choque.
R: 0 e 1000m/s.
2. Dois patinadores de mesma massa deslocam-se numa trajetória retilínea com velocidades
respectivamente iguais a 8m/s e 6 m/s. O patinador mais rápido persegue o outro. Ao alcançá-lo, salta
verticalmente e agarra-se às suas costas, passando os dois a se deslocarem com a mesma velocidade V.
Calcule V.
R: 7 m/s
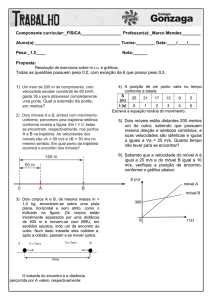
3. Ao longo de um eixo x, uma partícula A de massa 0,1kg incide com velocidade escalar de 2 m/s sobre
uma partícula B de massa 0,3 kg, inicialmente em repouso. O esquema a seguir ilustra isso, como também
o que sucede após o choque.
a) Mostre que houve conservação da quantidade de movimento do sistema.
b) Calcule o coeficiente de restituição dessa colisão e, a seguir, informe se houve ou não perda de energia
mecânica do sistema nessa colisão.
4. Sobre uma superfície lisa e horizontal, ocorre um choque central de um corpo X, de massa M e
velocidade 6 m/s, com outro corpo Y de massa 2M que estava parado. Após o choque, o corpo X retrocede
com velocidade de 2 m/s, determine a velocidade que o corpo Y avança.
R: 4m/s
5. O gráfico abaixo representa as velocidades escalares de duas pequenas esferas, A e B, que realizam
uma colisão frontal (com faixa de duração em destaque no gráfico).
Determine:
a) O coeficiente de restituição entre A e B.
b) A relação entre as massas de A e B.
6. Dois corpos A e B, de massa respectivamente iguais a 2 kg e 6 kg, movimentam-se sobre uma
mesma trajetória retilínea, no mesmo sentido com velocidades vA = 4 m/s e vB = 1 m/s, onde o
atrito é desprezível. Sabendo-se que os corpos realizam uma colisão perfeitamente elástica,
determine suas velocidades após o choque.
R: v'A = 0,5 m/s e v'B = 2,5 m/s.
7. Determine o coeficiente de restituição dos seguintes choques:
a)
antes
1
depois
10m/s
2
2m/s
1
10m/s
2m/s
2
b)
antes
1
6m/s
depois
6m/s
4m/s
2
1
2
4m/s
c)
antes
1
5m/s
depois
2
1m/s
1
2m/s
2
d)
antes
1
10m/s
depois
2
4m/s
1m/s
1
2
5m/s
e)
antes
1
2m/s
depois
2m/s
2
1
2
8. Um carro de 800 kg, parado num sinal vermelho, é abalroado por trás por outro carro, de 1200
kg, com velocidade de 72 km/h. Imediatamente após o choque, os dois carros se movem juntos.
a)
calcule
a
velocidade
do
conjunto
logo
após
a
colisão;
b) Prove que o choque não é elástico.
R:a)12m/s;
b) utilize a energia cinética inicial e final e verifique que a energia cinética inicial é maior
que a energia cinética final e há o fato dos corpos caminharem juntos após o choque
comprovando que é um choque inelástico
9. (UERJ 2006) Duas esferas, A e B, deslocam-se sobre uma mesa conforme mostra a figura 1.
Quando as esferas A e B atingem velocidades de 8 m/s e 1 m/s, respectivamente, ocorre uma
colisão perfeitamente inelástica entre ambas.
O gráfico na figura 2 relaciona o momento linear Q, em kg × m/s, e a velocidade , em m/s, de cada
esfera antes da colisão.
R: a) 1 .
b) 0,66.
c) 0.
d) 1.
e) 0.
Após a colisão, as esferas adquirem a velocidade, em m/s, equivalente a:
a) 8,8
b) 6,2
c) 3,0
d) 2,1
e) 5,0
10. Uma bola é solta de uma altura H = 100 m. Ela choca-se com o solo, e atinge na volta, uma altura
máxima de 64 m. Sabendo que a aceleração da gravidade é g = 10 m/s², calcular o coeficiente de
restituição.
R: e = 0,8
11. Uma bola de borracha de 0,2 kg cai, a partir do repouso, de uma altura H = 1,6 m e, após o choque
frontal com o solo, retorna até uma altura máxima h = 0,4 m. Adotando g = 10 m/s² e desprezando a
resistência do ar, determine:
a) a perda de energia mecânica da bola nesse choque;
b) o coeficiente de restituição no choque.
R: a) 2,4 J
b) 0,5
12. Uma esfera A de massa igual a 2 kg desloca-se numa superfície horizontal, sem atrito, com
velocidade de 3 m/s, e atinge frontalmente uma segunda esfera, B, de massa m, inicialmente em
repouso. Após o choque, perfeitamente elástico, a esfera A recua com velocidade de 1 m/s.
Determine:
a) o valor da massa m da esfera B;
b) a energia cinética da esfera B, após o choque.
R:a)4kg;
b) 8 J.
13. O átomo de um certo elemento é composto por 2 prótons, 2 nêutrons e 2 elétrons.
Determine a carga elétrica do núcleo deste átomo.
R: Q = 3,2 . 10-19C
14. (UNESP) De acordo com o modelo atômico atual, os prótons e nêutrons não são mais considerados
partículas elementares. Eles seriam formados de três partículas ainda menores, os quarks. Admite-se a
existência de 12 quarks na natureza, mas só dois tipos formam os prótons e nêutrons, o quark up (u), de
carga elétrica positiva, igual a 2/3 do valor da carga do elétron, e o quark down (d), de carga elétrica negativa,
igual a 1/3 do valor da carga do elétron. A partir dessas informações, assinale a alternativa que apresenta
corretamente a composição do próton e do nêutron.
� (I) Próton.
� (II) Nêutron.
a) (I) d, d, d, (II) u, u, u
b) (I) d, d, u, (II) u, u, d
c) (I) d, u, u, (II) u, d, d
d) (I) u, u, u, (II) d, d, d
e) (I) d, d, d, (II) d, d, d
15. Sabe-se que a carga do elétron vale -1,6 x 10-19 C. Considere-se um bastão de vidro que foi atritado e
perdeu elétrons, ficando positivamente carregado com a carga de 5,0 x 10-6 C. Conclui-se que o número de
elétrons retirados do bastão foi de aproximadamente:
a)
1,6 x 1016
b)
3,1 x 1011
c)
2,5 x 1010
d)
3,1 x 1013
e)
1,6 x 1015
16. Um corpo está eletrizado com uma carga negativa de 1,6 x 10-6 C. Sabe-se que a carga do elétron é 1,6 x
10-19 C, pode-se afirmar que esse corpo tem um excesso de elétrons da ordem de
a)
1025
b)
1013
c)
1010
d)
10-13
e)
10-25