IF-UFRJ Elementos de Eletrônica Analógica Mestrado Profisssional

IF-UFRJ
Elementos de Eletrônica Analógica
Mestrado Profisssional em Ensino de Física
Prof. Antônio Carlos Santos
Aula 4: Diodos
Este material foi baseado em livros e manuais existentes
na literatura (vide referências)
e na internet e foi
confeccionado exclusivamente para uso como nota de
aula para as práticas de Laboratório de Física Moderna
Eletrônica. Pela forma rápida que foi confeccionado,
algumas partes foram extraídas quase verbatim de outros
autores citados na lista de referências. Trata-se de um
texto em processo de constante modificação. Por
gentileza, me informe os erros que encontrar.
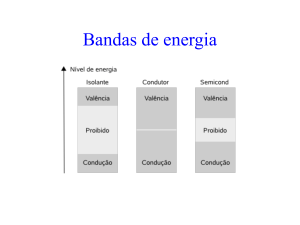
Teoria de bandas em sólidos
Os elétrons em um átomo isolado ocupam orbitais atômicos, que forma um conjunto discreto de níveis de energia. Se
vários átomos são postos lado a lado, formando uma molécula, seus ortbitais atômicos se dividem, com osciladores
acoplados. Isto produz um número de orbitais moleculares proporcional ao número de átomos. Quando um grande
20
número de átomos ( da ordem de 10 ou mais) são juntados formando um sólido, o número de orbitais torna-se
excessivamente elevado. Em conseqüência, a diferença em energia entre eles torna-se muito pequena. Assim, em
sólidos, os níveis de energia formam bandas contínuas. No entanto, alguns intervalos de energia não contém nenhum
orbital, formando intervalos (gaps).
Introdução, semicondutores, Tipos de Diodo
Os diferentes materiais podem ser caracterizados, de forma ampla, como condutores, semicondutores e isolantes, de
acordo com a sua maior ou menor resistência à passagem da corrente elétrica.
-5
-8
10
16
Os valores da resistividade variam de 10 a 10 Ωm para condutores, até 10 a 10 Ωm para dielétricos. Os
-6
5
semicondutores caracterizam-se por uma resistividade variável na faixa de 10 a 10 Ωm, dependendo do material e da
temperatura.
19
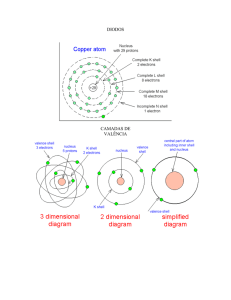
Semicondutor intrínseco :
Num semicondutor puro (ou intrínseco) como o Ge, ou Si, que possuem valência 4, em seu estado sólido
(cristalino) cada átomo se encontra cercado de 4 átomos vizinhos, com seus elétrons partilhados entre dois átomos,
numa ligação covalente formando pares. A baixa temperatura estes elétrons estão fixos aos átomos que os
compartilham, resultando assim que o semicondutor não apresenta portadores móveis de carga comportando-se,
portanto, como isolante. Aumentando a temperatura estes elétrons podem adquirir energia suficiente para romper esta
ligação covalente, liberando-se dos átomos e tornando-se portadores livres no corpo do cristal, hábeis, portanto, para
reagir a um campo elétrico externo, conduzindo corrente.
Fig. 3.1 – Um semicondutor intrínseco
Ao mesmo tempo, quando um elétron é liberado de sua posição original, forma-se uma lacuna de carga no
corpo do cristal. Como o átomo era inicialmente neutro, forma-se uma lacuna (buraco) de carga positiva na posição
originalmente ocupada pelo elétron liberado. A lacuna pode ser preenchida por um outro elétron liberado de um átomo
vizinho. Esta nova lacuna, da mesma forma, pode ser preenchida por um elétron liberado de um outro átomo, e assim
sucessivamente num processo caótico.
Desta forma, se observamos apenas o buraco de carga positiva, vemo-lo se mover pelo cristal de forma
aleatória, como faria uma carga livre. Podemos então dizer que o buraco se comporta com um portador de carga
positivo.
É claro que, sob a ação de um campo elétrico externo aplicado ao cristal, este movimento se ordena,
resultando numa corrente elétrica portada pelos buracos de forma inteiramente similar àquela portada por elétrons
livres. Assim podemos dizer que com o aumento da temperatura o semicondutor apresentará um número cada vez
maior de pares elétrons-buraco criados, ou seja, de portadores de carga positivos (buracos) e negativos (elétrons)
variando assim a sua resistividade. A corrente elétrica total será a soma da corrente provocada pelos elétrons se
movendo em sentido contrário ao do campo elétrico e dos buracos se movendo no sentido do campo. Temos assim o
que é chamada a condução intrínseca do semicondutor e a condutibilidade (inverso da resistividade) a ela associada
chamamos condutividade intrínseca.
Semicondutor extrínseco:
20
Se adicionarmos a um semicondutor, por exemplo o Ge, que tem valência 4, quando em estado líquido (derretido), uma
ínfima quantidade de um outro elemento, por exemplo, o As (valência 5), ao solidificar-se, o cristal resultante será
essencialmente o de Ge, com alguns átomos de As tomando o lugar, na estrutura cristalina, de átomos de Ge.
Como o As tem valência 5 e todos os átomos circundantes, de Ge, têm valência 4, haverá um elétron do As
que estará muito fracamente ligado, de tal modo que, em baixas temperaturas (ambiente) este elétron estará livre com
resultado da excitação térmica. Assim, este cristal de Ge, “dopado” com As, terá um excesso de portadores negativos
(elétrons), adicionalmente àqueles portadores resultantes dos pares elétron-buraco que já discutimos. Note que o cristal
como um todo continua a ter carga total zero. Estes elétrons livres podem assim reagir a uma campo elétrico externo,
tal como ocorre num metal, tornando-se fundamentalmente responsáveis pela condutibilidade elétrica do cristal.
Chamamos este cristal, agora impuro com As, de semicondutor do tipo n devido ao excesso de portadores de carga
negativa.
Da mesma forma podemos dopar um cristal de Ge com uma impureza de valência 3,por exemplo o Ga. Neste
caso, teremos a falta de um elétron em cada centro cristalino em que se encontre o um átomo de Ga.
A
B
Fig. 3.2 – Semicondutores extrínsecos: A) tipo n; B) tipo p
Temos então uma lacuna que será preenchida por um elétron de um átomo de Ge que ao cedê-lo terá uma
carga positiva.
Como descrito anteriormente, este buraco poderá deslocar-se pelo cristal, caoticamente, ou ordenadamente
caso seja aplicado um campo elétrico, resultando numa condução do tipo p, positiva. A este cristal chamamos
semicondutor do tipo p.
Assim podemos dizer que num semicondutor do tipo p (n) os buracos (elétrons) são os portadores de carga
majoritários e os elétrons (buracos) os minoritários.
Em baixas temperaturas os portadores minoritários têm pouca influência na condutibilidade total. Contudo, em
temperaturas mais altas um semicondutor do tipo p, ou n, terá uma condução mista.
Consideremos um cristal de Ge do tipo p (tipo n); se aplicarmos uma diferença de potencial a este cristal,
observaremos que os portadores majoritários, que são os buracos no tipo p (elétrons no tipo n) se movimentarão no
sentido do campo (contrário ao do campo) e os minoritários, que são os elétrons no tipo p (buracos no tipo n) no sentido
contrário ao do campo (sentido do campo) estabelecendo-se uma corrente elétrica. Assim o semicondutor dopado se
comportará como um condutor razoável.
Junção semicondutora pn
Consideremos um semicondutor dopado diversamente em duas regiões, uma do tipo p e outra do tipo n. Observemos a
dinâmica que se estabelece com os portadores de carga na junção destas duas camadas (figura abaixo).
Consideremos o instante da junção: a parte do tipo p, que é neutra, contém um excesso de buracos e a do tipo n
(também neutra) um excesso de elétrons. Por difusão, pelo seu movimento térmico (aleatório), buracos migrarão de p
para n e elétrons migrarão de n para p. Após algum tempo, devido a esta migração, haverá um excesso de cargas
negativas na região p e um excesso de cargas positivas na região n.
21
Estabelece-se um campo elétrico numa faixa em torno da junção que leva a reduzir (ou cessar) a migração dos
portadores majoritários de p para n (buracos) e de n para p (elétrons).
Agora somente aqueles buracos da região p ou elétrons da região n que tiverem energia cinética suficiente para
ultrapassar a barreira de potencial poderão migrar (aumentando ainda mais a barreira e tendendo a fazer cessar o fluxo
de portadores majoritários)
No entanto, em função de seu movimento caótico no interior do cristal, os portadores minoritários poderão se aproximar
da junção e serem assim “puxados” pelo campo elétrico já estabelecido através da junção para a outra região.
O campo elétrico estabelecido pelos portadores majoritários facilitará a difusão, de uma região para outra, dos
portadores minoritários. Os fluxos de difusão em ambos os sentidos terá resultante nula. Assim, sem a presença de um
campo externo, a corrente total através da faixa de transição (região de depleção) é zero. Note que no equilíbrio,
praticamente não haverá portadores móveis na região de depleção, pois estes são acelerados pelo campo elétrico,
restando apenas os íons da rede cristalina,o que resulta ser esta região de baixa condutividade. No restante do cristal,
tanto na região n quanto na região p, continuamos a ter portadores (móveis) de carga, tanto majoritários quanto
minoritários, tendo estas regiões alta condutividade. Assim, se for aplicado um campo elétrico a esta junção de
semicondutores, tudo se passará como se esta diferença de potencial estivesse aplicada diretamente à região de
depleção que contém a junção.
O diodo semicondutor
Até a aula passada, estudamos apenas componentes lineares, ou seja, que apresentam uma relação linear entre a
tensão aplicada e a corrente. A junção semicondutora estudada acima, pela suas características de resposta à
aplicação de um campo elétrico externo, é chamada diodo. Um estudo detalhado de um diodo nos mostra que,
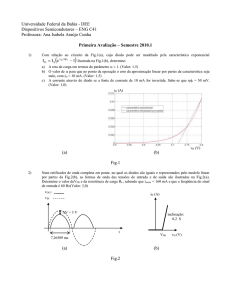
conservando a temperatura constante, a variação da corrente com a tensão aplicada segue uma lei exponencial da
forma:
 eV

I = I o  e kT − 1


22
Fig. 3.5 – Característica volt-ampere do diodo.
Onde V é a tensão aplicada ao diodo, Io é a corrente reversa de saturação, ou corrente intrínseca (valor de I quando V é
negativo e grande, ou seja, tensão reversa grande) k é a constante de Boltzman e T é a temperatura em Kelvin.
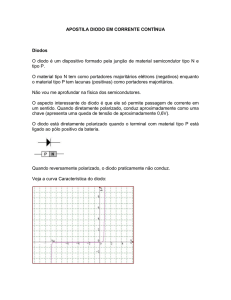
O diodo é um elemento não linear básico, porém muito importante que possui dois terminais, o anodo e o catodo. O
diodo é convencionalmente indicado num circuito por uma seta e um traço vertical (vide figura abaixo). O sentido da
seta indica o sentido da corrente direta.
O diodo ideal (primeira aproximação para o diodo)– o termo ideal refere-se a qualquer componente que possui
características ideais (perfeito!). O diodo ideal é um componente com dois terminais e que conduz corrente em uma
direção (do anodo para o catodo, no sentido convencional da corrente) e que atua como um circuito aberto para
correntes no sentido oposto. O diodo ideal é um curto-circuito na sua região de condução, ou seja, possui resistência
nula se a tensão no anodo for maior do que a do catodo. Se a tensão no catodo for maior do que a do anodo, o diodo
possui resistência infinita. Note que o diodo ideal, como o próprio nome diz, é uma idealização.
Segunda aproximação para o diodo- Algumas vezes desejamos um modelo mais preciso do que a hipótese do diodo
ideal, mas ainda não queremos utilizar equações não lineares. Então podemos utilizar modelos que cada vez mais
realistas. Na segunda aproximação para o diodo, o diodo conduzirá se a diferença de potencial entre o anodo e o
catodo seja igual ou superior a 0,7 V.
Terceira aproximaçãointerna.
Na terceira aproximação (aproximação linear por partes) é acrescentada uma resistência
23
Um parâmetro importante é a potência máxima dissipada PDmáx = VDID , onde VD é a tensão aplicada ao diodo e ID a
corrente que o atravessa. Na maioria dos casos que trataremos aqui, VD ≅ 0,7 V, então PDmáx = 0,7ID
Reta de carga - Considerando-se um circuito simples com dois componentes passivos em série e uma fonte de tensão
contínua, como o da figura abaixo, indaga-se como a tensão da fonte irá se distribuir entre os outros dois
componentes. Uma saída seria usar um dos modelos simples acima para o diodo (primeira, segunda ou terceira
aproximação). Mas, se conhecemos a curva característica de do diodo I=I(V), podemos aplicá-la para determinar a
divisão de tensão. Aplicando a lei das malhas: V + VD + VR = 0, como VR = -RI e VD é a curva típica do diodo, podemos
resolver esta equação (não linear) graficamente. O problema consiste em localizar o ponto comum, ou interseção, das
curvas (equações) acima. Apresentamos o resultado no gráfico ID versus VD, onde a lei das malhas é representada pro
uma reta que passa pelos pontos (V,0) e (0,V/R). Esta reta recebe o nome de reta de carga, sendo a carga, no caso, o
resistor R.
Tipos de diodo
Diodo retificador – É o diodo próprio para trabalhar com
altas correntes (acima de 1 A). Normalmente tem o
corpo preto com um anel cinza nas extremidades
Diodo de sinal - É o diodo fabricado para trabalhar com baixa correntes (na faixa dos mA).
Tem geralmente o corpo de vidro, é menor e tem os terminais mais finos que o diodo
retificador.
Diodo de germânio – tem o corpo de vidro transparente e era usado nos rádios antigos
para demodular os sinais de AM e FM (transformar um sinal de alta freqüência (RF) num
de baixa (áudio)).
24
LED (Light Emitting Diode) – É um diodo que quando convenientemente
polarizado emite luz. Sua funcionalidade básica é a emissão de luz em
locais e instrumentos onde se torna mais conveniente a sua utilização no
lugar de uma lâmpada. Especialmente utilizado em produtos de
microeletrônica como sinalizador de avisos, também pode ser encontrado
em tamanho maior, como em alguns modelos de semáfos.
Fotodiodo – é um fotodetector, ou seja, serve para
detectar luz visível, ultra-violeta ou raios-x. Utilizado
na polarização direta, produz uma corrente quando
luz incide sobre ele pelo efeito fotoelétrico. Um
exemplo são os utilizados nas calculadoras solares.
Na polarização reversa, pode atuar como detector de
luz. A sua resistência em polarização reversa é muito
alta, mais diminui com a incidência de luz (LDR ou
Light depending resistor) O LDR é muito
frequentemente utilizado nas chamadas fotocélulas
que controlam o acendimento de poste de
iluminação e luzes em residências. Também é
utilizado em sensores foto-elétricos assim como fotodiodos
LDR
Testes de diodos com multímetro digital – Para diodos e transistores em geral usamos o multímetro digital na escala
marcada com um símbolo de diodo. A seguir medimos a peça nos dois sentidos. Se ele indicar baixa resistência num
sentido (entre 400 e 900 Ω) e infinita no outro, o diodo estará bom.
Parte prática
Material Experimental
Gerador de sinais
Osciloscópio
Fonte variável
Diodo
Resistores de 1 kΩ, 10 kΩ e 100 kΩ
I – Levantamento da curva do diodo
1 – Meça com um ohmímetro a resistência direta e reversa do diodo.
Resistência direta
Resistência reversa
2- Monte o circuito da figura abaixo
25
Tensão (V)
Corrente (mA)
3- Inverta a polaridade do diodo e repita o item anterior
Tensão (V)
Corrente (mA)
corrente (mA)
4- Faça um gráfico corrente versus tensa com os dados obtidos
tensão (V)
Referências
[1] Laboratório de Eletricidade e Eletrônica , F. G. Capuano e M. A. M. Marino. Ed. Érica
[2] David. E. LaLond e John A. Ross, Dispositivos e Circuitos Eletrônicos Vol. 1, Makron Books.
[3] Roteiro de Fisica Experimental IV (UFRJ)
26
Lista de exercícios para casa
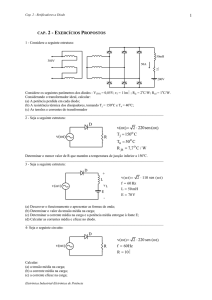
1-
Encontre os valores de corrente (I) e tensão (V) para os circuitos abaixo, considerando os diodos como ideais
(segunda aproximação).
A
B
C
D
27