F - Anjo Albuquerque

Tipos de Forças
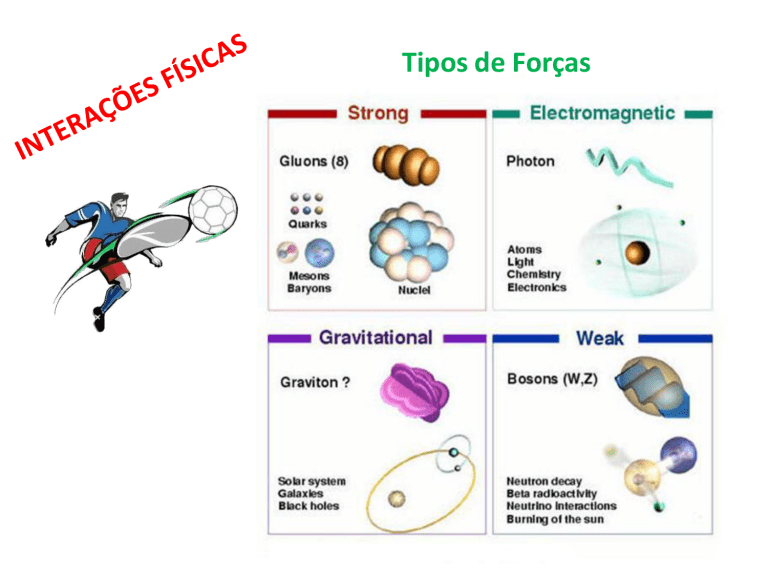
Tipos de forças fundamentais na Natureza
Existem quatro tipos de interações/forças fundamentais na Natureza que
atuam entre partículas a uma certa distância umas das outras:
 Gravitacional – força que os corpos com massa exercem uns sobre os outros.
Como é muito fraca é necessário ter pelo menos uma massa muito grande,
como a de um planeta, para que se possa detetar o seu efeito.
 Eletromagnética – força elétrica, que as cargas elétricas exercem umas sobre
as outras; - força magnética, que as correntes elétricas ou ímanes exercem uns
sobre os outros.
 Nuclear forte – responsável pela estabilidade nuclear, ou seja, a força que
une protões e neutrões no interior do núcleo.
 Nuclear fraca – responsável pela transformação de certos núcleos em que um
neutrão se transforma num protão, ou vice-versa (radioatividade)
Interação entre corpos. O que significa?
• Uma interação entre dois ou mais corpos significa uma ação
reciproca entre eles.
• Uma interação entre corpos pode conduzir à alteração do estado de
repouso, ou de movimento de um corpo e/ou produzir deformação.
• Podem ocorrer por contato ou à distância.
As interações, em Física
Na realidade, mesmo as interações por contacto são “interações à
distância” dado que não ocorre contacto entre os átomos dos corpos
que interagem, pois eles, átomos, interagem à distância!
Em Física, as interações entre os corpos são explicadas através
do conceito de força.
Força de contato: o corpo sobre o qual é exercida a força está em
contato físico com o corpo que exerce a força; quando deixa de haver
contato cessa a interação.
FA / P

FP / A
Na figura,
 a pedra exerce uma força de contato sobre a
areia, FP / A , e a areia exerce uma força de contato sobre

a pedra FA / P
Gravitacional
eletromagnética
Nuclear forte
Nuclear fraca
n
p+e+
10-15 m
10-16 m
Alcance
Infinito
Infinito
Interação
Entre todas as
massas
Entre todas as
cargas elétricas
Efeito
Atração entre
massas
Atração e
repulsão entre
cargas elétricas
Intensidade
relativa
10-40
10-2
(dimensão núcleo)
Entre quarks
Entre nucleões
e eletrões
Estabilidade
nuclear
Decaimento
beta
1
10-5
3ª Lei de Newton
Lei da ação - reação
Se uma força resulta
da interação entre
dois corpos, então
não existem forças
isoladas.
As forças
atuam sempre
aos pares.
3ª Lei de Newton, ou Lei da ação - reação
• Os gases de escape exercem uma força vertical e
ascendente sobre o foguetão, e este sobe.
• O foguetão exerce uma força vertical e descendente sobre
os gases de escape, e estes descem.
Estas duas forças têm a mesma intensidade e são simétricas
tal que:
Terceira Lei de Newton:
Quando um corpo exerce uma força sobre outro, este exerce também sobre o
primeiro uma força de igual módulo e direção, mas de sentido contrário, ou


seja
FA / B   FB / A

FA / B é a força que o corpo A
exerce sobre o corpo B.

FB / A é a força que o corpo B
exerce sobre o corpo A.
Forças que não constituem um par
ação - reação
 
As forças N e P não constituem
um par ação – reação porque
são forças aplicadas no mesmo
corpo, e por isso os seus
efeitos anulam-se.
As forças que atuam na maçã:
• a reação normal, que resulta da interação
de contato entre a mesa e a maçã;
• o peso, que resulta da interação gravítica, à
distância, entre a Terra e a maçã.
As forças de um par ação - reação
As forças de um par ação - reação


É par ação – reação: N e N ´

A reação normal N é a força que a
mesa exerce
 a maçã; o seu par é
 sobre
a força N ´= - N que a maçã exerce
sobre a mesa, de direção vertical ,
sentido para baixo e intensidade igual à
da reação normal.
 
É par ação – reação: P e P´

O peso P é a força gravítica que a Terra
 exerce

sobre a maçã e o seu par é a força P´ = - P que a
maçã exerce sobre a Terra, de direção vertical,
sentido para cima e intensidade igual à do peso.
Características das forças do par
ação - reação
• Têm o mesmo módulo e direção;
• Têm sentidos opostos;
• Atuam em corpos diferentes, por isso os seus efeitos não
se anulam;
• Resultam da mesma interação.
Lei da Gravitação Universal de Newton
Todos os corpos no Universo, por terem massa, exercem forças de
atração gravítica uns sobre os outros.

F`

F
r
• O corpo de massa M atrai o
corpo de massa m com uma

força F
• O corpo de massa m atrai o
corpo de massa M com uma

força F `
• As duas forças constituem


par ação-reação: F = - F `
Lei da Gravitação Universal de Newton
Lei da Gravitação Universal – dois corpos atraem-se exercendo,
um sobre o outro, uma força que é diretamente proporcional às
suas massas e inversamente proporcional ao quadrado da
distância que os separa.
Expressão matemática da Lei
G é a constante de gravitação universal e vale, em qualquer
lugar do Universo, 6.67 x 10-11 N⋅m2 / kg2
g, é a aceleração devido à gravidade e vale 9.80 m/s2 à superfície da Terra e varia com a
localização
Lei da Gravitação Universal de Newton
MT m
MT m
PG 2 G
r
( RT  h) 2
sites.google.com/site/.../peso massa
O peso de um corpo de massa m a uma
altitude h é a força gravitacional que o
planeta Terra, de massa MT e raio RT, exerce
nesse corpo que se encontra a uma distância
r = RT + h do centro da Terra.
sites.google.com/site/.../peso_massa
Peso de um corpo nos planetas do
Sistema Solar
Efeito das forças sobre a velocidade
A ação de uma força, ou de um sistema de forças, de resultante não
nula, altera a velocidade de um corpo, quer em módulo, quer em
direção, quer em sentido.
Assim:
1- se a velocidade do corpo é nula, a força aplicada faz mover o corpo
assim que superar a força de atrito.
Efeito das forças sobre a velocidade
2- se a força tem a direção da velocidade, ela só faz variar o módulo da
velocidade, mas não a direção desta.
 Se tiver o sentido da velocidade, faz aumentar a velocidade do
corpo.
 Se tiver o sentido oposto da velocidade, faz diminuir a
velocidade do corpo.
sendo, por isso mesmo, um movimento retilíneo.
Efeito das forças sobre a velocidade
3- se a força não tiver a direção da velocidade, faz mudar a direção da
velocidade e o movimento é curvilíneo.
Neste caso, decompõe-se a força segundo duas direções:

 Na direção da velocidade (componente tangencial), Fx ,
que faz variar o módulo da velocidade.
 Na direção perpendicular à velocidade

(componente normal), F y , que faz
mudar a direção da velocidade.
Efeito das forças sobre a velocidade
3- se a força não tiver a direção da velocidade, faz mudar a direção da
velocidade e o movimento é curvilíneo.
Consideremos o lançamento horizontal de um corpo próximo da superfície da
Terra.
Dependendo da velocidade horizontal, paralela à superfície…
Para uma
velocidade de
lançamento
suficientemente
grande o corpo
entrará em órbita!
A velocidade é um vetor tangente à trajetória.
Efeito das forças sobre a velocidade
Sempre que num corpo atuar uma
força constante e perpendicular à
velocidade a direção do movimento
varia, mas o módulo da velocidade
permanece constante.
Se a Lua partisse da atual posição que ocupa com velocidade nula, colidiria
com a Terra, devido à força gravitacional que a Terra exerce sobre ela.
A Lua exerce sobre a Terra uma força gravitacional de igual intensidade.
Porém a sua massa é cerca de 81 vezes menor que a da Terra.
Por isso a Lua cairia sobre a Terra e não o contrário.
No movimento retilíneo vimos
Aceleração média – variação da velocidade por unidade de tempo:


v
aceleração média  a m 
t
Unidade SI: m s-2

aceleração média, am , é uma grandeza vetorial:
• direção – a do movimento (aceleração e velocidade são paralelas)
• Sentido – positivo ou negativo
• componente escalar a  v
m
t
No movimento retilíneo vimos
Movimento com aceleração positiva Movimento com aceleração negativa
(a aceleração aponta no sentido do movimento)
(a aceleração aponta no sentido oposto do
movimento)


am e v


am e v
possuem a mesma direção e sentido.
possuem sentidos contrários.
movimento retilíneo acelerado movimento retilíneo retardado
a>0 e v>0 ou a<0 e v<0
a>0 e v<0 ou a<0 e v>0
Nos movimentos curvilíneos
Nos movimentos curvilíneos a aceleração existe sempre mesmo que

o módulo da velocidade não varie, pois a direção de v varia sempre.

No movimento curvilíneo a velocidade, v , e a variação da velocidade,

v , não têm a mesma direção.
Determinação gráfica da aceleração
A aceleração num determinado instante pode ser calculada a
partir do declive da tangente ao gráfico velocidade – tempo no
instante pretendido.
Informação do gráfico v=f(t):
• O valor algébrico da velocidade em cada instante;
• O sentido da velocidade (no sentido positivo do
eixo escolhido ou no sentido contrário);
• O valor algébrico do deslocamento (dado pela
“área” subentendida pela curva do gráfico
relativamente à reta de equação v=0);
• O valor algébrico da aceleração.
Determinação gráfica da aceleração
a<0
a>0
a=0
Gráfico velocidade – tempo de um movimento retilíneo
Segunda Lei de Newton

FR

FR

FR
Conclusão: para um determinado corpo, a resultante das forças, ou
força resultante, FR , tem sempre a mesma direção e sentido da

aceleração, a, do seu centro de massa.
O módulo da força resultante é diretamente proporcional ao módulo da
sua aceleração.
Segunda Lei de Newton
ou Lei Fundamental da Dinâmica
O módulo da força resultante que atua sobre um corpo de massa
constante é diretamente proporcional ao módulo da aceleração que
ele adquire, sendo a constante de proporcionalidade igual à massa
inercial.


FR  ma

FR - força resultante (N) que atua no corpo
m - massa inercial (é uma propriedade de cada corpo) (Kg)

a - aceleração adquirida pelo corpo (ms-2)
Segunda Lei de Newton
Três blocos com massas diferentes são sujeitos à mesma força resultante:
Conclusão: quanto maior for a massa do corpo, menor será a aceleração
adquirida para uma determinada força resultante, ou seja, maior será a
sua inércia (tendência para manter a mesma velocidade)
m3 < m 1 < m 2



a3  a1  a2
Caracterizar o movimento
Movimento
retilíneo
(a direção da
velocidade é
constante)
Movimento
curvilíneo
(a direção da
velocidade
varia)
 
 
F 0a 0
 
 
F 0a0


FR e v paralelos
 
 
F 0a0
 
FR e v nunca
são paralelos
 
aev
variado
paralelos
 
aev
Acelerado
 
 a e v têm o mesmo sentido
Retardado
 
 a e v têm o sentidos opostos
Uniforme
nunca são
paralelos

v
Uniforme
variado
 a e v têm o mesmo sin al
 a e v têm sin ais contrários

• Fae v são perpendicu lares
 
e v têm o mesmo sentido
• am
R
acelerado
• ângulo entre a e v menor que 900
retardado
• ângulo entre a e v maior que 900
Lei da inércia
Conclusão:
Objetos em repouso tendem a permanecer
em repouso a menos que sobre eles
atue um conjunto de forças cuja resultante
seja diferente de zero
Aristóteles explica…
Para manter um corpo em movimento é
necessário que atue uma força sobre ele.
Nota: nesta época não se conhecia o atrito.
Galileu explica…
Se a resultante das forças que atuam sobre
um corpo for nula, a sua velocidade
permanecerá constante.
Galileu imaginou uma situação ideal em
que um corpo deslizava numa
superfície horizontal sem atrito.
Será que a esfera vai parar?
• A força resultante é nula
o movimento não pode ser acelerado
nem retardado; A velocidade da esfera será constante (movimento
retilíneo uniforme)
Newton explica…
Se a força resultante que atua sobre um corpo for
nula, o corpo permanecerá em repouso se estiver
inicialmente em repouso, ou terá movimento retilíneo
uniforme se estiver em movimento.
Quando a resultante das forças que atua sobre um corpo é nula:
• Se o corpo estiver inicialmente em repouso, permanecerá em
repouso (
);
• Se o corpo estiver inicialmente em movimento, permanecerá
com a mesma velocidade, ou seja, terá movimento retilíneo e
uniforme (
).