Didáctica da Física I ( ) ( )

Didáctica da Física I
Ano lectivo 2006/07
Folha de exercícios nº1
Cinemática/Dinâmica
1. Num laboratório dois alunos mediram a posição dum carrinho que se movia sobre uma
mesa e obtiveram as seguintes coordenadas (S.I.) em relação a dois eixos ortogonais:
x(t ) = 5 2 + 4 2t − 2t 2
y (t ) = 5 2 + 4 2t − 2t 2 .
e
Determinar:
a) a equação da trajectória;
b) a expressão analítica da lei do movimento, sendo s o = 10 m;
c)
d)
e)
f)
o vector deslocamento no intervalo de tempo [0,3] s;
o deslocamento escalar no mesmo intervalo;
o espaço percorrido no mesmo intervalo;
Esboçar o gráfico da posição medida sobre a trajectória, da velocidade escalar e da
aceleração no intervalo [0,5] s.
g) Caracterizar o tipo de movimento do carrinho.
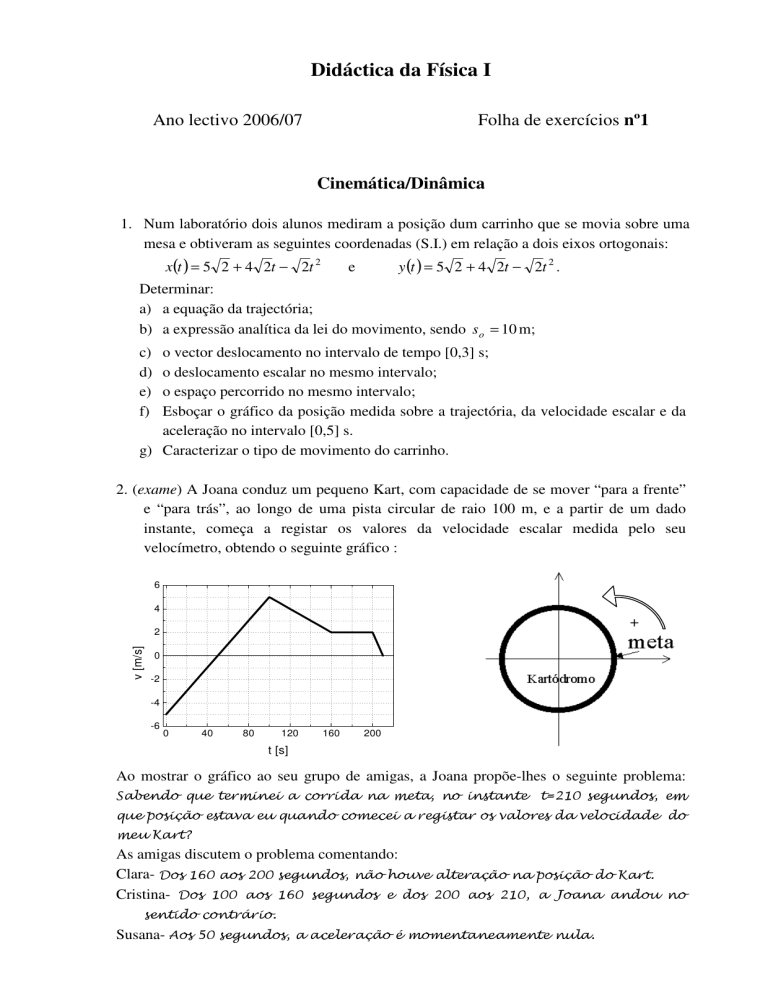
2. (exame) A Joana conduz um pequeno Kart, com capacidade de se mover “para a frente”
e “para trás”, ao longo de uma pista circular de raio 100 m, e a partir de um dado
instante, começa a registar os valores da velocidade escalar medida pelo seu
velocímetro, obtendo o seguinte gráfico :
6
4
+
v [m/s]
2
0
-2
-4
-6
0
40
80
120
160
200
t [s]
Ao mostrar o gráfico ao seu grupo de amigas, a Joana propõe-lhes o seguinte problema:
6DEHQGR TXH WHUPLQHL D FRUULGD QD PHWD QR LQVWDQWH W
VHJXQGRV HP
TXHSRVLomRHVWDYDHXTXDQGRFRPHFHLDUHJLVWDURVYDORUHVGDYHORFLGDGHGR
PHX.DUW"
As amigas discutem o problema comentando:
Clara- 'RVDRVVHJXQGRVQmRKRXYHDOWHUDomRQDSRVLomRGR.DUW
Cristina- 'RV DRV VHJXQGRV H GRV DRV D -RDQD DQGRX QR
VHQWLGRFRQWUiULR
Susana- $RVVHJXQGRVDDFHOHUDomRpPRPHQWDQHDPHQWHQXOD
2
Joaquina-
1R LQWHUYDOR > @ R HVSDoR SHUFRUULGR QmR FRLQFLGH FRP R
GHVORFDPHQWR
a) Faça um comentário breve às afirmações das amigas da Joana, dizendo
explicitamente se são verdadeiras ou falsas.
b) Calcule a aceleração do Kart no instante 180 s.
c) Calcule a posição inicial do movimento.
3. (exame) Considerar a seguinte situação de trânsito, ilustrada na figura. Um carro com
velocidade inicial de grandeza 36 km/h, inicia a
ultrapassagem do motociclo ao longo de uma curva
(R=200 m). O motociclo mantém a grandeza da sua
velocidade, 36 km/h, constante. Um autocarro, que
no início da ultrapassagem está a uma distância de
100 m do carro e com velocidade de 10,8 km/h,
começa a travar, diminuindo a grandeza da sua
velocidade de 1300 km/h em cada hora.
a) Se o carro iniciar a ultrapassagem 10 metros atrás do motociclo e terminá-la
regressando à sua faixa de rodagem, 10 metros à frente do motociclo, qual deve ser
a aceleração mínima do carro, suposta constante durante toda a ultrapassagem, para
que a ultrapassagem se faça sem acidentes?
b) Marcar no instante t=2s, o vector aceleração dos três veículos e justifique o seu
módulo, sentido e direcção. (Se não resolveu a alínea anterior faça aceleração_do_carro=1m/s2).
4. No decorrer duma aula sobre dinâmica e após terem sido enunciadas as leis de Newton,
um aluno coloca ao professor a seguinte questão:
“Uma vez que as forças que actuam num corpo são responsáveis pela alteração do seu
movimento, expressa através da lei fundamental da dinâmica, porque razão quando
termino o meu almoço e as paredes do meu estômago se comprimem durante a digestão
dos alimentos, estas forças não me provocam qualquer tipo de movimento?”
Admitindo que era o professor desse aluno, elabore uma resposta à questão apresentada
por forma a clarificar inequivocamente o seu aluno.
5. Após a explicação dada ao aluno do problema 4, um outro interroga o professor da
seguinte maneira:
“Quando ando de bicicleta, a força que exerço com os meus pés nos pedais da minha
bicicleta permitem que eu (juntamente com a bicicleta) me movimente. No entanto,
quando está muito frio e se forma gelo na estrada, apesar de exercer as mesmas forças
(ou mais...) nos pedais não consigo obter qualquer movimento. Será que as leis de
Newton não se aplicam neste caso?
Como responderia a esta questão de forma a esclarecer o seu aluno.
3
6. (Comboio do Texas, problema proposto) Considere uma linha de comboio
“perfeitamente horizontal” onde circula, com velocidade constante de 30 km/h, uma
carruagem de mercadoria aberta no topo. Subitamente, começa a chover de forma
torrencial e a carruagem vai ficando cheia de água. Finalmente, pára de chover e
constata-se que a carruagem fica com uma massa de água equivalente ao dobro da sua
massa (em vazio). Entretanto e passado algum tempo, abre-se um buraco na base da
carruagem que permite que a água vá escoando até a carruagem ficar novamente vazia.
Determinar a velocidade final da carruagem, nas seguintes
condições:
A chuva caiu na vertical relativamente ao solo;
A chuva caiu na vertical relativamente à carruagem.
7. (exame) Um passageiro viaja clandestinamente no vagão de mercadorias de um combóio.
No instante inicial o combóio parte do repouso e começa a acelerar com a = 3 m/s2, em
relação à estação. O passageiro vê então um caixote (massa = 1 Kg) na extremidade B
do combóio, dirigir-se a ele com a = 1 m/s2.
a) Do ponto de vista do passageiro, que forças actuam no caixote? Desenhe-as, faça a
respectiva legenda e calcule os seus módulos.
b) E do ponto de vista de um observador inercial na estação? Desenhe as forças e faça
a respectiva legenda.
c) Do ponto de vista do passageiro quanto tempo demora o caixote a atingi-lo?
d) E do ponto de vista do observador na estação, quanto tempo demora o caixote a
atingir o passageiro?
e) Suponha agora que está um gato em cima do caixote enquanto este se move em
direcção ao passageiro, para o gato que forças actuam no caixote? Desenhe-as e
faça a respectiva legenda.
a
5 metros
A
B
8. (exame) Num livro de exercícios de Física está o seguinte problema :
Uma pintora de paredes de 60 Kg está sobre uma plataforma de alumínio de 15 Kg.
Uma corda está amarrada à plataforma e passa por uma roldana, podendo a pintora
puxar a corda para subir.
Qual a força que a pintora deve exercer na corda para
subir com aceleração de 0.8 ms-2? Considere a
roldana ideal e a massa da corda desprezável.
Um aluno resolveu-o da seguinte forma:
4
$IRUoDGHWHQVmRTXHSX[DRHOHYDGRUpHPPyGXORLJXDOjIRUoD)TXHDSLQWRUDH[HUFH(VWDIRUoD
WHPTXHYHQFHURSHVRHRULJLQDUDDFHOHUDomRGHVHMDGD
) P
P
JP
P
D
[[ 1
SLQWRUD
HOHYDGRU
SLQWRUD
HOHYDGRU
Critique a resolução do aluno, dizendo explicitamente se esta está ou não correcta. Se
não concordar com o aluno, resolva o problema correctamente.
9. Considere uma roldana de massa desprezável e dois corpos A e B ligados entre si por um
fio como mostra a figura. O fio tem massa desprezável e é inextensível. Sobre a roldana
exerce-se uma força F de intensidade variável F = 4t2 j (SI). Considere a aceleração da
gravidade igual a 10 ms-2. A massa de B é 2 kg e a de A é 1 kg. No instante inicial todos
os corpos têm velocidade nula.
a) Desenhe as forças que actuam nos corpos (A,
y
F
B e roldana) e faça a respectiva legenda.
b) Calcule a aceleração do corpo A e a do corpo
B.
c) Qual o vector velocidade do corpo A ao fim
de 1 segundo?
d) A que distância do eixo dos xx está o centro
de massa do sistema (corpo A, corpo B,
A
B
roldana e fio) ao fim de 2 segundos ?
x
10. Considere um cubo e uma esfera que descem um plano inclinado (de inclinação α)
muito polido. Cubo e esfera, ambos homogéneos e de massa m, partem do repouso, e
percorrem a mesma distância l até atingirem a parte mais baixa do plano inclinado.
Utilizando as leis de Newton, calcule qual deles chega primeiro ao solo e com que
velocidade.
Repita o problema considerando o plano muito rugoso.
11. Faça a legenda e complete o gráfico
seguinte que diz respeito ao módulo da
velocidade do centro de massa e da
velocidade angular de uma esfera rígida e
homogénea de raio R=10 cm, que é
lançada horizontalmente com velocidade
inicial de 10 m/s, numa superfície
horizontal com coeficiente de atrito 0.1.
[I=2/5MR2]
80
10,0
9,5
60
9,0
40
8,5
8,0
20
7,5
0
7,0
0
2
4
t (em segundos)
6
8
5
12. (Bola de bilhar. A tacada) Considere uma bolha de bilhar (massa, m=200g, raio, R=5
cm e momento de inércia relativamente a um eixo que passa pelo centro de massa da bola,
I=2/5 mR2) sobre uma mesa de bilhar e na qual é aplicada uma tacada com ilustrado nas
figuras (caso 1 – “puxar” a bola e caso 2 – “avançar” a bola). Por acção dessa tacada a bola
adquire uma velocidade de centro de massa de 50 cm/s e uma velocidade angular de 40
rad/s com direcção perpendicular ao plano da folha e com o sentido representado.
Construa os gráficos da velocidade do centro de massa e da velocidade angular da bola em
função do tempo para os dois casos ilustrados.
Caso 1
Caso 2
&
ω§
&
ω
&
vCM ←
&
vCM ←
Coeficiente de atrito entre a bola e a superfície da mesa de bilhar: cinético, µC = 0.5
estático, µE = 0.9
13. (exame) Na figura os blocos A e B têm massa 1 e 5 Kg respectivamente. Entre A e B
existe atrito (µe = µc = 0.1) mas B pode-se deslocar sem atrito sobre a superfície
horizontal. No instante inicial A move-se com velocidade v0 = 1,2 i (m/s), enquanto B
está em repouso.
Um observador inercial diz que A diminuiu a sua velocidade enquanto B a aumentou,
até que ambos se deslocam com a mesma velocidade.
A
B
x
a) Acha possível a situação que o observador descreve? Como a explica?
b) Que distância percorre o bloco A até os blocos se moverem com a mesma
velocidade?
6
14. Num exame de Física constava o seguinte problema.
Uma rampa em forma de quarto de circunferência, e de massa M, é colocada numa mesa
horizontal sem atrito. Uma pequena bola de massa m coloca-se no topo da rampa e soltase, deixando-se deslizar ao longo da superfície polida da rampa. Qual a velocidade da
rampa no instante em que a bola deixa a rampa?
Um aluno resolveu-o da seguinte forma:
7DQWRDERODFRPRRVLVWHPDERODUDPSDSRUTXHQmRKiQHQKXPD
IRUoD GLVVLSDWLYD D UHDOL]DU WUDEDOKR FRQVHUYDP D VXD HQHUJLD
PHFkQLFD(QWmRSDUDRVLVWHPD
∆S ⇒0Y
[
∆(
P
0
PY P
⇒PJ5 PY 0Y
P
0 ⇒9 P J50 P
Critique a resolução do aluno.
0
15. (problema proposto) Uma barra NÃO HOMOGÉNEA, muito fina, está pousada em
cima de uma mesa polida. Não existe atrito entre a mesa e a barra. Lança-se um disco
com massa = 1 Kg e velocidade v = 5 m/s, contra a barra.
i) Da primeira vez o disco atinge a barra no ponto y=2 e
verifica-se que após o choque o disco fica parado e a barra
move-se em linha recta com v=1 m/s.
y
2
1
5
y
x
A
2
1
5
x
ii) Da segunda vez prende-se a barra numa das extremidades
(ponto A) à mesa. O disco atinge o centro da barra (y = 1,5 m)
e verifica-se que este fica incrustado na barra. A barra adquire
um movimento de rotação dando uma volta completa em cada
40 segundos.
a) Diga se para cada um dos choques :
- Há conservação da quantidade de movimento do sistema.
- Há conservação da energia mecânica do sistema.
- Há conservação do momento angular do sistema.
( justifique muito sucintamente)
b) Determine a massa da barra.
c) Determine o momento de inércia da barra em relação a A.
d) Determine a posição do centro de massa da barra.
7
16. (exame) Uma pistola “lança-setas” é constituída por uma
mola elástica, cuja constante elástica é K = 4000 N/m, e está
suspensa por um fio, de massa desprezável, como ilustra a
figura. A massa da pistola é 200 g e a massa da seta é 2 g.
Quando carregada com uma seta a energia potencial elástica
da mola é 0,2 J. A pequena distância da pistola encontra-se
uma placa quadrada de madeira que pode rodar, livremente,
em torno de um eixo que passa pelo seu centro (ponto O da
figura). A placa tem massa M = 200 g, lado L = 5 cm e
espessura 0,1 cm. O momento de inércia da placa relativamente a um
eixo que contém um dos lados da placa (quadrado) que passa em O’, é
I O ' = 13 ML2 .
a) Disparando a pistola automaticamente, qual é a velocidade da seta à saída da pistola?
b) Qual é a altura máxima alcançada pela pistola?
c) Desprezando o efeito da gravidade sobre a seta no seu percurso até à placa, e sabendo
que a mesma fica presa, junto à extremidade superior, na placa de madeira,
determinar o número de rotações da placa por segundo, após o impacto da seta.
(Ignore o acréscimo de massa relativo à seta quando presa na placa.)
d) Diga, justificando, qual a dependência do ponto de impacto da seta com a placa, no
valor do número de rotações da placa por segundo.
17. (exame) A Laura, à procura de apontamentos antigos de Física, foi ao sótão de sua casa,
mas ao descer, largou a porta tipo alçapão e esta atingiu-a na cabeça como mostra a
figura.
Considere que a porta pode rodar sem atrito em
torno de um eixo horizontal e com momento de
inércia ml2/3 ( m a massa da porta e l a sua
largura). Considere ainda que, quando a Laura
largou a porta, esta estava em repouso
praticamente na posição vertical.
a) Marque as forças que actuam na porta
quando esta está na posição que a figura
indica e legende-as.
b) Explicando o acontecido, a Laura diz:
Posso considerar que existe conservação do momento angular da porta durante a
queda pois, em relação ao centro de massa, todas as forças têm momento nulo.
Diga explicitamente se concorda ou não com a Laura, explicando o erro de
raciocínio se existir.
c) Qual o impulso que a Laura recebeu vindo da porta quando esta a atingiu na cabeça
considerando que depois do choque a porta ficou em repouso? (aceleração da
gravidade = g)
8
18.
(exame) Considerar os dois iô-iô’s apresentados na figura de igual massa M e raio
maior R. No primeiro caso (iô-iô tradicional) o fio enrola no pequeno cilindro interior de
raio R/2, enquanto que no segundo caso (iô-iô invertido) o fio enrola no cilindro exterior de
raio R.
Numa aula de Física, um aluno apresenta
dificuldades em interpretar o movimento
)
dos iô-iô’s quando estes são colocados na
horizontal, o 1º sobre uma superfície e o 2º
sobre uma calha dupla aberta, e lhe é
&
aplicada uma força F horizontal de
pequena intensidade de forma que não
exista deslizamento do iô-iô relativamente
)
à superfície onde apoia.
Sem recorrer a cálculo, explique de forma inequívoca qual o movimento de ambos os iôiô’s.
Caracterizar a aceleração do centro de massa dos iô-iô’s bem como a força de atrito em
ambos os casos.
n.b.: considerar o momento de inércia de ambos os iô-iô’s, relativamente ao seu eixo,
como sendo I o = 12 MR 2 , onde M representa a massa do iô-iô e R o raio maior; e o fio com
massa e espessura desprezáveis.
19. (exame) Um cilindro de massa m e raio R encontra-se
envolvido por muitas voltas de fio de massa e espessura
0
P
desprezáveis. A outra extremidade do fio encontra-se
5
ligado a um bloco de massa M, como é ilustrado na figura.
&
2
Aplica-se uma força F no centro de massa do cilindro.
O momento de inércia do cilindro relativamente a um eixo que passa no ponto O (ponto de
contacto do cilindro com a superfície) e é paralelo ao eixo do cilindro é I O = 32 mR 2 .
Determinar para as seguintes situações as acelerações do cilindro, angular e do centro de
massa, e do bloco:
a) ausência de atrito entre a superfície de apoio e os corpos (bloco e cilindro).
b) ausência de atrito entre a superfície e o bloco e presença de atrito entre a
superfície e o cilindro de tal forma que não haja deslizamento do cilindro.
20. (exame) Numa demonstração, durante uma aula,
foi utilizada uma miniatura dum carril de combóio
montado sobre uma grande roda que podia girar
livremente, com atrito desprezável, em torno dum
eixo vertical (ver figura). Um combóio de brincar,
com massa m, foi colocado sobre o carril e, com o
sistema inicialmente em repouso, foi ligada à
alimentação eléctrica. O combóio atinge uma velocidade escalar estacionária v
relativamente ao carril.
)
9
a) Traçar, justificando, os diagramas de forças no combóio (considere-o como um
ponto material) e no carril.
b) Qual a velocidade angular ω da roda se for M a sua massa e R o seu raio (despreze a
massa dos raios da roda e do carril, isto é considerar a massa M da roda como
estando distribuída uniformemente à distância R do seu centro).
c) Se for ∆t o intervalo de tempo necessário para o combóio atingir a velocidade
estacionária relativamente ao carril determinar o momento médio criado pelo motor
do combóio nas suas rodas motrizes.