matrizes, determinantes e sistemas – ufsc – 2003 a 2011

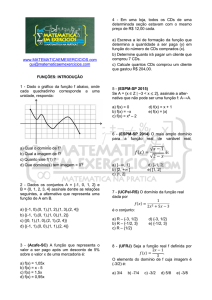
MATRIZES, DETERMINANTES E SISTEMAS – UFSC – 2003 A 2011
→ (UFSC 2003) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões)
CORRETA(S).
01. O número de elementos de uma matriz quadrada de ordem 12 é 48.
x x x
02. A soma das raízes da equação 4 x x = 0 é 8.
4
4 x
04. Uma matriz quadrada pode ter diversas matrizes inversas.
08. Somente podemos multiplicar matrizes de mesma ordem.
3x − 2y = 0
16. O sistema 
é indeterminado.
x + y = 0
Gabarito: 02
→ (UFSC 2004) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões)
CORRETA(S).
1
4
01. A matriz 5

3
2 3 0
2 5 1

não possui inversa.
4 8 1

1 2 0
02. Se um sistema de equações é indeterminado, então não se pode encontrar solução para ele.
04. Uma pequena indústria produz três tipos de produto que indicamos por x, y, z. As unidades
vendidas de cada produto e o faturamento bruto da empresa em três meses consecutivos são os
dados na tabela abaixo. Então, os preços dos produtos x, y e z só podem ser, respectivamente,
R$ 1.000,00, R$ 5.000,00 e R$ 3.000,00.
Unidades de x Unidades de y Unidades de z
Faturamento
Mês
vendidas
vendidas
vendidas
bruto
1
1
5
3
R$ 35.000,00
2
4
1
2
R$ 15.000,00
3
5
6
5
R$ 50.000,00
08. A solução da equação
2
4 1
2
4
3 1
Gabarito: 01+08 = 09
x = 0 é x = 1.
2
→ (UFSC 2005) Assinale a(s) proposição(ões) CORRETA(S).
 x + 2y = 9
01. O par ordenado (x, y) = (5, 2) é a única solução do sistema 
3x + 6y = 27
02. A matriz A = (aij)1×3, tal que aij = i –3j é A = [− 2 − 5 − 8 ] .
1 1
04. A soma dos elementos da inversa da matriz 
 é igual a 2.
0 1
08. Uma matriz quadrada A se diz anti-simétrica se tA =
0 0
Nessas condições pode-se afirmar que a matriz 0 0
1 0
-A, sendo tA a transposta da matriz A.
1
0  é anti-simétrica.
0 
16. Se as matrizes P, Q e R são escolhidas entre as listadas a seguir, para que PQ – R seja uma
matriz nula, o valor de x deve ser 2.
3 
1 , [3x 5],  6
0
 

2 
−1
2
1
x
 19 
, 6 
  
32. A e B são matrizes quadradas de ordem 2 tais que A = 5B. Nestas condições pode-se afirmar
que det(A) = 5det(B), sendo que det(A) e det(B) designam, respectivamente, os determinantes
das matrizes A e B.
Gabarito: 02+16 = 18
→ (UFSC 2006) Assinale a(s) proposição(ões) CORRETA(S).
01. Se K = (kij) é uma matriz quadrada de ordem 2 dada por kij = 22i + j para i < j e
kij = i2 + 1 para i ≥ j, então K é uma matriz inversível.
02. Chamamos “traço de L” e anotamos tr(L) a soma dos elementos da diagonal principal de uma
matriz quadrada L; então tr(L) = tr(Lt).
04. Sejam as matrizes M e P, respectivamente, de ordens 5 x 7 e 7 x 5. Se R = M.P, então a
matriz R2 tem 625 elementos.
08. Se A e B são matrizes tais que A.B é a matriz nula, então A é a matriz nula ou B é a matriz nula.
Gabarito: 01+02 = 03
→ (UFSC 2007) Pedro, Luiz, André e João possuem, juntos, 90 CDs. Se tirarmos a metade dos CDs
de Pedro, dobrarmos o número de CDs de Luiz, tirarmos 2 CDs de André e aumentarmos em 2 o
número de CDs de João, eles ficarão com a mesma quantidade de CDs. Determine o número inicial
de CDs de André.
Assinale o resultado encontrado no cartão-resposta.
Gabarito: 22
→ (UFSC 2008) A figura a seguir mostra os cartazes da loja de eletrodomésticos “PREÇO BOM”,
que está fazendo uma promoção de venda “casada” para vender dois eletrodomésticos. Com base
nos dados fornecidos pelos cartazes, determine o valor, em reais, da décima parte do preço do forno
de microondas.
PREÇO BOM – ELETRODOMÉSTICOS
Se comprar um Forno de Microondas e
um Refrigerador, você só pagará
R$ 1.490,00
Se comprar um Refrigerador e
um Fogão, você só pagará
R$ 1.750,00
Se comprar um Fogão e
um Forno de Microondas, você só pagará
R$ 840,00
Assinale o resultado encontrado no cartão-resposta.
Gabarito: 29
 0 x 1


→ (UFSC 2008) Considere as matrizes: A =  y − 1 0  , B =
1 z 0


y e z variam no conjunto dos números reais.
− 1 1 


 y 0 e C =
 1 x


7

− 6
2

2

3  , onde x,
z 
Assinale a(s) proposição(ões) CORRETA(S).
 64 
 
01. Para z = 0 existe uma matriz X, cuja soma dos elementos é 7, tal que C . X = - 69  .
 20 
 
02. A matriz A admite inversa se e somente se yz ≠ −1.
1
t
04. A matriz transposta de B é B = 
x
y − 1
.
0 1
08. Se A.B = C, então x + y + z = 5.
Gabarito: 01+02 = 03
→ (UFSC 2009) Assinale a(s) proposição(ões) CORRETA(S).
01. O elemento a64 da matriz A = (ai j) de ordem 8, onde ai j = (− 1)i + j ⋅
02. O triângulo ABC, cujas coordenadas dos vértices são
unidades de área.
2i
, é 3.
j
A(0,0), B(0,2) e C(10,20), tem 20
04. Para duas matrizes A e B de mesma ordem, vale sempre: (AB)t = At Bt.
 1
08. A matriz inversa da matriz A = 
− 5
 1
2
–1
é a matriz A = 

− 1
1
 5
1
2 .
1 

16. O elemento b23 da matriz B = At, onde A = (ai j)3x 2, e ai j = 2i + j, é 8.
Gabarito: 01+16 = 17
→ (UFSC 2011) Assinale a(s) proposição(ões) CORRETA(S).
 x + 3y − 2z = 0

01. As soluções do sistema homogêneo  x − 8y + 8z = 0
são ternas ordenadas do tipo ( a, b, c)
3x − 2y + 4z = 0

com ( a + b + c ) múltiplo de 11.
02. O valor de x para que os pontos A(3, –5), B(x,9) e C(0,2) sejam colineares é 3.
b 
a b
 a
 , então det B = 8 para B = 
 .
c d 
 2a + c 2b + d 
04. Se det A = 8 para A = 
08. Se A, B, C são matrizes inversíveis, então
[(AB
) .( AC )]
−1 −1
 2 5
 14 − 5 
 então ( A + A−1 − At ) 2 = 
 .
1 3 
 − 25 9 
16. Se A = 
Gabarito: 04+16 = 20
−1
. B = C.