Exame - Porto Editora

PROVA 615/14 Págs.
EXAME NACIONAL DO ENSINO SECUNDÁRIO
12.º Ano de Escolaridade
(Decreto-Lei n.º 286/89, de 29 de Agosto)
Programa novo implementado em 2005/2006
Duração da prova: 120 minutos
2.ª FASE
2007
PROVA ESCRITA DE FÍSICA
VERSÃO 2
Na sua folha de respostas, indique claramente a
versão da prova.
A ausência dessa indicação implica a anulação de
todos os itens de escolha múltipla.
V.S.F.F.
615.V2/1
Identifique claramente os grupos e os itens a que responde.
Utilize apenas caneta ou esferográfica de tinta azul ou preta.
É interdito o uso de «esferográfica-lápis» e de corrector.
As cotações da prova encontram-se na página 14.
A prova inclui, na página 3, uma Tabela de Constantes e, nas páginas 3,
4 e 5, um Formulário.
Pode utilizar máquina de calcular gráfica.
Nos itens de escolha múltipla
– SELECCIONE a alternativa CORRECTA.
– Indique, claramente, na sua folha de respostas, o NÚMERO do item
e a LETRA da alternativa pela qual optou.
– É atribuída a classificação de zero pontos às respostas em que
apresente:
• mais do que uma opção (ainda que nelas esteja incluída a opção
correcta);
• o número e/ou a letra ilegíveis.
– Em caso de engano, este deve ser riscado e corrigido, à frente, de
modo bem legível.
Nos itens em que seja solicitada a escrita de um texto, a classificação
das respostas contempla aspectos relativos aos conteúdos, à
organização lógico-temática e à terminologia científica.
Nos itens em que seja solicitado o cálculo de uma grandeza, deverá
apresentar todas as etapas de resolução.
Os dados imprescindíveis à resolução de alguns itens específicos são
indicados no final do seu enunciado, nos gráficos, nas figuras ou nas
tabelas que lhes estão anexadas ou, ainda, na Tabela de Constantes e
no Formulário.
615.V2/2
CONSTANTES
Velocidade de propagação da luz no vácuo
c = 3,00 × 108 m s–1
Módulo da aceleração gravítica de um corpo
junto à superfície da Terra
g = 10 m s–2
Massa da Terra
M T = 5,98 × 1024 kg
Constante da Gravitação Universal
G = 6,67 × 10–11 N m2 kg–2
Constante de Planck
h = 6,63 × 10–34 J s
Carga elementar
e = 1,60 × 10–19 C
Massa do electrão
me = 9,11 × 10–31 kg
Massa do protão
mp = 1,67 × 10–27 kg
1
K0 = —––
4π ε 0
K0 = 9,00 × 109 N m2 C–2
FORMULÁRIO
• 2.ª Lei de Newton......................................................................................
→
→
→
F = ma
F – resultante das forças que actuam num corpo de massa m
→
a – aceleração do centro de massa do corpo
• Módulo da força de atrito estático ........................................................
µe – coeficiente de atrito estático
N – módulo da força normal exercida sobre o corpo pela superfície
em contacto
Fa ≤ µe N
• Lei de Hooke .............................................................................................
F – valor da força elástica
k – constante elástica da mola
x – elongação
F = –k x
→
• Velocidade do centro de massa de um sistema de n partículas ............
mi – massa da partícula i
→
vi – velocidade da partícula i
• Momento linear total de um sistema de partículas ..............................
M – massa total do sistema
→
→
→
m1v1 + m2v2 + ... + mnvn
VCM = –——–————————
m1 + m2 + ... + mn
→
→
P = M VCM
→
VCM – velocidade do centro de massa
• Lei fundamental da dinâmica para um sistema de partículas .............
→
Fext – resultante das forças exteriores que actuam no sistema
→
Fext
→
dP
= –—
dt
→
P – momento linear total
• Lei fundamental da hidrostática .............................................................
p, p 0 – pressão em dois pontos no interior de um fluido em equilíbrio,
cuja diferença de alturas é h
p = p0 + ρ g h
ρ – massa volúmica do fluido
V.S.F.F.
615.V2/3
• Lei de Arquimedes..............................................................
I – impulsão
ρ – massa volúmica do fluido
V – volume de fluido deslocado
I = ρ Vg
1
1
2
2
• Equação de Bernoulli ........................................................ pA + ρ g hA + — ρ v A = pB + ρ g hB + — ρ v B
2
2
pA, pB – pressão em dois pontos, A e B, no interior de um
fluido, ao longo de uma mesma linha de corrente
hA, hB – alturas dos pontos A e B
vA, vB – módulos das velocidades do fluido nos pontos A e B
ρ – massa volúmica do fluido
• 3.ª Lei de Kepler..................................................................
R – raio da órbita circular de um planeta
T – período do movimento orbital desse planeta
• Lei de Newton da Gravitação Universal ...........................
→
Fg
R3
= constante
–—
T2
→
m1 m2 →
er
Fg = G –—–—
r2
– força exercida na massa pontual m2 pela massa
pontual m1
r – distância entre as duas massas
→
e r – vector unitário que aponta da massa m2 para a massa m1
G – constante da gravitação universal
• Lei de Coulomb...................................................................
→
Fe
– força exercida na carga eléctrica pontual q’ pela carga
eléctrica pontual q
r – distância entre as duas cargas colocadas no vácuo
→
e r – vector unitário que aponta da carga q para a carga q’
ε 0 – permitividade eléctrica do vácuo
• Lei de Joule ........................................................................
P – potência dissipada num condutor de resistência, R,
percorrido por uma corrente eléctrica de intensidade I
→
q q’ →
1
er
Fe = –—–— –—–—
4π ε 0
r2
P = R I2
• Diferença de potencial nos terminais de um gerador..... U = ε – r I
ε – força electromotriz do gerador
r – resistência interna do gerador
I – intensidade da corrente eléctrica fornecida pelo gerador
• Diferença de potencial nos terminais de um receptor....
ε ’ – força contra-electromotriz do receptor
r’ – resistência interna do receptor
I – intensidade da corrente eléctrica no receptor
U = ε ’ + r’ I
• Lei de Ohm generalizada ...................................................
ε – força electromotriz do gerador
ε ’ – força contra-electromotriz do receptor
R t – resistência total do circuito
ε – ε ’ = Rt I
• Associação de duas resistências
– em série ...........................................................................
Req = R1 + R2
– em paralelo .....................................................................
1
1
1
–— = –— + –—
Req R1
R2
Req – resistência equivalente à associação das resistências R1 e R2
615.V2/4
1
• Energia eléctrica armazenada num condensador .......... E = — C U 2
2
C – capacidade do condensador
U – diferença de potencial entre as placas do condensador
• Carga de um condensador num circuito R C

– condensador a carregar .................................................
Q (t ) = Cε  1 − e
– condensador a descarregar ...........................................
Q (t ) = Q0 e


−
−
t
RC




t
RC
R – resistência eléctrica do circuito
ε – força electromotriz do gerador
t – tempo
C – capacidade do condensador
• Acção simultânea de campos eléctricos e magnéticos
sobre cargas em movimento ............................................
→
Fem
→
→
→
→
F em = qE + qv × B
– força electromagnética que actua numa carga
→
eléctrica q que se desloca com velocidade
v num
→
ponto onde→existe um campo eléctrico E e um campo
magnético B
• Transformação de Galileu
x = x’ + vt
y = y’
z = z’
t = t’
Ö
• Relação entre massa e energia .........................................
∆E – variação da energia associada à variação da massa m
• Dilatação relativista do tempo ...........................................
∆t0 – intervalo de tempo próprio
∆E = ∆m c 2
∆t =
∆t 0
1–
v
2
c
2
v
2
c
2
• Contracção relativista do comprimento ..........................
L0 – comprimento próprio
L = L0 1 –
• Efeito fotoeléctrico .............................................................
f – frequência da radiação incidente
h – constante de Planck
W – energia mínima para arrancar um electrão do metal
Ecin – energia cinética máxima do electrão
hf = W + Ecin
• Lei do decaimento radioactivo .........................................
N(t) – número de partículas no instante t
N0 – número de partículas no instante t0
λ – constante de decaimento
N(t) = N0 e – λ t
• Equações do movimento com aceleração constante
1 →
→
→
→
r = r0 + v0 t + — a t2
2
→
→
→
v = v0 + a t
→
→
→
r – vector posição; v – velocidade; a – aceleração; t – tempo
V.S.F.F.
615.V2/5
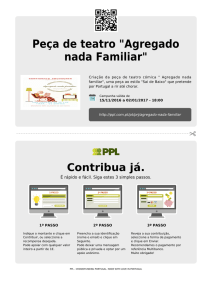
1. A figura 1 representa um bloco A, de massa mA, assente numa superfície horizontal e ligado, por
um fio inextensível e de massa desprezável, a uma esfera B, de massa mB. Os corpos encontram-se em movimento.
A
y
B
solo
x
Fig. 1
1.1. Tendo em conta a situação descrita, seleccione a alternativa correcta.
(A) O valor da aceleração dos corpos é inferior ao valor da aceleração da gravidade apenas
quando existe atrito entre o bloco A e a superfície horizontal.
(B) O valor da aceleração dos corpos é nulo quando a massa do bloco A é igual à massa da
esfera B.
(C) O movimento dos corpos é uniformemente retardado quando a massa do bloco A é maior
do que a massa da esfera B.
(D) O movimento dos corpos pode ser uniforme quando existe atrito entre o bloco A e a
superfície horizontal.
1.2. Admita que, numa dada experiência, há atrito entre o bloco A e a superfície horizontal.
Considere que os corpos adquirem uma aceleração de módulo 2,5 m s–2, sendo as massas
dos corpos A e B, respectivamente, iguais a 300 g e a 200 g.
Calcule o coeficiente de atrito cinético entre o bloco A e a superfície horizontal.
Apresente todas as etapas de resolução.
615.V2/6
1.3. Admita que a esfera B (de massa 200 g) se desprende do fio no instante em que a sua
velocidade tem módulo v. A partir desse instante, devido a uma rajada de vento, a esfera
→
passa também a estar sujeita à acção de uma força exterior F :
→
→
→
F = 3,00 e x + 2,00 e y (N).
Considere a origem do referencial ao nível do solo.
Seleccione o gráfico que melhor traduz a variação, ao longo do tempo, da coordenada de
posição y.
y
y
(B)
(A)
t
t
y
y
(C)
(D)
t
t
V.S.F.F.
615.V2/7
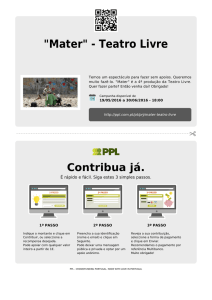
2. A figura 2 representa um corpo esférico, de massa 60,0 g, suspenso num fio de massa desprezável e
de comprimento , que é afastado da sua posição de equilíbrio, A, para a posição B. De seguida, o
corpo é libertado, passando a descrever um movimento oscilatório.
Considere o raio da esfera desprezável em relação ao comprimento do fio.
l
B
h=
A
1
l
4
Fig. 2
2.1. Trace o diagrama de forças aplicadas no corpo quando este se encontra na posição B e
determine o módulo da tensão do fio nessa posição.
Apresente todas as etapas de resolução.
2.2. Calcule o módulo da velocidade do corpo quando este passa na posição A, sabendo que o fio
tem um comprimento de 1,0 m.
Apresente todas as etapas de resolução.
2.3. Admita que o movimento oscilatório descrito pelo corpo é um movimento harmónico simples.
2.3.1. Tendo em conta a situação descrita, seleccione a alternativa correcta.
(A) O gráfico da raiz quadrada da frequência, f , em função do comprimento, , é uma
recta.
(B) O gráfico da frequência, f, em função da amplitude, A, é uma sinusóide.
(C) O gráfico do quadrado da frequência angular, ω 2, em função do comprimento, , é
uma hipérbole.
(D) O gráfico da frequência, f, em função da massa do corpo, m, é uma parábola.
2.3.2. Seleccione a alternativa que completa correctamente a seguinte afirmação.
A força restauradora numa posição entre A e B...
(A) ... é tanto menor, quanto maior for a massa do corpo.
(B) ... é tanto maior, quanto menor for a velocidade do corpo.
(C) ... é independente da posição do corpo.
(D) ... é independente do planeta onde o corpo oscila.
615.V2/8
3. A figura 3 representa um circuito constituído por um gerador ideal, um condensador plano, C, um
amperímetro, A, um reóstato, R, e dois interruptores, S1 e S2.
O condensador está inicialmente descarregado.
C
A
S1
R
S2
e
Fig. 3
3.1. Seleccione a alternativa que completa correctamente a seguinte afirmação.
Quando se fecha(m) o(s) interruptor(es)…
(A) ... S1, o condensador é carregado.
(B) ... S1 e S2, o amperímetro regista, momentaneamente, passagem de corrente.
(C) ... S1, há dissipação de energia no reóstato.
(D) ... S1 e S2, o amperímetro regista uma intensidade de corrente constante.
3.2. Com o condensador carregado, abre-se o interruptor S2, mantendo-se S1 fechado.
Justifique a seguinte afirmação:
Quanto menor for o valor da resistência introduzida pelo reóstato, R, menor é o tempo de
descarga do condensador.
3.3. Com o condensador carregado, abre-se o interruptor S1. Em seguida, afastam-se as placas do
condensador, aumentando para o dobro a distância entre elas.
Seleccione a alternativa que completa correctamente a seguinte afirmação.
A energia acumulada no condensador…
(A) ... reduz-se a metade.
(B) ... quadruplica.
(C) ... duplica.
(D) ... reduz-se a um quarto.
V.S.F.F.
615.V2/9
4. A figura 4 representa a Terra, T, um corpo A, em órbita em torno da Terra, e um corpo B, que foi largado
de um helicóptero em movimento a uma altitude constante relativamente à Terra.
A figura não está desenhada à escala.
A
B
T
Fig. 4
4.1. Tendo em conta a situação descrita, seleccione a alternativa correcta.
(A) A trajectória do corpo B, em relação a um referencial ligado ao helicóptero, é parabólica.
(B) A força que actua no corpo A tem uma componente centrípeta e outra componente
tangente à sua trajectória.
(C) A força que actua sobre o corpo B e a força que mantém o corpo A em órbita são da
mesma natureza.
(D) A trajectória do corpo B, em relação a um referencial ligado à Terra, é rectilínea.
1
4.2. Admita que as distâncias dos corpos A e B ao centro da Terra são, respectivamente, r e — r
3
e que os campos gravíticos, nas posições ocupadas pelos corpos A e B, são, respectivamente,
→
GA
→
e G B.
Seleccione a alternativa que completa correctamente a seguinte afirmação.
→
→
O quociente dos módulos de G A e G B é igual a…
(A) ... 3
(B) ... 9
1
(C) ... —
3
1
(D) ... —
9
615.V2/10
4.3. Considere a massa da Terra, MT, o módulo da velocidade do corpo A, v, a constante de
gravitação universal, G, e o raio da órbita descrita pelo corpo A, r.
4.3.1. Seleccione a alternativa que permite calcular o raio da órbita descrita pelo corpo A.
GMT
(A) r = ––––
v2
v2
(B) r = G –—
MT
v2
(C) r = –—–
GMT
GM
(D) r = ––––T
v
4.3.2. Demonstre que o trabalho realizado pela força gravítica, quando o corpo B, de massa
m, é transportado da altitude a que se encontra para a órbita do corpo A, é dado pela
expressão:
MTm
W B→ A = – 2 G –—–
r
5. Em 1900, Planck conseguiu explicar a radiação do corpo negro, admitindo que a absorção e a
emissão de radiação se faziam por pacotes de energia, os quanta.
Einstein, baseando-se nesta teoria, propôs que a própria luz fosse constituída por quanta,
posteriormente designados por fotões, conseguindo assim explicar o efeito fotoeléctrico. Einstein
revolucionou os conceitos sobre a natureza da luz, admitindo a sua dualidade.
5.1. Seleccione a alternativa correcta.
(A) O efeito fotoeléctrico consiste na colisão de um fotão com um electrão livre.
(B) No efeito fotoeléctrico, ocorre a ejecção de electrões de átomos por absorção de fotões.
(C) No efeito fotoeléctrico, aumentando a intensidade da luz incidente, aumenta a energia
cinética dos electrões ejectados.
(D) O efeito fotoeléctrico ocorre utilizando qualquer tipo de radiação.
5.2. Seleccione a alternativa que completa correctamente a seguinte afirmação.
Admitir a natureza corpuscular da luz permitiu explicar…
(A) … a interferência e a difracção da luz.
(B) … o efeito Compton e o efeito fotoeléctrico.
(C) … a difracção da luz e o efeito fotoeléctrico.
(D) … a interferência da luz e o efeito Compton.
V.S.F.F.
615.V2/11
5.3. Um feixe de radiação ultravioleta incide numa placa de sódio e remove electrões com uma
energia cinética máxima de 3,00 × 10–19 J/e.
5.3.1. Admita que se aplica um campo eléctrico uniforme, paralelo à direcção do movimento
dos electrões.
Calcule a intensidade do campo que anula, ao fim de 2,0 s, a velocidade dos electrões
que são ejectados com o valor máximo de energia cinética.
Apresente todas as etapas de resolução.
5.3.2. Justifique a seguinte afirmação:
Se sobre a placa de sódio incidir uma radiação de frequência superior à da radiação
ultravioleta, a energia cinética máxima dos electrões ejectados é superior a 3,00 × 10–19 J/e.
6. A figura 5 representa uma calha sobre a qual se colocaram os carrinhos A e B, de massas
respectivamente iguais a 120 g e 80 g. Na figura, estão também representadas duas células
fotoeléctricas, X1 e X2.
A
X1
B
y
X2
x
Fig. 5
Com este equipamento foram realizados três ensaios nos quais o carrinho A, inicialmente em
movimento, colidiu com o carrinho B, inicialmente em repouso, seguindo depois colados um ao
outro.
Na tabela, encontram-se registados os módulos das velocidades, vi e vf , obtidos experimentalmente, sendo vi a velocidade inicial do carrinho A, e sendo vf a velocidade final do conjunto
constituído pelos carrinhos A e B.
Tabela
615.V2/12
Ensaio
vi /m s–1
vf /m s–1
1
2
3
0,36
0,26
0,45
0,16
0,12
0,20
Calculando, para os ensaios realizados, o momento linear do sistema formado pelos dois carrinhos,
antes e depois da colisão, obteve-se o gráfico representado na figura 6.
pf / kg m s–1
0,06
0,04
0,02
0
0,02
0,04
0,06
pi / kg m s–1
Fig. 6
6.1. Determine o momento linear do sistema formado pelos dois carrinhos, antes e depois da
colisão, no ensaio 1.
Apresente todas as etapas de resolução.
6.2. Caracterize o impulso da força que o carrinho B exerce sobre o carrinho A, no ensaio 1.
6.3. Escreva um pequeno texto no qual refira se, nesta experiência, as leis de conservação
associadas às colisões se verificam, tendo em conta:
– o momento linear;
– as forças aplicadas;
– a energia cinética;
– o coeficiente de restituição.
FIM
V.S.F.F.
615.V2/13
COTAÇÕES
1.
1.1. .......................................................................................................................................
8 pontos
1.2. .......................................................................................................................................
14 pontos
1.3. .......................................................................................................................................
8 pontos
2.1. .......................................................................................................................................
10 pontos
2.2. .......................................................................................................................................
10 pontos
2.
2.3.
2.3.1. ............................................................................................................................
2.3.2. ............................................................................................................................
8 pontos
8 pontos
3.1. .......................................................................................................................................
8 pontos
3.2. .......................................................................................................................................
10 pontos
3.3. .......................................................................................................................................
8 pontos
4.1. .......................................................................................................................................
8 pontos
4.2. .......................................................................................................................................
8 pontos
3.
4.
4.3.
4.3.1. ............................................................................................................................
4.3.2. ............................................................................................................................
8 pontos
10 pontos
5.1. .......................................................................................................................................
8 pontos
5.2. .......................................................................................................................................
8 pontos
5.
5.3.
5.3.1. ............................................................................................................................
5.3.2. ............................................................................................................................
14 pontos
10 pontos
6.1. .......................................................................................................................................
10 pontos
6.2. .......................................................................................................................................
10 pontos
6.3. .......................................................................................................................................
14 pontos
___________
6.
TOTAL ....................................................... 200 pontos
615.V2/14