A que se deve o magnetismo

Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 1
A Lei da Indução de Faraday – Lei de
Lenz
B
v
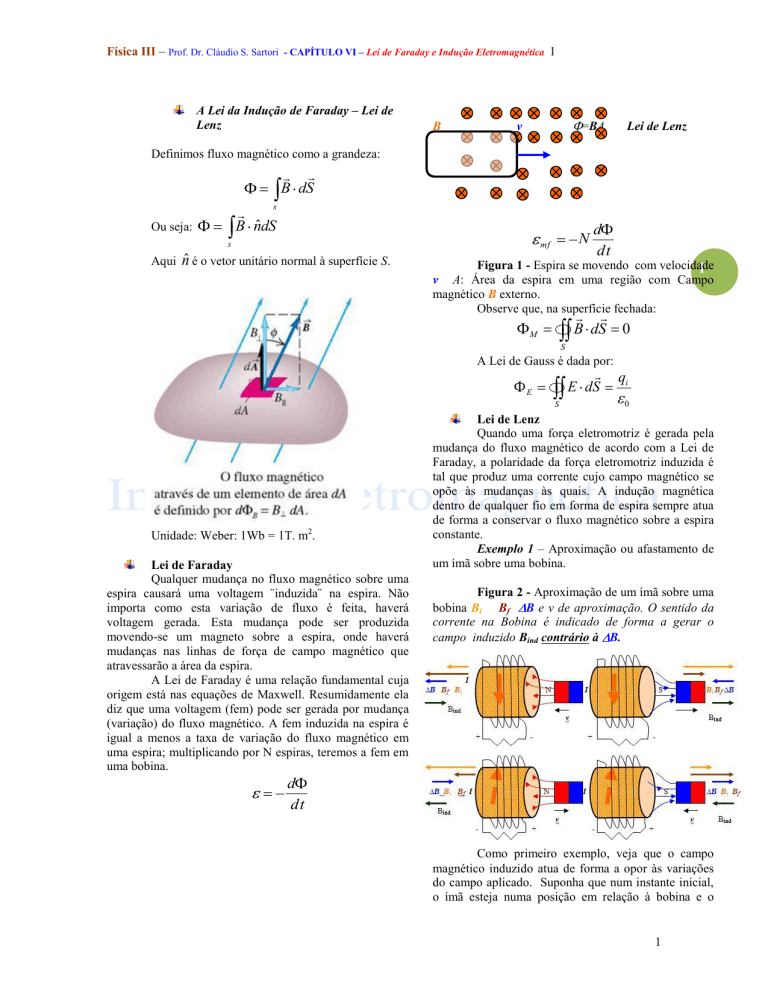
=BA
Lei de Lenz
Definimos fluxo magnético como a grandeza:
 
B dS
s

B nˆdS
Ou seja:
s
Aqui
N
mf
n̂ é o vetor unitário normal à superfície S.
d
dt
Figura 1 - Espira se movendo com velocidade
1
v A: Área da espira em uma região com Campo
magnético B externo.
Observe que, na superfície fechada:
M
 
B
 dS
0
S
A Lei de Gauss é dada por:
E

E
dS

S
Unidade: Weber: 1Wb = 1T. m2.
Lei de Faraday
Qualquer mudança no fluxo magnético sobre uma
espira causará uma voltagem ¨induzida¨ na espira. Não
importa como esta variação de fluxo é feita, haverá
voltagem gerada. Esta mudança pode ser produzida
movendo-se um magneto sobre a espira, onde haverá
mudanças nas linhas de força de campo magnético que
atravessarão a área da espira.
A Lei de Faraday é uma relação fundamental cuja
origem está nas equações de Maxwell. Resumidamente ela
diz que uma voltagem (fem) pode ser gerada por mudança
(variação) do fluxo magnético. A fem induzida na espira é
igual a menos a taxa de variação do fluxo magnético em
uma espira; multiplicando por N espiras, teremos a fem em
uma bobina.
qi
0
Lei de Lenz
Quando uma força eletromotriz é gerada pela
mudança do fluxo magnético de acordo com a Lei de
Faraday, a polaridade da força eletromotriz induzida é
tal que produz uma corrente cujo campo magnético se
opõe às mudanças às quais. A indução magnética
dentro de qualquer fio em forma de espira sempre atua
de forma a conservar o fluxo magnético sobre a espira
constante.
Exemplo 1 – Aproximação ou afastamento de
um ímã sobre uma bobina.
Figura 2 - Aproximação de um ímã sobre uma
bobina Bi Bf B e v de aproximação. O sentido da
corrente na Bobina é indicado de forma a gerar o
campo induzido Bind contrário à B.
d
dt
Como primeiro exemplo, veja que o campo
magnético induzido atua de forma a opor às variações
do campo aplicado. Suponha que num instante inicial,
o ímã esteja numa posição em relação à bobina e o
1
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 2
campo gerado pelo ímã seja

B i . Nesse momento, há linhas
de campo atravessando a área da seção transversal da
bobina, gerando assim um fluxo inicial. Ao afastarmos o

ímã com uma velocidade v ou aproximarmos, essas linhas
de campo também se afastarão ou aproximarão. Assim, o
campo magnético final externo sobre a bobina gerado pelo
ímã será

Bf
. Assim o aumento ou a diminuição do fluxo
segue à mesma variação do campo magnético:

B A

Bf

Bi A
2
Para sabermos o campo induzido sobre a bobina

Bin d , precisamos lembrar que, pela Lei de Lenz, ele se
opõe à variação do campo externo aplicado. Assim
precisamos sempre encontrar o sentido do vetor:

B

Bf

Bi
Para depois encontrarmos o sentido da corrente
elétrica induzida na expira para dar origem ao campo
magnético induzido

Bin d contrário à variação de

B.A
figura abaixo representa esse esquema, dependendo se

aproximamos o ímã com velocidade v .
Figura 3 – Aproximação de um ímã num circuito.
2
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 3
3
3
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 4
BA Blx
Exemplo 2 – Aproximação ou afastamento de uma
espira numa região de campo magnético uniforme.
Outro exemplo interessante é quando temos uma
espira se deslocando numa região onde há um campo
magnético uniforme. Observamos que, durante a passagem
da espira o fluxo varia, pois a área da espira sobre a região
de campo magnético uniforme varia (A). Sendo v a
velocidade da espira.
v
dx
dt
A
d BLx
dt
BL
d
dt
dx
dt
Bl
dx
dt
Blv
A direção da corrente deve antihorário, pois, de acordo com a Lei de Lenz, provoca um
campo contrário ao aumento de fluxo magnético sobre
o circuito elétrico.
A força sobre a Barra é dada por:

F
L x

F
d BA
dt
d
dt
A força eletromotriz induzida no circuito é
dada por:
 
qv B
Ilˆj B( kˆ)
 
Idl B
BIlˆj kˆ
4
BIliˆ
Ou seja, a força sobre a barra está para a
esquerda, contrária a velocidade.
B L v
Exemplo 4 – Campo e corrente induzida sobre
uma espira. Aplicação da regra da mão direita para o
caso em que o campo externo sobre a espira aumenta
ou diminui. Aplicação: guitarra elétrica.
Regra da mão direita para relacionar a corrente
induzida i com o campo magnético Bi que é produzido
quando o campo magnético externo B através da espira
aumenta (a,c) ou diminui (b,d)
Figura 5 – Fluxo sobre espira.
Figura 4 – Espira em movimento numa região de
campo magnético uniforme.
Exemplo 3 – Movimento de uma barra condutora
sobre trilhos em uma região de campo magnético uniforme.
A figura a seguir mostra uma barra condutora que
escorrega sobre dois trilhos condutores ligados a um
resistor. Um campo magnético uniforme está distribuído na
direção –k . Observe que o fluxo magnético através do
circuito está variando, pois a barra se move com velocidade
v.
O fluxo magnético em um dado instante é dado
por:
4
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 5
Esquema de uma bobina aplicada para o uso de
uma guitarra elétrica Quando ao corda da guitarra oscila,
há variação do fluxo sobre sobre a área de seção reta da
bobina, induzindo uma corrente.
Definimos fluxo magnético como a grandeza:
 
B dS
s

B nˆdS
Ou seja:
s
Aqui
n̂ é o vetor unitário normal à superfície
S.
v
dx
dt
A
d
dt
d BLx
dt
L x
5
d BA
dt
dx
BL
BLv
dt
A figura a seguir mostra uma barra condutora
que escorrega sobre dois trilhos condutores ligados a
um resistor. Um campo magnético uniforme está
distribuído na direção –k . Observe que o fluxo
magnético através do circuito está variando, pois a
barra se move com velocidade v.
Figura 8 – Fluxo
Figura 6
Exemplo 5 – Esquema indicando como varia as
linhas de campo ao mover a espira sobre uma região de
campo magnético uniforme. Observar o sentido da corrente
elétrica induzida na espira.
Figura 7 – Fluxo sobre espira.
5
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 6
O fluxo magnético em um dado instante é dado
por:
BA Blx
Figura 9 – Se a corrente está aumentando,
então uma voltagem em oposição é criada pelo campo
magnético da bobina.
A força eletromotriz induzida no circuito é dada
por:
d
dt
Bl
dx
dt
Blv
A direção da corrente deve anti-horário,
pois, de acordo com a Lei de Lenz, provoca um campo
contrário ao aumento de fluxo magnético sobre o circuito
elétrico.
A força sobre a Barra é dada por:

F
 
 
qv B Idl B
Ilˆj B( kˆ)
BIlˆj kˆ
6

F
BIliˆ
Ou seja, a força sobre a barra está para a esquerda,
contrária a velocidade
Indução Eletromagnética

Indutor
A indutância é a característica do comportamento
de uma bobina em resistir a qualquer mudança de corrente
elétrica sobre a espira. Da Lei de Faraday, teremos:
d
dt
d
dt
0
N
IA
l
0
N dI
A
l
dt
L
dI
dt
ou seja, a indutância L pode ser definida em
termos da fem ( ) gerada para se opor à mudança da
corrente elétrica.
d
dt
L
dI
dt
Verificamos que a indutância L depende das
características Geométricas do circuito. Se tivermos um
solenóide, o fluxo será dado por:
BNA
0 nINA
0
L
I
n2lAI
0
n2 Al
N
lAI
l
L I
2 A
0N
l
0n
Exemplo 6 – Calcular a auto-indutância de um
solenóide de 10 cm de comprimento, 5 cm2 de área e
100 espiras.
n
N
L
100
103
0,1
L
L 4 10 7 103
A
l
5 10 5
0
2
N2
2 10 5 H
 Unidade: Henry (H) 1H = 1 V.s/A
(1Henry=1 Volt.1Segundo/1 Ampére).
6
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 7
Figura 10 – Variações i na corrente chegando no
I (t )
indutor:
V
[1 e ( R / L)t ]
R
Observe que quando t aumenta sem limite, I
tende para V/R, que é a corrente prevista pela lei de
Ohm quando não há indutância presente.
Figura 11 – Circuito RL.
7
(a) Se a corrente i está aumentando, a força
eletromotriz induzida l aparece ao longo da bobina numa
direção que se opõe ao aumento.
(b) Se a corrente i está diminuindo, a fem induzida
aparece na direção que se opõe ao crescimento.

Circuito RL
A auto-indutância num circuito impede a corrente
de aumentar ou diminuir instantaneamente. Os circuitos que
contém bobinas ou solenóides com muitas espiras têm uma
grande auto-indutância. Esta bobina ou solenóide é um
indutor. O símbolo de um indutor é
Pode-se muitas vezes desprezar a auto-indutância
do restante do circuito em comparação com a indutância do
indutor. Nos circuitos que possuem batertias, resistores e
indutores chamamos de circuitos RL.
Um circuito RL simples consiste em um resistor R
e um indutor L ligados em série, conforme ilustrado na
figura ao lado, com uma força eletromotriz constante V.
Fechado o interruptor em t=0s, segue-se e uma das leis de
Kirchhoff para circuitos elétricos que,se t>0, a corrente I
satisfaz a equação diferencial:
Vc –Vc =Vc-Vb + Va – Vc + Vb-Va =
V
Figura 12 – Gráfico da corrente em função do
tempo.
dI
RI 0
dt
dI
L
RI V .
dt
L
Expresse I em função de t.

Circuito RL simples.
Podemos escrever a equação como:
dI R
V
( R / L)dt
I
e
e( R / L)t
dt L
L
Multiplicando-se a equação pelo FI
Dt ( Ie( R/ L)t )
( R / L)t
I e
V
L
V ( R / L )t
e
L
e
( R/ L)t
dt
Circuito RL, Chave S1 aberta e S2 fechada,
após a corrente no indutor atingir o máximo valor.
7
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 8
No circuito RL simples da figura anterior, as
chaves S1 e S2 são colocadas de modo que a bateria seja
removida do circuito. Depois da corrente no indutor ter
atingido seu máximo valor, com a chave S1 fechada, a
chave S2 é fechada e a S1 aberta. A corrente diminuirá com
o tempo conforme mostra a figura a seguir.
Nesse caso a soma das tensões é igual a zero:
dI
dt
I
dI
I
I0
L
I
ln
I0
RI
0
t
R
dt
L
0
I (t ) I0e
tc
R
t
L
L
, aqui é a chamada constante de tempo;
R
I (t ) I 0 e

8
R
t
L
t
tC
Indutância Mútua
O Fluxo através de um circuito pode ser
relacionado à corrente no circuito e às correntes em oputros
circuitos vizinhos, caso não existam ímãs nas vizinhanças.
Considere os esquemas dos circuitos a seguir:
Figura 13 – (a) Se a corrente na bobina (1) i1
muda, aparecerá uma fem induzida na bobina (2).
(b) Se a corrente na bobina (2) i2 muda, aparecerá
uma fem induzida na bobina (1).
O Campo magnético em um ponto P constituise da soma vetorial de dois campos, criados pela
passagem da corrente i1 no circuito 1 e pela passagem
da corrente i2 no circuito 2. Como esses campos são
proporcionais às correntes, podendo ser calculados pela
Lei de Biot-Savart, pode-se, portanto, encontrar o fluxo
através do circuito 2 pela equação:
L2 I 2
m2
M12I1
Aqui, L2 e M12 são constantes. A constante L2 é
denominada a auto-indutância do circuito 2, depende da
disposição geométrica deste circuito. A constante M12,
a indutância mútua dos dois circuitos, depende da
configuração geométrica de ambos. Quando os
circuitos estiverem muito afastados, a indutância mútua
será pequena, pois o fluxo no circuito 2 devido à
corrente i1 será menor.
Podemos escrever para o fluxo no circuito 1:
L1I1 M 21I 2
m1
Podemos mostrar que:
M12
M 21
Quando os circuitos estão fixos e apenas as
correntes variam, as forças eletromotrizes induzidas
são, pela lei de Faraday:
d
1
m1
dt
L1
dI 1
dt
M
dI 2
dt
Analogamente, no circuito 2, a fem será dada
por:
d
2
m2
dt
L1
dI 2
dt
M
dI 1
dt
8
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 9
Dessas equações vemos que o Henry, unidade do
SI de indutância, é dada por:
1T .m2
A
1H
1 VsA
Observe que quando há um só circuito, a fem
induzida pela lei de Faraday é:
L
dI
dt
Exemplo 6 – Calcular a taxa de variação na
corrente para um solenóide de 10 cm de comprimento, 5
cm2 de área e 100 espiras quando a fem induzida for de
20V.
Exemplo 7 – Projetar uma bobina de raio R e
número de voltas N para um circuito RL de resistência
1K de forma que a constante de tempo seja de 10 s.
L
L R tc
L
R
R 2 , teremos:
Como: A
2 A
R t c 10 3 10 L
0N
l
tc
10 4
0
R2
l
2
0N
10 7 N 2
4
A
l
N2
R2
l
9
2
L
dI
dt
dI
dt
20
2 .10 5
L
3,18.105
10 4
A
s
x
c
a
L
Se montarmos uma bobina com
comprimento de l = 3 cm e raio 2 cm teremos:
2,533 10 9 l
R
Para calcular o fluxo através da espira retangular,
devemos efetuar uma integração, onde o elemento de área é
dA = cdx
d
m
B dA
I
cdx
2 x
b
b
0I
d m
cdx
2
x
a
a
0
m
b
Ic 1
dx
2 ax
0
m
M
m
I
2,533 10 9 3 10
2,5.10 2
2
LI
dI
dt
RI 2
0
O termo associado ao armazenamento de
energia no Indutor é:
b
m
um
Energia Magnética
Quando instala-se uma corrente no circuito da
figura acima, apenas parte da energia fornecida pela
bateria é dissipada no resistor, o restante da energia é
armazenada no indutor. Observar que
EI
d
7
2,533 109 l
R
N
N
I
R
l
R2
N2
l
10 7 N 2
104
4 2 10
Um exemplo para o cálculo de indutância mútua:
Exemplo 6 – Calcular a indutância mútua entre um
fio comprido e uma espira retangular:
A figura aparece dois circuitos para os quais se
pode calcular a indutância mútua.
2
4
0
m
0
2
c
2
ln
b
a
Ic
ln
b
a
dU m
dt
LI
dI
dt
Um
Um
dU m
LI
2
f
LI dI
LI 2f
2
2
B lA
2 0
2
(Energia magnética armazenada num indutor)
Quando a corrente elétrica diminui, diminui a
energia no indutor e o campo magnético também
diminui.
Analogamente, o mesmo acontece quando
temos um capacitor carregado, para o caso do campo
Elétrico E. A energia eletrostática armazenada num
capacitor de placas paralelas.
Ue
QV
2
0
E 2 Ad
2
(Energia eletrostática armazenada num capacitor)
9
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 10
Em geral, numa região do espaço onde há campo
elétrico e magnético, definimos densidade de energia à
relação:
U
V
1
2
0
E
B2
2 0
2
I (t) Imax sen(
t)
Figura 15 – Circuito LC.
(a) Gráficos de carga versus tempo e corrente
versus tempo.
Circuito LC:
Suponha um capacitor inicialmente carregado com
uma carga Q0 e em t = 0 fechamos a chave do circuito
abaixo:
Figura 14 – Circuito LC.
10
(b) Transferência de energia magnética e
elétrica pelo indutor e capacitor.
Depois da chave fechada, a corrente é oposta e a
carga nas placas do capacitor e a corrente estão
relacionadas por
I
dQ
. No capacitor, de c para d, há
dt
uma queda de potencial Q/C e de a para b no indutor LdI/dt.
A regra de Kirchhoff aplicada ao circuito dá:
L
dI
dt
Q
C
0
ou
d 2Q
dt 2
1
Q
LC
0
A solução desta equação diferencial é dada por:
Q(t )
A cos( t
)
Onde:
1
é a frequência num circuito LC
LC
Vamos supor
Então teremos:
= 0 para a fase desse circuito.
Q(t) Qmax cos( t)
I (t)
Q0 sen( t)
10
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 11
Exemplo 8 – Num circuito LC, o valor da
indutância é L =2mH e da Capacitância C = 47 F. A carga
inicial do Capacitor vale Q0. Determine a frequência e os
gráficos Q(t) e I(t).
1
LC
1
2 10 47 10
3, 2613 103 rads
3
6
Figura 16 – Circuito LC.
(a) Gráficos da energia armazenada no capacitor
(UC) versus tempo e a energia armazenada no indutor (UL)
versus tempo.
11
Observe que a corrente oscila com a mesma
frequência da carga e está 900 fora de fase com a carga.
As Amplitudes são diferentes, como indicam nos eixos.
Veja que se fizermos um balanço das energias
magnética no indutor e eletrostática no capacitor,
teremos:
UT
(b) Analogia mecânica.
UE UL
)
2
Q2
2C
L
LI 2
2
Q0 sen( t
2
UT
Q0 cos( t
2C
UT
1
1
2
LC
LC
2 2
LQ
1 2
Q0 cos2 ( t
) 0 sen 2 ( t
2C
2
1 2
UT
Q0
2C
)
Substituindo
Ou seja, a energia total é constante no tempo.
11
)
2
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 12
Figura 18 – Circuito RLC – gráfico (t,Q ).
Circuito RLC:
(a) Caso:
No circuito RLC teremos um resistor em série a
um capacitor e a um indutor. Para a regra de Kirchhoff
incluimos a queda de potencial RI no resistor:
R
4L C
Figura 17 – Circuito RLC.
12
(b) Caso:
R
4L C
Observe a queda brusca da carga em pouco tempo.
L
dI
dt
Q
C
RI
(c) Analogia mecânica.
0
Derivando a equação com respeito a t teremos:
d 2I
d 2t
R dI
L dt
1
I 0
LC
Ou seja, se chamarmos de:
1
LC
0
d 2I
d 2t
R dI
L dt
2
0
I
0
A solução proposta é do tipo:
I H (t )
Aei
n
t
Be
i
n
t
e
R
2L
t
Aqui IH(t) a solução da equação diferencial
homogênea, com:
1 R 2 com
LC 4L2
n
2
0
n
f
Caso
0>
f2
R
2L
f a solução é dada por:
Tipos de soluções da equação diferencial para
a carga:
I H (t )
c1 cos
n
t
c2 sen
n
t e
R
2L
t
(a)
1
LC
R2
1
(b)
2
4L
LC
R2
1
(c)
2
4L
LC
R2
4 L2
12
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 13
Tensão Alternada
 Introdução
Mais de 99% da energia elétrica produzida no mundo é
obtida por geradores elétricos oeprando com corrente
alternada (AC). A vantagem sobre a corrente contínua é que
pode ser transportada a longas distâncias, a baixo valores de
corrente e altos de tensão, para ser reduzida a perda de
energia por efeito Joule; podendo assim, ser transformada
com o transformador, o qual utiliza o princípio da indução
magnética.
 Gerador de corrente alternada:
Um gerador simples de corrente alternada é uma
bobina girando em um campo magnético uniforme, como
ilustramos na figura abaixo:
Figura 19 – Gerador e esquema de hidrelétrica.
O princípio básico para um gerador de
corrente alternada é uma espira condutora girando em
um campo magnético uniforme. Na prática, a força
eletromotriz alternada induzida na espira de muitas
voltas de um fio é feita pelo contato entre o anel
conectado com a espira rotativa, cada um conectado
eletricamente por uma escova metálica ao resto do
circuito elétrico.
O vetor unitário normal n ao plano da bobina
faz um ângulo com o campo magnético uniforme B.
m
N B A cos
Aqui, N é o número de espiras, e A a área da13
bobina. Seja a velocidade angular da bobina, que é
mecanicamente acionada. Então:
t.
m
N B A cos t
A força eletromotriz induzida será dada por:
m
d m
dt
NBAcos t
NBA sen t
Ou
m
m
sen t
NBA
Pode-se gerar uma tensão senoidal numa
bobina fazendo-a girar com a velocidade angular
constante num campo magnético. Num diagrama de
um circuito, um gerador de corrente alternada (ca)
simboliza-se pelo símbolo:
A seguir discutiremos os circuitos de tensão
alternada simples e o circuito RLC.
13
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 14
Circuitos de tensão alternada.
Em eletrônica,
representam-se
fenômenos
ondulatórios por funções oscilantes como a seno e o
cosseno. Exemplificando na teoria de corrente alternada,
temos uma tensão variando da forma senoidal, assim, para
cada caso, a corrente e a tensão serão estudadas quando
submetemos essa tensão à um:

Corrente alternada com um Resistor:
Figura 20 – Circuito AC com resistor. (a)
Gráficos de tensão e corrente versus tempo ediagrama de
fasores (b).
14
Figura 21 – Circuito AC . Corrente (a) e corrente
média em função do tempo (b).

Equações:
Equações (Lei de Ohm)
U

U m cos t
Reatância resistiva: X R
R
0
 Fase: = 0
14
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 15

Corrente alternada num Indutor:
Figura 22 – Circuito AC com indutor. (a)
Gráficos de tensão e corrente versus tempo ediagrama de
fasores (b).
15

UL
Equações:
Um sen t
UL Um sen t
dI
dt
Um
sen t
L
dI
dt
Um
sen tdt
L
Um
sen
L
XL
 Reatância Indutiva:
IL


Um
cos t
L
IL
L
Fase:
t
2
L
= -900
UL adianta-se 900 em relação a IL
15
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 16

Corrente alternada num Capacitor
Figura 23 – Circuito AC com capacitor. (a) Gráficos de
tensão e corrente versus tempo ediagrama de fasores (b).
16

UC
Equações:
Q CUm sen t
IC
Um
Q
C
Um sen t
C cos
t

Reatância Capacitiva:


Fase:
IC
dQ
dt
Um
cos
XC
XC
t
2
1
C
= + 900
UC atrasa-se 900 em relação a IC
Recordar por:
ELI the ICE man…
16
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 17
Valores médios, máximos e eficazes
Como discutimos, uma tensão CA é aquela que
varia em módulo e sua polaridade varia
periodicamente, levando um intervalo de tempo T e
uma freqüência f. Pode ser produzida por um
alternador.
Figura 24 – Esquema do alternador e forma da
tensão produzida.
Podemos escrever o fluxo magnético sobre as
N espiras por:
N B A cos
t
B
: fase
Pela Lei de Faraday-Lenz:
B
t
N B A
t
t
sen
m
t
t
17
N B A
2
T
m
2
sen
f

1
T
f
Valores de tensão e corrente:
Uma onda CA de tensão ou de corrente possui
vários valores instantâneos ao longo do ciclo. São eles:
 Vm, Im: Valor máximo ou de pico. Aplicado
tanto ao pico negativo como ao pico positivo.
 Vpp ou Ipp: Vpp = 2 Vp = 2VM.
 Valor Médio: V Média sobre todos os valores
sobre uma onda senoidal em meio período.
1
T 2
V
1
T 2
V
Vm sen
V
 Valor
t dt
0
cos
2 Vm
T 2
T
V
V t dt
0
T 2
2 Vm
T
V
T 2
2
cos
Vm
rms
cos 0
V
(root
T
2
t 0
t
t
0.637Vm
mean
square):
Vrms
Quantidade de corrente ou tensão contínua capaz de
produzir a mesma potência de aquecimento. É definido
matematicamente por:
Esquemas de geradores AC e DC.
1
T
Vrms
Vrms
1
T
T
V t
2
dt
0
T
Vm sen
t
2
dt
0
T
Vrms
1 2
Vm sen2
T 0
t dt
17
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 18
Vrms
Vrms
T
1 2 1 cos 2
Vm
T 0
2
1 2
Vm
T
t
sen 2
2
2
t
t
dt
t
2
t 0
Vrms
Vrms
Vm
2
2
1 2
Vm
T
2
Vrms
18
0.707 Vm
18
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 19

Circuito
ca
R
ca
Lei de
Kirchhoff
Reatância
Um cos t RI(t)
Fase
Ief
(corrente
efetiva)
Im
(corrente
Máxima)
XR
Resumo:
L
ca
U m cos t
R
XL
C
ca
L
dI
dt
L
U m cos t
Q
C
XC
1
C
00
-900
+900
U ef
U ef
U ef
XR
Um
XR
XL
Um
XL
XC
Um
XC
19
(b)
Figura 25 -
19
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 20
Circuito RLC
Um importante circuito com muitas características
da maior parte dos circuitos ca é o circuito RLC em série
com um gerador. Discutimos esse circuito anteriormente
sem o gerador, e vimos que a corrente oscila com
frequência angular aproximadamente igual a
0
1
LC
A regra de Kirchhoff aplicada a este circuito
aplicada a esse circuito com gerador é:
Figura 26 -
dI
dt
L
Q
C
RI
U m sen t
ou
2
d I
dt 2
R dI
L dt
Um
sen t
L
1
I
LC
Esta equação diferencial é análoga à equação
do oscilador forçado, a primeira parcela é análoga à
m
d 2x
. A segunda parcela é análoga ao termo de
dt 2
amortecimento bv e o terceiro ao termo kx.
A solução desta equação é composta por dois
20
termos:
O primeiro termo, denominado transiente, que
chamaremos por IT, é solução da equação diferencial
homogênea associada:
d 2I
dt 2
R dI
L dt
1
I
LC
0
Sua solução já foi discutida no capítulo que
tratamos o circuito RCl. Assim:
IT (t )
e
R
t
2L
onde
( A cos[
t ] B sen[
n
t ])
R
4L2
2
0
n
n
A denominação de transiente provém deste
termo diminuir exponencialmente com o tempo.
O segundo termo é oscilatório e permanente e
não diminui exponencialmente com o tempo.
I
IT
I m sen( t
)
Quando t
o termo transiente da corrente
vai a zero e a solução pode ser dada por:
I
I m sen( t
)
Onde:
Im
Um
Z
Um
R
2
(XL
tg
XL
R2
(XL
X C )2
XC
R
O termo:
Z
X C )2
é denominado de impedância do circuito RLC e podese utilizar para análise o mesmo diagrama de fasores
dado anteriormente.
20
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 21
 Diagrama de Fasores de um circuito RLC:

Potência
A potência instantânea dissipada num resistor
é dada por:
Pode-se mostrar o diagrama de fasores de um circuito
RCL indicado pelos “vetores” UL ,UR , UC e U abaixo:
R I2
P
R I m2 sen 2 (
t)
Essa potência varia desde 0 até o valor
y
UL
RI m2 , conforme aparece na figura a seguir.
máximo
A maior parte de amperímetros e voltímetros medem os
valores médios quadráticos ou eficazes da corrente ou
da tensão. Define-se como valor médio eficaz como:
Um = Z Im
UR = R Im
t
I 2 Onde a corrente média quadrática é 21
I ef
dada por:
t-
T
1
T
I2
x
I 2 dt
0
2
I2
UC
Assim, da figura observa-se que:
Um
U
2
R
(U L
UC )
I m2
sen 2 ( t )dt
2
0
2
2
I2
I m2
2
0
Veja que:
Um
ZI m
Im
Um
Z
Um
Im
R2
( L
1 2
)
C
Observe que a corrente será máxima para a
frequência da fonte for igual à frequência de ressonância:
0
1
, quando isso ocorrer, a
LC
impedância Z será mínima e Z = R.
Essa condição de ressonância é a mesma de um
oscilador harmônico forçado. Na ressonância, =00 e os
fasores UL=UC. A corrente está em fase com a força
eletromotriz aplicada.
I
2
I
2
m
1 cos( 2 t )
dt
2
1 sen(2 t )
t
2
4
2
2
0
Para a potência média, sobre um ciclo completo,
teremos:
I m2
I2
2
I 2 teremos:
Como I ef
I ef
I m2
2
Im
2
I ef
A potência média fornecida pelo gerador é
igual à dissipada pelo resistor.
Pmed
U I
Pmed
Pmed
R I2
med
R I m2
2
Um I m
2
Uef I ef
Analogamente:
U ef
U m2
2
U ef
Um
2
21
med
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 22
Potência instantânea P(t) e Potência média
Figura 27 -
Pmed
A potência instantânea fornecida pelo gerador
num certo instante é dada por:
P(t) UI Um sen tIm sen( t
)
P(t) UmIm sen t sen( t
)
Desenvolvendo a expressão teremos:
P(t) UmIm sen t(sen t cos
P(t ) U m I m (sen
2
t cos
sen cos t)
sen sen t cos t )
22
Quando fazemos a média temporal sobre o
período T (T=2 / ) da potência instantânea, temos a
potência média, que denominaremos por Pmed. Assim:
P(t ) U m I m (sen 2 t cos
sen sen t cos t )
T
1
P (t )dt
T 0
Pm ed
Observe que apareceram duas integrais, cujos
valores são 0 (funções par e ímpar integradas num
período)e ½ (como demonstrado anteriormente):
T
1
sen t cos tdt
T 0
T
1
sen 2 tdt
T 0
0
1
2
Assim, a potência média dará:
Pmed
1
U m I m cos
2
Ou
Pmed
U ef I ef cos
No diagrama de fasores, veja que o triângulo
fornece:
cos
tg
UR
U
XL
R
Z
Xc
Z
Como Uef = Z Ief
Substituindo na equação da Potência média,
teremos:
Pmed
Potência média versus freqüência angular.
U ef
U ef R
Z Z
U ef2
R
Z2
22
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 23
R
U ef2
Pmed
1
C
L
0
2
R2
Chamando de:
Podemos ainda escrever, dividindo e multiplicando
por L o termo ( )2:
1
2
Pmed
U ef2 R
2
(
R
2L
R
e
2L
0
2
A largura será dada por:
2 2
0
2
)
R
R
2L
0
2
1
2
Em analogia à Mecânica, esta equação mostra que
o fornecimento médio de potência do gerador é o mesmo
que o de um oscilador forçado, com R no lugar do
amortecimento b, L no lugar da massa m e Uef substituindo
a força motriz máxima F0.
O gráfico abaixo mostra a potência média em
função da frequência no caso de valores de resistência R
grande e pequeno.
R
L
23
Definimos a largura de ressonância por um
parâmetro adimensional, que chamamos de Q do
circuito, definido pela razão entre a frequência de
ressonância e a largura da curva:
Q
L 0
R
0
Note que para R pequeno temos fator Q grande
e vice-versa.
Uma aplicação comum nos circuitos de
ressonância em série encontra-se nos receptores de
rádio, onde se varia a frequência de ressonância do
circuito mediante a variação da capacitância. A
ressonância ocorre quando a frequência natural do
circuito for igual à frequência das ondas de rádio
captada pela antena.
Quando
L2
2 2
0
2
2
R2
U ef2
Pmed
R
Ou seja, a potência terá a metade de seu valor
máximo. Podemos estimar que isso ocorrerá para as
frequências:
L
L
2
2
0
R
0
0
Na
ressonância,
há
uma
corrente
relativamente grande no circuito da antena. Se o valor
Q for suficientemente elevado, as correntes devido às
outras estações transmissoras, fora da ressonância,
terão valor desprezível em comparação com as da
estação na qual o circuito está sintonizado.
0
X C1
1
C
X C2
1
C
R
0
L(
Exemplo 9 – Um capacitor de 20 F está
ligado a um gerador de força eletromotriz máxima de
100 V. Calcular a reatância e a corrente máxima
quando a frequência for de 60 Hz e 5000Hz.
)
0
R
I m1
Assim:
0
R
2L
I m2
2
2
Um
X C1
Um
X C2
1
60 20 10 6
133
1
1,59
5000 20 10 6
100
0,754 A
133
100
1,59
62,8 A
23
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 24
Exemplo 10 - Um circuito RCL em série, com L =
2H, C = 2 F e R = 20 está alimentado por um gerador de
fem máxima de 100 V e frequência variável. Determinar
quando a frequência angular do gerador for de
= 400
rad/s:
(a) A frequência de ressonância
(b) A fase
(c) Acorrente máxima Im.
0
.
1
1
1250
C 400 2 10 6
XL
L 400 2 800
Para calcular a impedância, o valor de XL – XC é
muito maior que R nas condições afastadas da ressonância.
Então teremos para a Impedância Z:
(a) X
C
Z
(b) tg
(c) I m
(XL
X C )2
X L Xc
Z
Um
Z
R2
450
20
450
22,5
100
0,222A
450
870
c)
O Transformador:
O transformador básico é formado por duas
bobinas isoladas eletricamente e enroladas em torno de
um núcleo comum. Para transferir energia elétrica de
uma bobina para outra se usa o acoplamento magnético.
A bobina que recebe energia da fonte de corrente
alternada é chamada de primário. A bobina que
fornece energia para uma carga é chamada de
secundário.
Os núcleos dos transformadores usados em
aplicações de baixa freqüência são feitos geralmente de
material magnético, de aço laminado. Os núcleos dos
24
transformadores de uso em altas freqüências são feitos
de ferro em pó e cerâmica ou de materiais não
magnéticos. Algumas bobinas são enroladas em torno
de formas ocas não magnéticas, como por exemplo
papelão ou plástico, de forma que o material que forma
o núcleo é o ar.
Figura 28 – Esquema de transformadores:
Vp
 Relação:
Vs
Vp
Np
Vp
Vs
Ns
Vs
Is
Ip
Onde:
Vp: Tensão na bobina do primário.
Vs: Tensão na bobina do secundário.
Np: Número de espiras da bobina do primário.
Ns: Número de espiras da bobina do
secundário.
Especificações: kVA.
Figura 29 – Esquema do núcleo do transformador.
24
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 25
Figura 30 – Aplicações, modelos e representação.
Portanto, a fim de transportar potência com
mínima perda de calor RI2 nas linhas de transmissão, é
econômico usar tensão elevada e corrente baixa.
Por outro lado, considerações de segurança,
por exemplo, isolamento, tornam conveniente o uso de
tensão baixa e corrente alta para operar motores e
outros aparelhos elétricos. Consegue-se esse efeito
usando-se um transformador, dispositivo que modifica
a voltagem alternada e a corrente alternada sem
perda apreciável de energia.

Símbolo:
trafo
25
Sendo V a voltagem e I a corrente, a potência
instantânea é VI. Se a voltagem for modificada, sem
alteração na potência, a corrente também deve ser
modificada. A figura abaixo mostra o diagrama de um
transformador simples, constituído por duas bobinas
enroladas num núcleo comum de ferro doce.
A bobina que recebe energia é o primário e a
outra bobina é o secundário. Qualquer uma das duas
bobinas do transformador pode ser usada como
primário ou secundário.
A função do núcleo de ferro é aumentar
grandemente o fluxo, para uma dada corrente, e
confiná-lo de modo que quase todo o fluxo que passa
por uma bobina passe pela outra. O núcleo de ferro é
laminado para evitar perdas pelas correntes de Foucault
(correntes circulantes, provocadas por fluxos variáveis).
Outras perdas possíveis estão nas resistências
das bobinas (RI2), que podem ser reduzidas usando-se
fios de baixa resistência nas bobinas e perdas por
histerese no núcleo, que podem se reduzir usando
núcleos de ferro doce.
É relativamente fácil projetar um
transformador em que a potência é transferida do
primário ao secundário com eficiência de 90 a 99%.
Discutiremos a seguir um transformador ideal,
no qual não há perdas de energia.
A força eletromotriz induzida no primário é
dada por:
V1
N1
d
esp
dt
O fluxo no secundário, admitindo não ocorrer
fugas para fora do núcleo, é dado por:
V2
N2
d
esp
dt
Assim, teremos a relação:
V2
N2
V1 ou
N1
25
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 26
com a mesma taxa de variação, isto é, o fluxo no núcleo
de ferro deve continuar o mesmo como se não houvesse
a resistência de carga ligada ao secundário.
Então, o primário puxa da fonte uma corrente
adicional I1 a fim de manter o fluxo original esp. O
fluxo através de cada espira, provocado por esta
corrente adicional, é proporcional a NpIp. Então a
corrente adicional no primário Ip está relacionada à
corrente Is no secundário por:
NS
VP
NP
Vs
Figura 31 – Esquema.
NpI p
Aplicando a Lei de Kirchhoff no primário,
teremos:
d
dt
d
dt
O sinal negativo indica que as correntes estão
defasadas 1800, em virtude de provocarem fluxos
26
opostos. Uma vez que Is está em fase com Vs, a corrente
adicional no primário Ip está em fase com a fem
aplicada.
A figura a seguir mostra as relações de fase
entre as tensões e as correntes.
A corrente total no primário é a soma
“vetorial” entre a corrente de magnetização original Im
e a da corrente adicional Ip, que usualmente é muito
maior que Im.
0
V1
Vp
I1= Ip
Então:
Vs
V2
I
N2
N1
Im
O transformador é denominado de alta se :
Ns
N p ; N2
N p ; N2
N1
ou seja, a tensão de saída é menor que a tensão de
entrada.

I2=Is
N1
ou seja, a tensão de saída é maior que a tensão de
entrada.
O transformador é denominado de baixa se :
Ns
Ns Is
Corrente elétrica no transformador
Não há corrente no secundário quando este circuito
está em aberto. A corrente Im é muito pequena no primério e
está defasada de 900 com a tensão. Nesta bobina.
Considere agora o que ocorre quando ligamos uma
resistência de carga no secundário. Haverá uma corrente I2
no circuito secundário que estará em fase com a tensão V 2
na resistência. Esta corrente estabelece um fluxo adicional
em cada espira ’esp proporcional a NsIs. Este fluxo
superpõe-se ao fluxo esp estabelecido pela corrente de
magnetização original no primário, Im. No entanto, a
voltagem do enrolamento primário está determinada pela
fem do gerador, que não é afetada pelo enrolamento no
secundário. O fluxo no núcleo de ferro doce deve continuar

Potência no transformador:
A potência fornecida pelo gerador é o produto
da força eletromotriz eficaz aplicada pela corrente
eficaz Ief no primário e pelo fator de potência cos ,
onde este é o ângulo de fase entre a corrente total I e a
fem aplicada. Como Ip está em fase com a fem aplicada,
é o ângulo entre Ip e I. Note que Icos é igual à
corrente adicional Ip, de modo que a injeção de potência
no primário é:
P
I ef
ef
cos
ef
I pef
Usando as relações anteriores, teremos:
Ip
Np
Vs
Ns
IS
Np
I p,ef
Vs ,ef I s ,ef
Ns
Vs I s
Então:
ef
26
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 27
A potência despendida no primário é igual à saída
de potência no secundário, como se admitiu no
transformador ideal sem perdas.
Na maior parte dos casos, a corrente Ip no primário
é muito maior que a corrente de magnetização inicial I m,
sem carga. O que se pode demonstrar colocando em série
uma lâmpada com o primário: a lâmpada brilha muito mais
quando há carga no secundário do que quando o secundário
está em aberto. Se Im puder ser desprezada, a relação:
Np Ip
Ns I s
dá a lei das correntes totais no primário e no secundário.
As correntes Is e Ip podem ser relacionadas com a
resistência de carga por:
27
Vs
R
Is
Como:
NS
VP
NP
VS
NS
NP
e:
Ns
Is
NP
Ip
NS VS
NP R
NS
2
NS NP
NS
Ip
NP
R
NP
R
Pode-se escrever a corrente no secundário e sua
tensão em termos da corrente no primário e da força
eletromotriz no primário, . Assim:
Ip
2
Np
R
Ns
A corrente Ip é a mesma que circularia se estivesse
ligada ao gerador a resistência:
Np
Ns
2
R
Esse efeito é denominado de transformação de
impedância, pois em geral a carga no secundário é
constituída de uma combinação de capacitâncias,
indutâncias e resistências, com impedância Z, ligadas ao
secundário do transformador.
27
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 28
Motores elétricos
O motor é uma máquina que transforma a energia
elétrica em energia mecânica.
O princípio de funcionamento do motor elétrico,
baseia-se na indução eletromagnética. Todo condutor,
quando percorrido por uma corrente elétrica, apresenta um
campo magnético que o circunda. Se este condutor for
colocado ao lado de um outro que apresenta também um
campo magnético, então os dois campos interagirão entre si
atraindo ou repelindo de acordo com o sentido da corrente
elétrica que o percorre.
Classificação dos motores:
Podemos classificar em dois grupos:
 Motor de corrente contínua simples
28
Figura 31 – (a) Esquema de motor de corrente
contínua.
(b) Motor síncrono.
Um único motor elétrico pode ser alimentado
por uma bateria ou um pequeno gerador. Porém, é
indispensável numa rede de alimentação em escala
nacional para fornecer energia aos milhões de unidades
de potência elétrica instalada e que são convertidos em
energia mecânica nas linhas de montagem de
automóveis, nas máquinas de mineração, nas
locomotivas elétricas, etc. Apesar dos automóveis,
28
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 29
navios, locomotivas a diesel, caminhões e aeroplanos não
dependerem de energia da rede elétrica, todos utilizam
motores elétricos, que são partes essenciais em
condicionadores de ar, refrigeradores, máquina de lavar,
etc.
Discutiremos os diversos tipos de motores
detalhadamente a seguir.
Os motores simples, de corrente contínua
(cc), é mostrado na figura (a). A corrente da bateria
magnetiza a armadura em ferro doce que pode girar em
torno do eixo AA´, e tende a se alinhar com o campo
magnético produzido pelo ímã de pólos N e S. Quando a
armadura gira, arrasta consigo o comutador, cujos
segmentos invertem a direção da corrente no instante em
que a armadura atinge sua posição de equilíbrio. A inércia
da armadura assegura a continuação do movimento além da
posição de equilíbrio; então, graças à inversão de
polaridade, há uma nova rotação de meia volta. Uma vez
que o comutador inverte a direção da corrente a cada 180º,
consegue-se a rotação contínua. O eixo do motor pode
então fornecer um trabalho útil.
 DESVANTAGENS:
1.
Quando a corrente é desligada, o motor tem
a tendência de parar na posição de equilíbrio e, por isso,
pode não haver um torque de partida.
2.
O torque é nulo duas vezes a cada volta. Se
a armadura tiver pólos e enrolamentos adicionais, e se o
comutador for dividido em maior números de segmentos, o
torque é mais uniforme e o motor sempre dá a partida.
Quando o campo for originado por um ímã
permanente, como nos trens de brinquedo e na maior parte
dos brinquedos operados por pilha, a velocidade depende da
tensão de alimentação e se modifica com a carga.; Nas
aplicações em que são necessárias quantidades
significativas de potência, o campo é provocado por
eletroímãs. A ajustagem da corrente do campo possibilita
controlar a velocidade, independentemente da corrente na
armadura. Em geral, quando a carga num motor cc
aumenta, a velocidade diminui e é preciso aumentar a
corrente da armadura. A corrente de campo pode ser
ajustada a fim de manter a velocidade constante. Nos
motores cc usam-se freqüentemente controles automáticos
desses parâmetros.
Os motores cc com bobinas de campo são muito
flexíveis. Podem ser ligados em série, de modo que a
corrente na armadura é também a corrente de campo, em
paralelo (ou em shunt), de modo que a corrente de campo
seja independente da corrente da armadura, ou em ligação
composta, com duas bobinas de campo, uma ligada em
série e outra em paralelo. Esses motores são amplamente
utilizados para tração (em metrôs e trens elétricos) e em
aplicações onde o controle de velocidade seja crítico.
O motor cc torna-se um motor síncrono quando o
comutador for substituído por um anel contínuo (b) e a
alimentação for corrente alternada. Apesar de este
dispositivo simples não Ter torque de partida, uma vez
acelerado por um meio externo, opera em fase com
uma velocidade síncrona, (determinada pela frequência
da linha de alimentação). Quando a carga aumenta, a
corrente na armadura aumenta, mas a velocidade
permanece constante, a menos que a carga seja
suficientemente grande para fazer o motor estancar. Os
motores síncronos projetados para corrente trifásica
podem ser autoderramantes. Quando a potência é
elevada, a corrente de campo é muito menor que a da
armadura. Para que se possa injetar a pequena corrente
através dos anéis coletores, a maioria desses motores
têm uma armaduraestacionária quando o campo gira
29
com o eixo que aciona a carga.
O motor universal em série tem muitas
aplicações em dispositivos de pequena potência, como
furadeiras manuais e pequenas serras.
Praticamente, quase toda a potência elétrica
fornecida nas redes comerciais é trifásica, com tensão
senoidal em 60Hz. O termo trifásico significa que
existem três tensões senoidais de igual amplitude e
frequência, cujos picos sucessivos são separados por
um terço de ciclo. As três tensões são usualmente
conduzidas por uma linha de transmissão em três
condutores, comumente visíveis nas redes urbanas.
Existe uma fase de potência entre cada par de
condutores. As residências são, quase sem exceção,
abastecidas por uma única fase; as indústrias recebem,
comumente, todas as três.
No motor de indução trifásico, as bobinas de
cada três pares de pólos estão ligadas a fases diferentes.
As correntes nas bobinas, por isso atingem valores
máximos sucessivamente, e o resultado é um campo
magnético girante na região entre os pólos. Um rotor
estacionário, de material condutor, teria corrente
induzidas caso estivesse imerso nesse campo. O campo
magnético das correntes induzidas interagiria com o
campo girante para provocar um torque. Caso não haja
carga, o torque acelera o rotor até uma velocidade
29
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 30
quase igual à velocidade síncrona da de rotação do campo.
(Caso o rotor atinja a velocidade síncrona, desapareceria o
movimento relativo entre o rotor e o campo, não existiriam
correntes e, por isso, desapareceria também o torque).
Quando o motor está em carga, a velocidade do rotor
diminui, isto provoca uma corrente induzida maior e,
correspondentemente, maior torque. A velocidade pode
diminuir a 75% da velocidade síncrona antes de o motor
estancar. Não existem contatos elétricos móveis no motor
de indução trifásico, que pode ser construído para Ter
centenas de cavalos de potência. A eliminação de qualquer
possibilidade de centelhamento torna estes motores
especialmente atrativos para aplicações atmosferas
explosivas, como em moinhos de trigo ou em minas.
O motor de indução prático, tem, usualmente, um
rotor cilíndrico de ferro, com barras isoladas de cobre
embutidas na superfície e ligadas de modo a oferecer bons
circuitos condutores às correntes induzidas. Em alguns
motores o enrolamento do rotor, em lugar de estar em curto,
é ligado a anéis coletores, de modo que se possam usar
resistores para controlar a velocidade.; os contatos móveis
assim existentes eliminam uma vantagem importante do
motor.
Caso apenas uma fase esteja ligada, não há campo
magnético girante e não há torque de partida. Porém se uma
segunda bobina for ligada em série com um capacitor de
grande capacitância (centenas de microfarads) e for
alimentada pela mesma fase que a da primeira bobina, as
correntes nas duas estarão suficientemente defasadas para
provocar o campo magnético girante e fornecer o torque de
partida. É este dispositivo empregado nos motores de
indução monofásicos, que se usam nos refrigeradores,
máquinas de lavar roupa, condicionadores de ar e
ventoinhas dos fornos.
.
Referência: Texto e figura adaptados e extraídos
de: Física - Paul Tipler, V2 pg794-796 Editora Guanabara
Dois.
A seguir discutiremos detalhadamente a ação
do motor e os tipos de motores.

Ação do Motor:
A força eletromagnética que atua num
condutor é dada por:
F
BIlsen
Quanto a construção, o motor elétrico dividese basicamente em duas partes, o Rotor e o Estator.
30
O rotor ou induzido, é a parte girante do motor
e o estator ou indutor é a parte fixa do mesmo.
Os motores elétricos são divididos em três
segmentos:
(a) Motores de corrente contínua;
(b) Motores de corrente pulsante(motor de
passo);
(c) Motores de corrente alternada.
Os motores de corrente contínua subdividemse em ímã permanente, ligação série, paralelo (shunt) e
misto(compound).
Em corrente alternada, os motores dividem-se
em três sistemas, monofásico, linear e trifásico. Para
nosso estudo, analisaremos os monofásicos e trifásicos.
Tanto os motores monofásicos quanto os trifásicos
dividem-se em dois segmentos, os motores síncronos e
os assíncronos.
 Motores monofásicos assíncronos (indução):
(a) Rotor bobinado: repulsão, partida à
repulsão e repulsão indução.
(b) Rotor gaiola de esquilo: fase dividida,
capacitor de partida, capacitor permanente, duplo
capacitor e campo distorcido.

Motores monofásicos síncronos: ímã
permanente, histerese, relutância e indutor.

Motores trifásicos assíncronos(indução):
rotor bobinado e gaiola de esquilo.

Motores
trifásicos
síncronos:
ímã
permanente, rotor bobinado e relutância.
Em nosso estudo, trataremos dos seguintes
tipos de motores:
a) Motores de corrente contínua de ímã
permanente, série, paralelo e misto.
b) Motores de corrente alternada monofásico
de repulsão, indução, partida capacitiva e polo partido.
c) Motor de corrente alternada trifásico rotor
gaiola de esquilo.
d) Motor monofásico universal.
Começaremos o estudo experimental com os
motores de corrente contínua.
30
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 31
 Motor de ímã permanente: Neste motor, teremos
dois ímãs onde cada um apresentam uma superfície com um
polo norte e um polo sul. Fixando sobre este ímã uma
sapata polar (material ferromagnético), podemos criar um
campo norte e um campo sul mais intenso de acordo com
posicionamento destes ímãs.
É convencionado a utilização da cor azul para
identificar o polo sul e a cor vermelha para o polo norte.
Com isso teremos, de acordo com a figura mostrada, a
 Exemplo 2 – Um campo magnético uniforme faz
um ângulo de 300 com o eixo de uma bobina circular de 300
espiras com 4 cm de raio. O campo está variando à razão de
85 T/s. Determine o módulo da tensão induzida na bobina.

Solução: Pela Lei de Faraday:
d
m
dt
maioria das linhas de campo saindo do polo
norte e chegando ao polo sul.
d
N B A cos
dt
N A cos
300 0.042 cos30 85
111V

 Exemplo 3 – Um campo magnético B é
perpendicular ao plano do papel e uniforme em uma
região circular de raio R. Do lado de fora da região
circular

 dB
B é nulo. A taxa de variação de B 31.
dt
Determine o módulo do campo elétrico induzido
(a) a uma distância r < R do centro da região
circular.
(b) a uma distância r > R onde B = 0.
Referências
1. http://pt.wikipedia.org/wiki/Página_principal
Exemplos Resolvidos – Tipler
 Exemplo 1 – Determinar o fluxo magnético
através de um solenóide de 40 cm de comprimento, 2.5 cm
de raio e 600 espiras, percorrido por uma corrente de 7.5A.

Solução:
r2
A
m
A
N B A
m
0.0252
N
N 0
I
l
 Solução: Pela Lei de Faraday:
(a)
d
N
I
r2
l
6002
4 10 7
7.5
0.0252
0.4
1.66 10 2Wb
m
m
0
 Exemplo 2 – Um campo magnético uniforme faz
um ângulo de 300 com o eixo de uma bobina circular de 300
espiras com 4 cm de raio. O campo está variando à razão de
85 T/s. Determine o módulo da tensão induzida na bobina.

Solução: Pela Lei de Faraday:
d
m
m
dt
N B A cos

E
m
dt
 
 E dl
r2

dl
C
E 2 r
C
2
m
dB
dt
d
m
dt
d B A
r2
dt
dB
dt
dB
dt
r 2 dB
r dB
E
E
;r R
2 r dt
2 dt
d m d B A
dB
R2
(b)
dt
dt
dt
dB
E 2 r
R2
dt
2
R dB
E
;r R
2 r dt
E 2 r
r2
31
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 32

 Exemplo 4 – Um campo magnético uniforme B é
aplicado a uma bobiba de N espiras. A bobina está ligado a
um integrador de corrente ©, um dispositivo capaz de medir
a carga total que o atravessa. Determine a carga que
atravessa a bobina quando ela sofrer uma rotação de 180°
em torno de seu diâmetro.

dQ
Q
I
Idt
R
d
m
dt
d
dB
dt N
r2
dB
1
I R
dt N
r2
dB
1
4 30
dt 80
0.052
dB
T
191
dt
s
d m
1
dt Q
dt
R
1
Q
mf
mi
R
1
Q
NBA
NBA
R
2N B A
Q
R
1
R
m
 Solução:
(a) I = 0 pois o fluxo não varia!
(b) m N B A
N
m
d
Solução:
m
N B A
m
N B
m
dt
r2
m
B
dB
dt
32
m
 Exemplo 5 – Uma bobina de 80 espiras tem 5 cm
e sua resistência é de 30 . Qual deve ser a taxa de variação
de um campo perpendicular para que a corrente induzida na
espira seja 4.0 A ?

m
dt
1
dt dt
R
Q
Q
d
 Exemplo 6 – Uma bobina retangular de 80
espiras, 20 cm de largura e 30 cm de comprimento, é
submetida a um campo magnético B = 0.8 T dirigido
para dentro do papel, com apenas metade da bobina na
região em que existe campo magnético, que se extende
indefinidamente para a esquerda e direita. A resistência
da bobina é de 30 . Determinar o módulo, a direção e
o sentido da corrente induzida se a bobina está se
movendo com uma velocidade de 2 m/s
(a) para a direita;
(b) para cima;
(c) para baixo.
Solução:
Q
Pela Lei de Faraday:
N
1
N
r2
d m
2
r dt
d
I
m
dt
R
B 20 x
dx
N B 20
dt
d m
R I
dt
dx
N B 20
dt
I
R
32
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 33
I
0.853A
F
A corrente está no sentido anti-horário.
(c) A corrente será a mesma que em (b) porém no
sentido horário.
I
 Exemplo 7 – No esquema da figura, faça B = 0.6 T
,v = 8m/s, l = 15 cm e R = 25 ; suponha que a resistência
da barra e dos trilhos possa ser desprezada. Determine:
(a) a tensão induzida no circuito;
(b) a corrente no circuito;
(c) a força necessária para fazer com que a barra se
desloque com velocidade constante.
(d) a potência dissipada no resistor.
 Solução
(a)
m
dt
1
(b)
I
(c)
F
(d)
P
R
I
I
I Bl
F
R I2
N B l
dx
dt
N B l v
0.6 0.15 8
0.72V
0.72
25
28.8mA
F 0.0288 0.6 0.15
2.59mN
20.7mW
Ou
P F v 20.7mW
 Exemplo 8 – Uma barra de massa m desliza sem
atrito sobre trilhos condutores em uma região onde existe
um campo magnético uniforme constante . No instante t =
0, a barra está se movendo com velocidade inicial v0 e a
força externa que agia sobre ela é removida. Determine a
velocidade da barra em função do tempo.

Solução
F
m a
F
m
dv
dt
I
R
R
33
F
d
I Bl
Bl v
B l v
I
R
B l v
I B l
F
B l
R
B2 l 2 v
F
R
dv
B2 l 2 v
m
dt
R
2
2
dv
B l
dt
v
m R
v
t
dv
B2 l 2
dt
v
m R 0
v0
ln v ln v0
B2 l 2
t
m R
v t
v
v0
ln
v0 e
B2 l 2
t
m R
B2 l 2
t
mR
 Exemplo 9 – Determine a auto-indutância de
um solenóide de comprimento l = 10 cm, área 5 cm2 e
100 espiras.

Solução
L
0
n2 A l
2
L 4
100
10
5 10
0.1
L 6.28 10 5 H
7
4
0.1
 Exemplo 10 – Uma certa região do espaço
contém um campo magnético de 200 G e um campo
elétrico de 2.5.106 N/C. Determine:
(a) a densidade de energia na região.
(b) a energia contida em uma caixa cúbica de lado
l = 12 cm.
33
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 34

Solução:
Densidade de energia elétrica:
1
2
ue
0
 Exemplo 12 – Determine o calor total
produzido pelo resistor R da figura quando a corrente
no indutor diminui do valor inicial I0 até 0.
E2
1
8.85 10 12 2.5 106
2
J
ue 27.7 3
m
ue
2
Densidade de energia magnética:
1 B2
2 0
um
34

1 0.022
2 4 10 7
J
um 159 3
m
um
P
Solução:
dW
dt
dW
I (t )
u ue um
u 27.7 159
J
u 187 3
m
W
u l3
U
U
U
R I0 e
R I 02 e
W
2
R
t
L
dt
2R
t
L
dt
0
t
187 0.123
0.323J
W
 Exemplo 11 – Uma bobina de auto-indutância 5.0
mH e resistência 15.0
é ligada aos terminais de uma
bateria de 12 V cuja resistência interna é despresível.
(a) Qual é a corrente final?
(b) Qual a corrente após 100 s?

I0 e
R
t
L
0
Energia no interior da caixa:
u V
R I 2 (t )dt
W
0
Densidade de energia:
U
P dt
Solução:
W
R I 02
e
2R
t
L
2R
L
t 0
R L 2
I0 0 1
2R
L I 02
W
2
t
(a) I (t )
If
L
R
Com
If
(b)
 Exemplo 13 – Determine o valor das correntes
I1, I2 e I3:
(a) imediatamente após a chave S ser fechada;
(b) um longo tempo após a chave S ser fechada.
Depois de permanecer fechada por um longo tempo, a
chave S é aberta. Determine as três correntes
(c) imediatamente a chave S ser aberta;
(d) um longo tempo após a chave S ser aberta.
1 e
0
R
L
R
If
12
15
I f 0.8 A
5 10
15
3
I (t 100 s )
333 s
0.8 1 e
I (t 100 s)
100
333
0.207 A
34
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 35
 Solução:
(a) A corrente através do indutor é zero, antes da
chave ser fechada. Assim:
I1
I2
150V
10
20
I3
I1
I2
5A
I1
1
20
Req
10
(c) Quando a chave é reaberta, I1 deve ser 0 e a
corrente no indutor permanece I3 = 3.75A.
I2 = - I3 = -3.75A.
(d) Depois de um longo tempo que a chave é
aberta, as correntes são nulas
I3
0A
 Exemplo 14 – Uma bobina de 250 voltas e 3 cm2
de área gira a 60 Hz sob um campo magnético uniforme de
0.4T. Qual a fem máxima produzida?

Vrms
12 2.832
Pav
1
20
I2
Vrms
R
Vp
48
Vrms
Vrms 33.9411V
2
2
33.94
35
Irms
12
Irms 2.83A
2
(b) Potência média: Pav R I rms
I rms
150V
I1 7.5 A
10
10
I2 I3 3.75A
I1
 Solução:
(a)
0A
(b) depois de um longo tempo, a corrente se
estabiliza e o indutor atua como um curto circuito.
1
Req
(a) A corrente rms.
(b) a potência média.
(c) a máxima potência.
Pav 96W
2
(c) Potência máxima: Pmax R I max
Vmax
I max
R
48
I max
I max 4 A
12
Pmax 192W
 Exemplo 16 – Encontre:
(a) a corrente média Im.
(b) a corrente rms Irms. A função da corrente com o
tempo é dada por:
I (t ) I 0
t
T
Solução:
d
m
dt
d
N B A cos
dt
N B A
sen
t
t
N B A
N B A2 f
m
250 0.4 3 10 4 2 60
 Solução:
(a)
m
m
m
11.3V
Im
I av
I av
1
T
1
T
T
T
I0
0
I (t )dt
0
t
dt
T
 Exemplo 15 – Um resistor de 12Ω está conectado
a um gerador AC de pico 48 V. Encontre:
35
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 36
T
I0
T2
I av
tdt
I0 t 2
T2 2
I av
0
I av
t T
t 0
I max1
(b) X L2
L
2
X L2
I0 T 2
T2 2
I0
Iav
2
X L2
2
I
1
T
I
T
1
T
I
2
0
T
t
I0
T
0
___
2
I 02
T3
___
2
2
0
3
I
I
T
I
I max2
I (t ) dt
I max 2
2
dt
t 2 dt
0
t T
t 0
3
I 02 T
I
T3 3
___
I 02
I2
3
___
2
___
2
I rms
I
I rms

Solução:
(a)
X C1
X C1
X C1
I 02
3
2
X C1
I max1
3
 Solução:
(a) X L1
1 L
X L1
I max1
I max1
(b)
2
X L1
15.1
I max1
Vmax
X L1
I max1
120
15.1
36
1
2 f1 C
1
60 20 10 6
133
Vmax
X C1
100
133
0.752 A
C
1
2 f2 C
1
2 2000 20 10 6
X C2 1.59
Vmax
I max 2
X C2
X C2
f1 L
60 40 10
120
503
0.239 A
1
X C2
2
2
Vmax
X L2
C
1
 Exemplo 17 – Um indutor de 40 mH é ligado a um
gerador AC que possui fem máxima de 120 V. Encontre a
reatância indutiva e a corrente máxima nas freqüências:
(a) f 1 = 60 Hz
(b) f 2 = 2000 Hz.
X L1
503
1
I0
I rms
3
 Exemplo 18 – Um capacitor de 20 µF é
colocado com um gerador de CA com tensão máxima
de 100V. Encontre a reatância capacitiva e a máxima
corrente quando a freqüência for de:
(a) f 1 = 60 Hz (b) f 2 = 2000 Hz.
T
t3
3
f2 L
2000 40 10
I max 2
___
2
___
2
2
X L2
___
2
(b) I rms
7.95 A
3
X C2
36
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 37
I max2
I max 2
100
1.59
62.9 A
 Exemplo 19 – Um capacitor de capacitância
eletrostática C = 20 µF é carregado a 20 V e colocado com
um indutor de indutância L = 6 µH.
(a) Qual é a freqüência de oscilação?
(b) Qual a máxima corrente?
37

Solução:
(a)
f

Solução:
(a)
f
2
f
2
f
f
2
f
(b) I max
f
1
L C
1
2 L C
1
6 10 6 20 10
4.59 104 Hz
Q0
I max
6
1
Q0
L C
Q0
I max
C V0
C V0
I max
L C
20 10 6 20
6 10 6 20 10
Imax 11.5A
6
 Exemplo 20 – Em um circuito RLC, R = 20 Ω, a
capacitância eletrostática C = 2 µF e a indutância do indutor
vale L = 2 H. O valor máximo da fem do gerador é max =
100V.
(a) Qual é a freqüência de ressonância f0?
(b) Qual o valor do fator Q?
(c) Encontre a largura de ressonância f.
(d) Qual o máximo valor de corrente na ressonância?
1
L C
1
2 L C
1
2 2 2 10 6
f 79.6Hz
0 L
(b) Q
R
2 f L
Q
R
2 79.6 2
Q
20
Q 50
f0
79.6
(c) f
f
Q
50
f 1.59Hz
Emax
(d) I max
R
100
I max
Imax 5 A
20
 Exemplo 21 – Em um circuito RLC, R = 20 Ω,
a capacitância eletrostática C = 2 µF e a indutância do
indutor vale L = 2 H. O valor máximo da fem do
gerador é max = 100V e a freqüência do gerador é f =
60 Hz.
(a) Qual é a máxima corrente Imax?
(b) Qual o ângulo de fase ?
(c) O fator de potência.
(d) A potência média liberada?
37
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 38
Pav
0.305W
 Exemplo 22 – Em um circuito RLC, R = 20 Ω,
a capacitância eletrostática C = 2 µF e a indutância do
indutor vale L = 2 H. O valor máximo da fem do
gerador é max = 100V e a freqüência do gerador é f =
60 Hz.
Encontre o valor máximo da voltagem no resistor,
do indutor e do capacitor na freqüência de ressonância.
 Solução:

Solução:
(a)
I max
VR ,máx
VL,máx
max
XL
Z
X R2
Z
R2
Z
R2
Z
Z
20
XL
2
Z
f L
60 2
202
VC ,máx
1
f C
2
754 1326
1
XC
2
1
60 2 10
2
L
XL 2
X L 1000
VL ,máx 5000V
2
0
f0 L
XC
1
f0 L
2
1000
VC ,máx
2
X C I máx
XC
C
38
X L I máx
0
2
1
C
L
2
2
Xc
R I máx
5000V
6
2
Z 572
max
I max
Imax
Z
100
572
Imax
0.175 A
(b) ângulo de fase:
XL
tg
Xc
R
754 1326
tg
20
tg
28.6
88
 Exemplo 23 – Um resistor R e um capacitor C
estão ligados em série com um gerador . A tensão do
gerador é dada por:
Vent
V0 cos
t
Determine o valor rms da tensão entre os
terminais do capacitor, Vsai,rms em função da freqüência
angular .
(c) Fator de potência:
cos
0.0349
(d) Potência média:
Pav
Pav
Pav
1
2
1
2
R I max
2
0.306W
max
Imax cos

Solução:
Vsai ,rms
X C I rms
38
Física III – Prof. Dr. Cláudio S. Sartori - CAPÍTULO VI – Lei de Faraday e Indução Eletromagnética 39
Vent , rms
I rms
Z
Z
R2
Vsai ,rms
XC
Vsai ,rms
XC
1
C
1
C
Vsai ,rms
1
C
Vsai ,rms
Vsai ,rms
X C2
Vent ,rms
Z
Vent ,rms
XC
Vsai ,rms
V2 I 2 V1 I1
R2
1
C
Vent ,rms
R2
2
2
V0
2
2
X C2
2
1
C2
I1
6
0.4
120
I1
0.02 A
V2
I2
V1
 Exemplo 25 – Uma linha de transmissão tem
uma resistência de 0.02 /km. Calcule a perda de
energia se uma potência de 200 kW for transmitida de
uma usina geradora para uma cidade situada a 10 km de
39
distância
(a) com uma tensão de 240V;
(b) com uma tensão de 4.4 kV.

V0
2
2
C R2 1
2
C2
V0
2
2
C R2 1
C
1
C 2 R2 1
I1
Solução:
(a)
I
P
200kW
I
I 833A
V
240V
P R I2
P 0.2 8332
P 139kW
(b)
I
P
200kW
I
I 45.5 A
V
4.4kV
P R I2
P 0.2 45.52
P 414W
Observação: é vantajoso transportar a alta
tensão.
Observação: Esse circuito é denominado de filtro
RC passa baixas.
 Exemplo 24 – Uma campainha de porta funciona
com 6V e consome corrente de 0.4A. A campainha é
alimentada por um transformador cujo rolamento está
ligado a uma rede elétrica de 120V AC.
(a) Quantas espiras tem o rolamento secundário do
transformador?
(b) Qual é a corrente no circuito primário?

Solução
n
N2
N1
20
N2
N1
N2
V2
V1
6
1
120 20
2000
N2 100
20
39