Guião completo do 3º trabalho laboratorial

FEUP/DEEC/MIEEC - Laboratório de Sistemas Digitais 2006/07
Laboratório 3
LSDI 2006/07 - Laboratório 3: Construção de uma Unidade Lógica e Aritmética
1 - Introdução
Neste trabalho laboratorial será construído e ensaiado um circuito designado por Unidade Lógica e Aritmética (ou
ALU de Arithmetic Logic Unit). Este circuito é um componente importante de um microprocessador, responsável
pela realização das operações aritméticas e lógicas. O sistema digital que foi ensaiado no primeiro trabalho
laboratorial incluía uma unidade deste tipo que apenas suportava as operações de adição e subtracção,
semelhante ao que foi desenvolvido no laboratório 2 (addsub4).
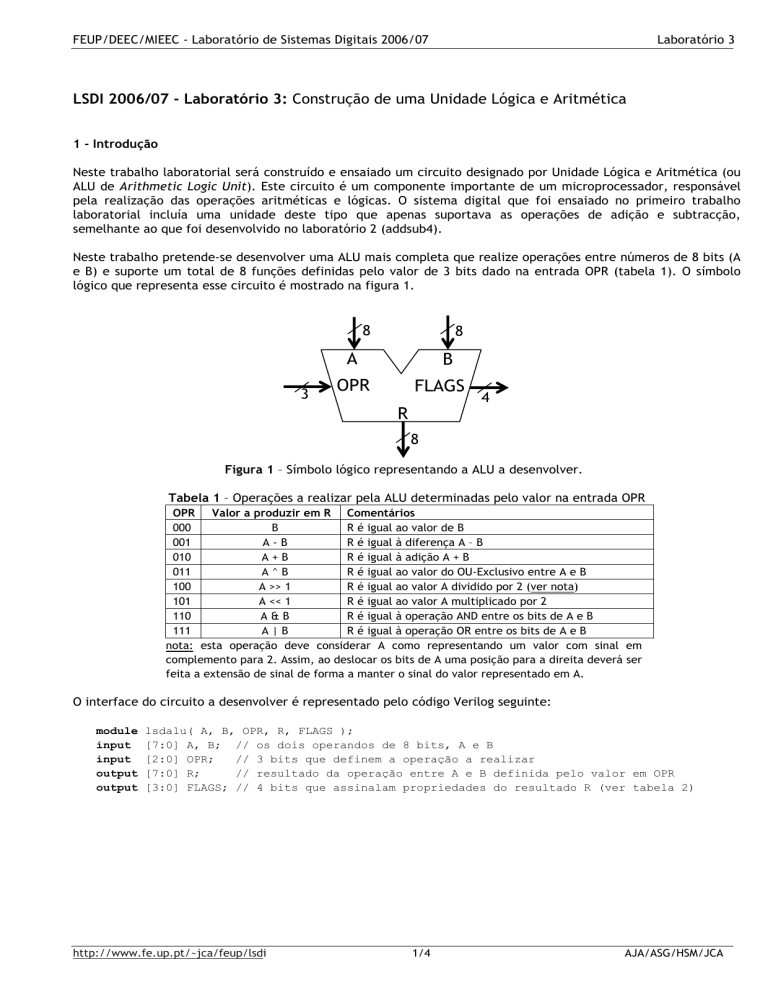
Neste trabalho pretende-se desenvolver uma ALU mais completa que realize operações entre números de 8 bits (A
e B) e suporte um total de 8 funções definidas pelo valor de 3 bits dado na entrada OPR (tabela 1). O símbolo
lógico que representa esse circuito é mostrado na figura 1.
8
8
A
3
B
OPR
FLAGS
4
R
8
Figura 1 – Símbolo lógico representando a ALU a desenvolver.
Tabela 1 – Operações a realizar pela ALU determinadas pelo valor na entrada OPR
OPR Valor a produzir em R Comentários
000
B
R é igual ao valor de B
001
A-B
R é igual à diferença A – B
010
A+B
R é igual à adição A + B
011
A^B
R é igual ao valor do OU-Exclusivo entre A e B
100
A >> 1
R é igual ao valor A dividido por 2 (ver nota)
101
A << 1
R é igual ao valor A multiplicado por 2
110
A&B
R é igual à operação AND entre os bits de A e B
111
A|B
R é igual à operação OR entre os bits de A e B
nota: esta operação deve considerar A como representando um valor com sinal em
complemento para 2. Assim, ao deslocar os bits de A uma posição para a direita deverá ser
feita a extensão de sinal de forma a manter o sinal do valor representado em A.
O interface do circuito a desenvolver é representado pelo código Verilog seguinte:
module
input
input
output
output
lsdalu( A, B, OPR, R, FLAGS );
[7:0] A, B; // os dois operandos de 8 bits, A e B
[2:0] OPR;
// 3 bits que definem a operação a realizar
[7:0] R;
// resultado da operação entre A e B definida pelo valor em OPR
[3:0] FLAGS; // 4 bits que assinalam propriedades do resultado R (ver tabela 2)
http://www.fe.up.pt/~jca/feup/lsdi
1/4
AJA/ASG/HSM/JCA
FEUP/DEEC/MIEEC - Laboratório de Sistemas Digitais 2006/07
Laboratório 3
Tabela 2 – Significado dos 4 bits da saída FLAG; nos casos contrários aos indicados o
bit correspondente deverá ser igual a zero.
bit da saída FLAGS
Comentários
FLAGS[0]
flag ZERO: é igual a 1 se o resultado R for igual a zero
FLAGS[1]
flag SINAL: é igual a 1 se R for negativo (bit de sinal igual a 1)
FLAGS[2]
flag CARRY: é igual a 1 se ocorrer carry na adição ou subtracção
FLAGS[3]
flag OVFL: é igual a 1 se ocorrer overflow na adição ou subtracção
nota: “flag” é uma designação corrente atribuída a um bit num sistema digital que serve para
assinalar o estado verdadeiro ou falso de uma condição associada ao resultado de uma
operação aritmética ou lógica
Este trabalho é composto por duas partes: projecto, a realizar em casa e entregar ao docente no início da aula
laboratorial, e a implementação e ensaio que será realizada na aula de laboratório. O trabalho de preparação em
casa consiste no desenvolvimento do módulo referido, que poderá ser complementado com a sua simulação caso
tenha acesso a um simulador de Verilog (por exemplo o ModelSim). Para isso é fornecido como anexo a este guião
um modelo de teste que o permite simular, verificando o seu funcionamento para algumas operações (ficheiro
lsdalu_testbench.v).
2 - Projecto
Uma forma de implementar o circuito pretendido consiste em construir diferentes circuitos combinacionais (com
declarações assign) que representem cada uma das operações realizadas, e depois numa declaração always @*
usar uma só instrução case...endcase que represente um multiplexer para escolher para a saída R o resultado
adequado em função do valor dado na entrada OPR. Por sua vez, cada um dos bits da saída FLAGS pode também
ser definido como circuitos combinacionais à custa de outras declarações assign ou always @*. Pode ser
seguido como exemplo o circuito somador-subtractor que foi apresentado na aula teórica no slide 58, que tem
uma funcionalidade parecida com a da ALU a desenvolver embora só faça 2 operações, adição e subtracção.
a) Considerando o interface referido acima, escreva as 8 declarações assign que implementam cada uma das
funções referidas na tabela 1. “Ligue” ao resultado de cada operação um wire de 8 bits com o nome ROPR0,
ROPR1,...,ROPR7, respectivamente para a operação efectuada quando OPR é igual a 0, 1,...,7
b) Escreva as 4 declarações assign (ou always @*) que definem os valores para os 4 bits da saída FLAGS. Note
que FLAGS[3] se refere ao bit 3 (o mais significativo) do sinal FLAGS e FLAGS[0] é o bit menos significativo.
Note que se utilizar declarações always @* os sinais a quem são atribuídos valores devem ser declarados
como sinais do tipo reg.
c) Escreva agora a declaração always @* que representa o multiplexer de 8 entradas que escolhe para a saída
R o sinal que representa o resultado de cada uma das declarações assign que foram construídas em a)
3 – Simulação do circuito
Após projectar o circuito lsdalu, simule-o usando para modelo de teste o que é dado no ficheiro anexo
lsdalu_testbench.v. Note que o circuito que pretende simular tem um total de 19 entradas (3+8+8) e 12 (4+8)
saídas e por isso uma simulação exaustiva (i.e. aplicando nas entradas todos os valores possíveis) obrigaria a testar
todas as 219=524288 situações diferentes. O modelo de teste não faz esta verificação exaustiva e aplica apenas
alguns valores em A e B para cada uma das operações (OPR), imprimindo o valor do resultado na janela de texto
do simulador.
a) Analise o código Verilog contido na declaração initial do modelo de teste e acrescente mais valores de
teste que lhe permitam verificar o correcto funcionamento das partes do seu circuito que produzem os valores
para a saída FLAGS.
b) Simule o seu circuito usando o módulo de teste dado e verifique que funciona conforme o esperado.
http://www.fe.up.pt/~jca/feup/lsdi
2/4
AJA/ASG/HSM/JCA
FEUP/DEEC/MIEEC - Laboratório de Sistemas Digitais 2006/07
Laboratório 3
4 – Implementação e ensaio
~
4.1 – Projecto ISE
Para ensaiar a unidade lógica e aritmética desenvolvida esta será integrada num projecto do programa ISE para a
placa S3BOARD, que implementa uma unidade de cálculo elementar. O circuito lógico que está construído neste
projecto é ilustrado na figura 2 onde se mostra a ligação das entradas e saídas aos botões de pressão,
interruptores, LEDs e mostradores.
Liga aos 8 interruptores
(sw7,sw6,…sw0)
8
Liga ao botão btn3
clock
pressionar o botão provoca
uma transição 0->1 de clock
Liga aos 3 botões
(btn2,btn1,btn0)
Liga aos 2 mostradores
da direita
A
8
A
3
OPR
Liga aos 2 mostradores
da esquerda
B
FLAGS
4
R
8
FLAGS
Liga aos 4 LEDs
(ld3, ld2, ld1, ld0)
Figura 2 – Circuito lógico implementado no projecto fornecido.
As entradas e saídas do circuito dado são as seguintes:
Os 8 interruptores de 2 posições (sob os mostradores) permitem definir, em binário, o valor do operando B da
ALU: colocando um interruptor para cima define um 1 e para baixo representa um zero. O valor colocado nestes
interruptores é afixado nos 2 mostradores da direita em hexadecimal.
O valor da entrada OPR da ALU é definido com os 3 botões de pressão do lado direito (btn2, btn1, btn0):
pressionando um botão coloca o bit correspondente igual a 1 (por exemplo, para definir a operação OU-Exclusivo
deve ser aplicada na entrada OPR o valor 011 o que é feito pressionando os botões btn1 e btn0).
A e FLAGS são registos (conjuntos de flip-flops do tipo D) que são actualizados sempre que o sinal clock passa de
0 para 1; esta acção é realizada pressionando o botão de pressão btn3 (botão mais à esquerda), o que faz carregar
o registo A com o resultado corrente na saída R da ALU e o registo FLAGS com o valor que a ALU produz na saída
FLAGS. O valor presente no registo A é afixado nos 2 mostradores do lado esquerdo e o estado das 4 flags é
mostrado no 4 LEDs (ld3, ld2, ld1, ld0).
4.2 – Implementação do projecto
Para implementar o projecto dado com a sua ALU basta abrir o projecto lsdi-lab3 no programa ISE, editar o
ficheiro lsdalu.v e incluir o código Verilog do modelo que construiu para a sua ALU. Note que deve respeitar
rigorosamente o interface dado na parte 1 do guião, nomeadamente no que se refere aos nomes dos sinais de
interface e ao nome do módulo, caso contrário a implementação não será realizada com sucesso.
Seleccionando o módulo lsdi-lab3, active a opção “Generate Programming File” ou então “Configure Device”; caso
não ocorram erros na implementação, programe a FPGA da placa e experimente o seu circuito.
4.3 - Como utilizar o circuito?
O circuito permite efectuar operações elementares entre um número de 8 bits e o valor presente no registo A.
Para realizar uma operação basta definir o valor do operando B actuando nos 8 interruptores, pressionar os botões
que definem a operação a realizar e (mantendo estes premidos) pressionar e largar o botão btn3 (o que provoca
http://www.fe.up.pt/~jca/feup/lsdi
3/4
AJA/ASG/HSM/JCA
FEUP/DEEC/MIEEC - Laboratório de Sistemas Digitais 2006/07
Laboratório 3
uma transição de 0 para 1 do sinal clock). O resultado produzido pela ALU é carregado no registo A e mostrado
em hexadecimal nos 2 mostradores da esquerda.
Por exemplo, para efectuar a adição 5 + 23 devem ser efectuados os seguintes passos:
1 - carregar o valor 5 para o registo A: colocar os interruptores com 00000101, não pressionar nenhum
dos botões que definem OPR (ou seja, OPR=000 o que coloca na saída da ALU o valor de B) e actuar
a entrada clock para carregar o registo A com o valor presente na saída da ALU que é o valor de B
2 – adicionar 23 ao valor de A e colocar o resultado no registo A: colocar os interruptores com 00010111
(B=23), colocar OPR=010 e actuar a entrada clock.
Combinando várias destas operações simples é possível efectuar cálculos com alguma complexidade, embora
restritos apenas a valores numéricos representados com 8 bits. Cada operação elementar, como as referidas no
exemplo acima, pode ser representada com uma notação simbólica que torna mais fácil especificar uma sequência
de operações necessárias para efectuar um determinado cálculo (tabela 3).
Tabela 3 – Operações elementares realizadas pelo circuito dado e representação simbólica de cada uma
OPR
000
001
010
011
100
101
110
111
Valor colocado no registo A
B
A-B
A+B
A^B
A >> 1
A << 1
A&B
A|B
operação simbólica
A←B
A←A-B
A←A+B
A←A^B
A ← A >> 1
A ← A << 1
A←A&B
A←A|B
Comentários
A fica como valor de B
A fica com o resultado de A - B
A fica com o resultado de A - B
A fica com o resultado do XOR entre A e B (A ^ B)
A fica com o valor de A deslocado para a direita 1 bit
A fica com o valor de A deslocado para a esquerda 1 bit
A fica com o resultado do E entre A e B (A & B)
A fica com o resultado do OU entre A e B (A | B)
Por exemplo, para calcular o valor da expressão ( ( (23-56) / 2 ) + 34 ) * 2 podemos escrever uma lista de 5
operações simbólicas que podem depois ser executadas na nossa calculadora, uma em cada transição do sinal
clock:
Operação simbólica
Como realizar
A
A
A
A
A
←
←
←
←
←
23
A – 56
A >> 1
A + 34
A << 1
Colocar
Colocar
Colocar
Colocar
Colocar
B com 23 e OPR com 000
B com 56 e OPR com 001
OPR com 100 (o valor de B não interessa)
B com 34 e OPR com 010
OPR com 101 (o valor de B não interessa)
4.4 – Ensaio do circuito
a) Defina um conjunto de dados e de operações que lhe permitam verificar todas as operações que a ALU
consegue realizar, verificando o valor das saídas FLAGS para cada caso.
b) Construa conjuntos de operações elementares, usando a notação simbólica introduzida acima, que permitam
calcular as expressões aritméticas seguintes:
4+4+5+6
-89 – ( 9 * 4 ) - 45
( 13 * 9 ) / 2
–3 * ( 15 + 8 ) - 99
127 + (- 128)
c) Experimente executar as sequências de operações elementares que construiu na alínea anterior e confirme os
resultados obtidos.
http://www.fe.up.pt/~jca/feup/lsdi
4/4
AJA/ASG/HSM/JCA