Guia do Professor
Matemática e Saúde
Experimentos
Coordenação Geral
Elizabete dos Santos
Autores
Bárbara N. Palharini Alvim Sousa
Karina Pessoa da Silva
Lourdes Maria Werle de Almeida
Luciana Gastaldi S. Souza
Márcia da Costa Trindade Cyrino e
Rodolfo Eduardo Vertuan
Revisão Textual
Elizabeth Sanfelice
Coordenação de Produção
Eziquiel Menta
Projeto Gráfico
Juliana Gomes de Souza Dias
Diagramação e Capa
Aline Sentone
Juliana Gomes de Souza Dias
Realização
Secretaria de Estado
da Educação do Paraná
DISTRIBUIÇÃO GRATUITA
IMPRESSO NO BRASIL
2
Experimento de Ensino
Matemática e Saúde
1 Introdução
O experimento de ensino “Matemática e Saúde” tem como objetivo discutir conceitos
da estatística descritiva, mais especificamente, medidas de tendência central e medidas
de dispersão, a partir de um tema da atualidade – a Gripe Suína. É intenção do experimento que os alunos aprendam a construir tabelas de frequências, bem como conceitos
de média, moda, mediana e desvio padrão, por meio do estudo da abordagem realizada
na situação. Para que os alunos apliquem os conceitos estudados, em exercícios de sala
de aula ou extraclasse, propõe-se uma situação real, ligada à saúde: o caso da dengue.
Trata-se de mais um recurso que, aliado ao audiovisual “Endireitando a Coluna”, possibilita aos alunos aplicarem conhecimentos já construídos bem como revisarem conceitos e
procedimentos presentes em situações do cotidiano – situações relacionadas à estatística,
tal qual a analisada no experimento –, com a incidência de Síndrome Respiratória Aguda
Grave por Influenza A (H1N1).
1.1 Gripe Suína
Em meados de março de 2009, a população mundial foi surpreendida com uma nova
variação do vírus da gripe suína, nunca antes visto ou identificado. Embora tenha surgido
no México, não demorou muito para que o vírus se espalhasse por várias partes do mundo, dentre elas o Brasil. Ele foi identificado como uma nova ramificação do já conhecido
Influenza A subtipo H1N1, o mesmo vírus responsável pelo maior número de casos de
gripe entre humanos, o que tornou possível a designação nova gripe A, em oposição à
gripe A comum.
Nos adultos, os sintomas mais comuns da gripe H1N1 são muito semelhantes aos da
gripe comum. Eles incluem a falta de apetite, tosse, falta de energia e febre. Outros sintomas podem incluir náuseas, diarréia, vomito, dor de garganta e, eventualmente, uma
coriza nasal. Em crianças, são sintomas, ainda, a irritabilidade, a alteração na cor da pele,
a falta de vontade de beber líquidos e os problemas respiratórios, como respiração acelerada ou respirações curtas.
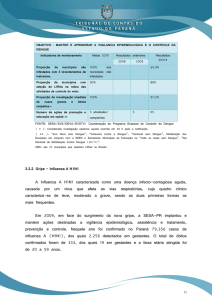
Segundo o protocolo de vigilância da Influenza, são considerados casos de síndrome
respiratória aguda grave (SRAG) aquelas pessoas que apresentam febre, tosse e dispnéia.
No gráfico abaixo, é possível perceber o número de casos de SRAG, no Brasil, até 18 de
julho de 2009, data referente à semana epidemiológica (SE) 28.
Figura 1:
Distribuição de casos de SRAG
(Síndrome Respiratória Aguda
Grave) por semana epidemiológica. Brasil, até semana
epidemiológica 28 de 2009.
Captura em 22 de março de
2010: <http://portal.saude.
gov.br/portal/arquivos/pdf/
boletim_epidemiologico_influenza_23_07_2009.pdf>
3
No quadro que segue estão as informações sobre o número de casos confirmados de
SRAG por Influenza A (H1N1), no Brasil, segundo faixa etária.
Figura 2:
Distribuição de casos confirmados de SRAG (Síndrome
Respiratória Aguda Grave)
por Influenza A (H1N1),
segundo classificação etiológica e faixa etária. Brasil, até
semana epidemiológica 28
de 2009. Captura em 22 de
março de 2010: <http://portal.
saude.gov.br/portal/arquivos/
pdf/boletim_epidemiologico_
influenza_23_07_2009.pdf>.
Em março de 2010, cerca de um ano após o início da epidemia, o Brasil iniciou a vacinação da população. A expectativa do Ministério da Saúde era de vacinar cerca de 90
milhões de pessoas em dois meses. Mas para isso foi preciso organizar um calendário em
que diferentes grupos pudessem ser vacinados, cada um a seu tempo. A definição destes
grupos considerou o histórico da gripe H1N1 mundial. Dentre os fatores considerados,
está a idade das pessoas (Conheça o calendário da gripe H1N1 na página <http://www.
gripesuinah1n1.com/calendario-vacinacao-da-gripe-suina-h1n1-no-brasil.html>).
1.2 Estatística
Estatística é a ciência que se ocupa da recolha e tratamento de informação. Tem como
objetivo analisar os dados recolhidos, descrevendo-os e organizando-os para posterior
interpretação e eventual utilização na previsão de acontecimentos futuros.
A Estatística divide-se em dois ramos distintos: a Estatística Descritiva, responsável pelo
estudo das características de uma dada população; e a Estatística Indutiva, que generaliza um conjunto de resultados, tendo por base uma amostra de uma dada população ou
universo, enunciando a consequente lei.
1.2.1 Tabelas de Frequências
As tabelas de frequências ou distribuições de frequências resumem a informação contida numa amostra, ordenando os seus valores e agrupando-os em classes de valores repetidos ou de valores distribuídos por intervalos.
Na tabulação dos dados, fazemos uma lista de todos os valores de um atributo e à frente de cada um colocamos o número de vezes que esse atributo ou valor ocorreu. Esta é a
tabela de frequências absolutas. A frequência absoluta (FA), ou apenas frequência de um
valor, é o número de vezes que uma determinada variável assume esse valor.
Existem, ainda, as frequências relativa (FR), absoluta acumulada (FAA) e relativa acumulada (FRA).
A frequência relativa é a porcentagem relativa à frequência absoluta, a frequência
acumulada de um valor é o numero de vezes que uma variável assume um valor inferior
ou igual a esse valor e, finalmente, a frequência relativa acumulada é a porcentagem
relativa à frequência acumulada.
Podem calcular-se frequências absolutas e relativas de todas as variáveis, sejam elas
qualitativas ou quantitativas. Variáveis quantitativas são aquelas numericamente mensuráveis e as qualitativas são aquelas que se baseiam em qualidades e não podem ser
mensuráveis.
4
As variáveis quantitativas podem ser variáveis discretas (obtidas por contagem), como
acontece na situação por ora estudada, em que a variável em questão é a idade da pessoa que adquiriu SRAG por influenza A. Considera-se, neste caso, as idades completas das
pessoas, as quais são representadas por números inteiros positivos. Já as variáveis contínuas
(obtidas por medida) podem ser exemplificadas com a altura ou com a massa de um indivíduo.
1.2.2 Medidas de Tendência Central
São medidas de localização dentro de uma distribuição de dados: a média aritmética,
x=
x1 + x2 + x3 + ... + xn
n
a moda e a mediana.
Dados n valores x1, x2, x3, ..., xn, chama-se média aritmética (x-) destes n valores, ao valor
A moda é o valor mais frequente na distribuição. Para encontrar o valor da moda quando os dados não estão agrupados ou quando estão agrupados em uma distribuição de
frequências por valores simples, basta identificar o valor que mais aparece no conjunto de
informações. Quando os dados estão agrupados em uma distribuição de freqüências por
Mo = i +
∆1
.h
∆1 + ∆ 2
classes, podemos utilizar, para o cálculo da moda, a seguinte fórmula, conhecida como
fórmula de Czuber.
em que:
li é o limite inferior da classe modal
∆1 é a diferença entre a frequência simples da classe modal e da classe anterior à modal
∆2 é a diferença entre a frequência simples da classe modal e da classe posterior à modal
h é a amplitude da classe modal
A mediana é o elemento que ocupa a posição central da distribuição, deixando 50%
dos demais valores antes dele e 50% depois. Assim como no caso do cálculo para a moda,
para calcular a mediana quando os dados não estão agrupados ou quando estão agrupados em uma distribuição de frequências por valores simples, basta identificar o valor que
ocupa a posição central no conjunto de informações. Quando os dados estão agrupados
n
− Fac ,ant
2
.h
Md = li +
Fi
em uma distribuição de frequências por classes, podemos utilizar, para o cálculo da mediana, a seguinte relação.
5
em que:
li é o limite inferior da classe mediana
n é o número de elementos da amostra
Fi é a frequência simples da classe mediana
Fac,ant é a frequência acumulada da classe imediatamente anterior à classe mediana
h é a amplitude da classe mediana
1.2.3 Medidas de Dispersão
Para investigar a variabilidade dos dados em torno da média, utilizamos algumas medidas de dispersão. As medidas de dispersão indicam se os valores estão próximos uns dos
outros, ou separados, em torno de uma medida de posição: a média. Nesta investigação,
trataremos do desvio médio, da variância e do desvio padrão.
O desvio médio analisa a média dos desvios em torno do valor médio. Para seu cálculo,
n
DM =
∑ x − x .F
i
i =l
i
n
utilizamos, quando os dados estão agrupados em uma distribuição de frequências por
classe, como na situação, a seguinte relação:
sendo n o total de casos (220 na situação), Fi a frequência de cada intervalo, xi a média
aritmética entre os extremos de cada intervalo e a média do conjunto de dados.
A variância de um conjunto de dados é a média dos quadrados dos desvios dos valores
a contar da média. À raiz quadrada da variância, denomina-se desvio padrão. Para uma
n
2
S =
∑( x − x )
i =l
i
n−l
2
.Fi
e DP = S 2 = S
amostra cujos dados são agrupados em uma distribuição de freqüências por classes, utilizamos a relação para o cálculo da variância (S2) e desvio padrão (DP):
2 Objetivos
Espera-se, com este experimento de ensino, que os alunos:
• conheçam algumas medidas de tendência central (moda, mediana e média aritmética)
e medidas de dispersão (desvio médio, variância e desvio padrão);
• identifiquem o uso de conceitos da estatística – tendência central e variabilidade –
para analisar situações;
• apliquem os conceitos de medidas de tendência central e variabilidade em situações
reais.
3 Tempo previsto para a atividade
O tempo previsto para a atividade é de aproximadamente uma hora e meia. No entanto, esse tempo pode variar de acordo com o potencial de intervenção do professor
antes da execução da atividade ou mesmo durante sua execução. Recomenda-se que
6
o professor aproveite a oportunidade dos momentos no ambiente laboratorial para
explorar cada conceito matemático presente no experimento. Tais discussões pormenorizadas tendem a potencializar a aprendizagem dos alunos bem como possibilitar a
investigação das situações que seguem, tal como a “incidência de dengue na população
de uma cidade de acordo com a faixa etária”.
4 Na sala de aula
Aliado ao experimento de ensino o professor pode utilizar o audiovisual “Endireitando a Coluna”, que trata dos mesmos conceitos matemáticos. Se apresentado antes deste
experimento de ensino, o áudio visual pode ser utilizado como um convite aos alunos
para investigarem os conceitos deste ramo da Matemática. Os alunos podem, inclusive,
discutir temas para futura investigação.
Considera-se importante, ainda, que o professor utilize o simulador e explore suas
possibilidades antes de submetê-los aos alunos, de modo a potencializar sua intervenção
no decorrer das atividades.
5 Sugestão de atividade
A fim de complementar o presente experimento de ensino e de levar os alunos a utilizarem as medidas de tendência central e de variabilidade para analisar situações do cotidiano,
o professor pode pedir que eles realizem uma pesquisa, em grupos, com um tema de seu
interesse. Podem investigar com os demais alunos da escola, os quais serão considerados
uma amostra representativa do universo (todos os alunos), sua opinião em relação a assuntos diversos. Neste contexto, como realizar uma pesquisa estatística, quais variáveis estão
envolvidas na pesquisa, que público pesquisar para que a pesquisa não seja tendenciosa e
como organizar os dados, serão alguns dos assuntos presentes nas discussões.
Como sequência natural do experimento de ensino, o professor deve propor que os
alunos investiguem a situação sobre a incidência de dengue na população de uma cidade
de acordo com a faixa etária. Segue a situação:
Realize um estudo estatístico da situação “Incidência de dengue na população de
uma cidade de acordo com a faixa etária”, construindo uma tabela de freqüências
e calculando as medidas de tendência central e as medidas de dispersão dos dados.
Analise a situação a partir dos resultados encontrados.
“Incidência de dengue na população de uma cidade de acordo com a faixa etária”
A dengue é uma doença infecciosa aguda de curta duração, de gravidade variável,
causada por um arbovírus, do gênero Flavivírus (sorotipos: 1,2,3 e 4). No Brasil, circulam os tipos 1, 2 e 3. O vírus 3 está presente desde dezembro de 2000 e foi isolado em janeiro de 2001, no Rio de Janeiro. A dengue é transmitida principalmente
pelo mosquito Aedes aegypti infectado, mas também pode ser transmitida pelo
Aedes albopictus. Esses mosquitos picam durante o dia, ao contrário do mosquito
comum (Culex), que pica durante a noite.
O Aedes aegypti é principalmente encontrado em áreas tropicais e subtropicais do
mundo, inclusive no Brasil, pois as condições do meio ambiente favorecem o seu
desenvolvimento e sua proliferação. As epidemias geralmente ocorrem no verão,
durante ou imediatamente após períodos chuvosos.
Para a próxima atividade, será utilizada a tabela da figura 3, que relaciona a faixa
etária de uma pessoa com a taxa de incidência da dengue em homens e mulheres
para o ano de 2001 e 2002 na cidade de São Sebastião, SP.
7
Figura 3:
Taxa de incidência de dengue
segundo sexo e faixa etária. São Sebastião – SP. 2001
e 2002. Captura em 22 de
março de 2010: <http://www.
dengue.lcc.ufmg.br/dengue_
cd/files/epidemiologia/textos/
associacaodengueevariaveisclimaticas.pdf>.
Deste conjunto de informações, investigue:
• a idade média em que as pessoas tiveram maior incidência de dengue nos anos de
2001 e 2002 em São Sebastião – SP. Obs: desconsidere o sexo das vítimas. Considere os
1691 casos referentes à soma dos infectados de 2001 e 2002, e construa uma tabela de
freqüências para organizar as informações;
• a variabilidade em torno da idade média.
6 Avaliação
A avaliação pode ser realizada durante todo o desenvolvimento das atividades, por
meio de questionamentos. O professor pode aproveitar as respostas dos alunos para fazer as intervenções que julgar necessárias.
8
Condigital
Realização: