Nu - Tolstenko

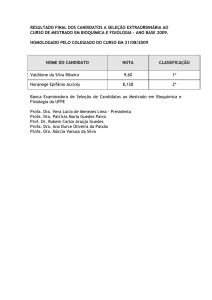
Capítulo 6: Escoamento Externo
Hidrodinâmica
Conceitos fundamentais
Arrasto total
Transferência de calor
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Fluido
• É qualquer substância que se deforma
continuamente quando submetido a uma
tensão de cisalhamento, ou seja, ele escoa.
• Fluidos existem como líquido (água,
gasolina), gás (ar, hidrogênio) e como uma
combinação de líquido e gás (vapor úmido).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Propriedades de um fluido
• São várias as propriedades que permitem
distinguir os fluidos e que são independentes
do seu movimento:
– Densidade;
– Pressão de vapor;
– Tensão superficial (atração molecular de um
líquido próximo de uma superfície ou outro fluido);
– Velocidade do som (velocidade na qual a onda
acústica se movimenta no fluido).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Fluidos incompressíveis x compressíveis
• Fluidos compressíveis
– São aqueles que apresentam variação na
densidade quando escoam: usualmente os
gases.
• Fluidos incompressíveis
– São aqueles que não apresentam variação da
densidade quando escoam (densidade constante
ao longo do escoamento): usualmente líquidos e
alguns gases.
• Neste curso serão considerados apenas os
fluidos incompressíveis (ideais).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Escoamento incompressível x
compressível
• A diferença entre o escoamento incompressível e
compressível pode ser verificado através do
número de Mach:
V
M=
c
• Onde V é a velocidade do fluido e c é a velocidade
do som.
• Esta equação permite determinar qual o
escoamento de um fluido.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Movimento de um fluido
Pode ser analisado segundo duas descrições:
• Lagrangiana: é a descrição de movimento na qual as
partículas individuais são observadas em função do
tempo.
– Torna-se uma tarefa bastante difícil quando o número de
partículas é muito grande, como no escoamento de um
fluido.
• Euleriana: é a descrição de movimento na qual as
propriedades de escoamento (como a velocidade) são
funções do espaço e do tempo.
– A região de escoamento considerada é o campo de
escoamento.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Campo de escoamento
Linhas de corrente: definidas como a linha contínua
que é tangente aos vetores velocidade ao longo do
escoamento num dado instante t.
As linhas de corrente são sempre paralelas ao
escoamento.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Escoamento externo X interno
• Escoamento externo é aquele que ocorre
externamente a uma superfície sólida, onde o fluido
está em contato com uma única fronteira sólida;
• Escoamento interno é aquele que possui fronteiras
limitando o campo de escoamento:
– No escoamento interno, os efeitos viscosos causam perdas
energéticas substanciais e são responsáveis por grande
parte da energia necessária para transportar óleo e gás em
tubulações.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Força externa total no VC
A força externa total atuando em um VC é:
∑F
VC
∑F
VC
= F grav + Fpres + Fvis
= ρgV + ∫∫ (-n) P dA + ∫∫τ dA
SC
EM-524 Fenômenos de Transporte
SC
Profa. Dra. Carla K. N. Cavaliero
Tensão de cisalhamento
Ao encontrar uma fronteira sólida, o fluido se
deforma devido à aplicação de forças de
cisalhamento (que agem paralelamente às
superfícies do fluido).
Enquanto esta força estiver atuando, o fluido
continuará se deformando.
Esta força é resultado de uma tensão (de
cisalhamento) agindo sobre o fluido, que exerce
uma oposição ao movimento do fluido.
Energia deve ser fornecida para vencer esta
resistência e manter o escoamento.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Tensão de cisalhamento
• Existem fluidos em que a relação entre a tensão
de cisalhamento e a taxa de deformação é linear e
pode ser expressa por:
Taxa de deformação
∂u
τx = µ
∂y
Viscosidade dinâmica
É uma propriedade intensiva,
também conhecida como
viscosidade absoluta (SI : N.s/m2)
Apresenta valores tabelados
variando com T e P.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Gradiente de velocidade
• Devido o princípio da aderência o fluido
em contato com uma superfície sólida
possui a velocidade da superfície.
• Na medida em que afasta da parede, a
velocidade do fluido relativa à parede
aumenta, variando desde a velocidade
da superfície (zero) até um valor máximo
finito (U).
• Essa variação de velocidade é chamado
de perfil de velocidade ou gradiente de
velocidade.
• A tensão de cisalhamento age no
sentido de resistir ao movimento do
fluido, sendo máxima na superfície onde
não existe movimento relativo.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Camada limite hidrodinâmica
• É uma camada
relativamente fina onde os
u = 0,99U em y = δ
efeitos das tensões
viscosas de cisalhamento
δ
são preponderantes
(escoamento viscoso),
u = 0 em y = 0
existindo o gradiente de
velocidade.
• A espessura da camada limite, δ, corresponde a distância a
partir da qual o valor da velocidade do fluido corresponde a
uma fração da velocidade a montante U.
• Logo:
u = 0 em y = 0
u = 0,99 U em y = δ
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Sem Viscosidade
Com Viscosidade
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Escoamento na camada limite
• Experimentos mostram que existem dois regimes de
escoamento na camada limite: laminar e turbulento.
• Escoamento laminar: fortemente ordenado
– As partículas mantém seu padrão de comportamento;
– O mecanismo de difusão é somente o molecular;
– O escoamento se processa na forma de “lâminas”
sobrepostas.
• Escoamento turbulento: fortemente desordenado
– As partículas não apresentam um padrão de comportamento;
– O mecanismo de difusão não é somente o molecular;
– Ocorre difusão devido ao movimento desordenado das
partículas – choques.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Escoamento na camada limite
• Os regimes de escoamento laminar e turbulento
podem ser caracterizados considerando-se a
relação entre a força de inércia numa partícula
fluida e a força viscosa agindo nessa partícula
fluida.
• Essa relação é adimensional e é conhecida como
Número de Reynolds (Re).
ρL3 U 2
força inercial M.a
ρUL UL
L
Re =
=
=
=
=
U
força viscosa τ.A µ L2
µ
ν
L
EM-524 Fenômenos de Transporte
ρUL UL
Re =
=
µ
ν
Profa. Dra. Carla K. N. Cavaliero
Recr em placas planas
• Existe um valor crítico de Re acima do qual o
escoamento será turbulento e abaixo do qual será
laminar.
• Este valor é conhecido como número de Reynolds
de transição ou crítico.
• Experimentos realizados em uma placa plana lisa
indicaram que o valor crítico de Re, baseado na
distância ao longo da placa (a contar da borda do
ataque) é aproximadamente 5 x 105.
• Caso a superfície da placa seja rugosa, o valor de
Recr estará no intervalo 8 x 103 – 5 x 105.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Escoamento em regime permanente X
transiente
• No escoamento em regime permanente não há
alteração das propriedades da partícula ao longo
do tempo.
– Logo, as quantidades de interesse no escoamento de
um fluido (como por exemplo velocidade, pressão e
densidade) são independentes do tempo.
• No escoamento em regime transiente as
propriedades da partícula se alteram ao longo do
tempo.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Capítulo 6: Escoamento Externo
Hidrodinâmica
Arrasto viscoso e de pressão
Arrasto total
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Escoamento externo
A medida que um fluido escoa ao passar por uma placa plana,
o atrito exerce seu efeito de duas maneiras:
• Uma é a aplicação direta de uma força de atrito (viscosa)
causada pela tensão de cisalhamento atuando sobre esta
placa ⇒ associado ao chamado arrasto viscoso ou de atrito.
• A outra está relacionada ao fato de os efeitos do atrito no
fluido que escoa poderem alterar drasticamente o percurso
do fluido em torno da placa plana. Estes efeitos causam uma
queda de pressão irreversível na direção do escoamento (a
pressão na parte posterior da placa é menor que na parte
frontal) ⇒ associado ao arrasto de pressão ou de forma.
• O arrasto total sobre a fronteira do VC é a combinação do
arrasto de atrito com o de pressão.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto viscoso ou de atrito
• É o resultado do efeito da camada limite:
– É originário dos efeitos viscosos, associados à tensão de
cisalhamento, atuantes nas paredes sólidas.
• A tensão de cisalhamento age no sentido de resistir ao
movimento do fluido, ou seja, no sentido oposto a
deslocamento no eixo x, e quando multiplicada pela área
apropriada, resulta na força viscosa.
• Assim, esta força viscosa agirá SEMPRE no sentido de se
opor ao movimento
• Quando define-se o VC e a sua superfície coincide com a
superfície sólida, surge uma reação à esta tensão sobre esta
superfície sólida, na direção positiva do deslocamento no
eixo x, e oposta à direção da força viscosa sobre o fluido.
• Essa força de reação é chamada de força de arrasto viscosa.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto viscoso ou de atrito
• A tensão de cisalhamento é determinada pela viscosidade e
pelo gradiente de velocidades.
• Devido as dificuldades de se determinar o gradiente de
velocidades, pode-se determinar a tensão por meio do
coeficiente de atrito de Fanno (Cf):
Cf =
τp
(1/2)ρU ext
2
Onde τp é a tensão de
cisalhamento na parede do
objeto
• Existem Cf tabelados para alguns objetos e para a camada
limite laminar e a camada limite turbulenta.
• Muitas vezes, o Cf se obtém a partir da relação com o Re.
Tais relações são tabeladas para diversos tipos de objetos.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto viscoso ou de atrito
• A força de arrasto viscosa (Df) é determinada considerando
que a força de arrasto de pressão é nula.
• Logo, DF é obtida pela multiplicação da tensão pela área do
objeto:
2
DF = Cf (1/2)ρU ext A
• Existe uma expressão que permite determinar o arrasto de
atrito para uma placa plana lisa tanto para a camada limite
laminar quanto para a turbulenta. Esta expressão utiliza o
coeficiente médio de atrito:
2
DF = Cf (1/2)ρU ext A
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Coeficientes de arrasto de atrito
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto de Pressão
• Em grande parte das situações existe uma
gradiente de pressão na direção do escoamento do
fluido.
• Conhecendo-se a área, haverá uma força de arrasto
associado ao gradiente de pressão.
• O arrasto devido à pressão apresenta uma total
dependência do formato do corpo, sendo por isso
denominado também de arrasto de forma. Isso se
dá, porque seu valor é atribuído de acordo com as
distribuições de pressão ao longo da geometria
submetida ao escoamento.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto de Pressão
• O arrasto de pressão vai contribuir para a
resistência total sofrida pelo fluido e
resultará num fenômeno chamado de
separação do escoamento ou deslocamento
da camada limite.
• No descolamento existe um gradiente de
pressão entre a região frontal de estagnação
(alta pressão) e a região do descolamento
(baixa pressão).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Separação do escoamento
1 dP
dU
= −U
ρ dx
dx
• Nos bocais:
– A velocidade U do fluido está crescendo na direção do escoamento, dU/dx > 0;
– Isto significa que o gradiente de pressão na direção do escoamento é negativo,
dP/dx <0;
– Assim a força de pressão resultante no fluido age de forma favorável, na
direção do escoamento.
• Nos difusores:
A velocidade U está decrescendo na direção do escoamento, dU/dx < 0;
O gradiente de pressão é positivo, dP/dx > 0;
E a resultante força de pressão age retardando o escoamento.
Este gradiente de pressão é chamado de gradiente de pressão adverso. Isto
quer dizer que a quantidade de movimento do fluido está decrescendo e o
fluido próximo à superfície pode ser levado ao repouso numa distância
qualquer a partir da parede (u=0, y>0).
– Quando isto ocorre, o escoamento se separa.
–
–
–
–
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto total
• O arrasto total é soma do arrasto de atrito e de
pressão:
DT = DF + DP
• É determinado pelo coeficiente de arrasto, definido
por:
DT
CD =
2
U
ρ
A
2
• Este coeficiente apresenta-se definido para cada tipo
de objeto.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto de pressão
• É obtido por aproximação a partir do arrasto
total e do arrasto de atrito.
• O arrasto de atrito é calculado conhecendose a área da superfície do objeto e o número
de Reynolds do escoamento e considerando
o arrasto de pressão nulo.
• A diferença entre o arrasto total e o arrasto
de atrito fornece o arrasto de pressão.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Arrasto total em placas planas
• No caso do escoamento de um fluido ocorrer
paralelo ao comprimento de uma placa plana,
a contribuição do arrasto de pressão é nula
pois somente os efeitos viscosos
predominam. Logo, só há o arrasto de atrito.
• Quando o escoamento do fluido for normal à
placa plana, o arrasto por unidade de largura
refere-se apenas ao arrasto de pressão, pois
a tensão de cisalhamento será normal ao
escoamento. Logo não há arrasto de atrito.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Força de arrasto
• A redução da força de arrasto é muito importante
para o desenvolvimento de aviões, caminhões e
automóveis mais econômicos.
• O arrasto total multiplicado pela velocidade de
tráfego gera a potência necessária para vencer os
efeitos viscosos e de pressão e equivale a uma
parcela significativa da potência total que deve ser
produzida pelo motor do veículo.
• Por isto, várias pesquisas vêm sendo desenvolvidas
para determinar métodos de redução de arrasto
para diferentes objetos em movimento.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Capítulo 6: Escoamento Externo
Efeitos térmicos
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Transferência de Calor
• Condução
– É a energia que está sendo transferida através de uma
substância (sólido ou fluido) em função do gradiente de
temperatura dentro da própria substância.
• Convecção
– É a energia transferida entre um fluido e uma superfície
sólida em função do movimento do fluido. Pode ser:
• Natural e forçada.
• Radiação
– É a energia transferida por ondas eletromagnéticas.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Convecção forçada x natural
• Quando o movimento do fluido é gerado por
um dispositivo externo ao sistema, a
convecção é forçada.
• Caso contrário, é natural:
– Nesse caso, a transferência de calor em si
garante a fonte necessária para realizar o
movimento.
– Essa força surge devido às diferenças de
densidades quando se aquece o fluido.
– Normalmente não se verifica velocidade do
fluido.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Fluxo de Calor por Convecção
• Pode ser determinado por:
•
Q = h. A.(Tp − T∞ )
Calor total transferido em [W].
Onde h = coeficiente de transferência de calor por convecção;
Tp = temperatura da superfície;
T∞
∞ = temperatura do fluido fora da camada limite.
"
q& = h.(T p − T∞ )
Ou
Fluxo de calor por unidade de área [W/m2].
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
h médio
• Desta forma, é definido um valor médio para h
como:
L
∫ h dx
s
h=
0
L
EM-524 Fenômenos de Transporte
⇒ Q& = h . A.(T p − T∞ )
Profa. Dra. Carla K. N. Cavaliero
Camada limite térmica
• Caso a superfície sólida esteja a uma temperatura
diferente da corrente livre de escoamento (fora da
camada limite), uma camada limite térmica também
será formada.
• Sua taxa de desenvolvimento e espessura são
semelhantes aos da camada limite hidrodinâmica.
• A relação entre as camadas limite térmica e
hidrodinâmica é indicada pelo número de Prandtl:
ν cpµ
Pr = =
α
k
• Pr de vários fluidos está tabelado (Tabela A-8 e outras).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Camada limite térmica
N. Prandtl, Pr
ν δh
Pr = =
α δT
EM-524 Fenômenos de Transporte
Onde ν é a viscosidade cinemática e α é a
difusividade térmica.
O Pr pode ser interpretado como a
razão entre as espessuras das camadas
limites hidrodinâmica e térmica.
Profa. Dra. Carla K. N. Cavaliero
Camada limite térmica x hidrodinâmica
δh
(1 3 ) Regime
= 1,026 Pr
δT
Laminar
EM-524 Fenômenos de Transporte
Regime
δh
≅1
δT
Turbulento
Profa. Dra. Carla K. N. Cavaliero
Perfil de temperatura: aquecimento e
resfriamento do fluido
T∞
T∞
T∞
δT
Tp
Aquecimento
Tp > T∞
EM-524 Fenômenos de Transporte
Tp
Resfriamento
Tp < T∞
Profa. Dra. Carla K. N. Cavaliero
Número de Nusselt
• Da definição de h e de camada limite térmica, podese escrever que:
hx
hx x x
1
hx ≅
⇒ =
⇒
=
δT
k δT
k
δT
k
• Correlações para determinar o coef.
de transf. de calor por convecção
(h) são usualmente expressas em
termos do número de Nusselt local
ou médio.
EM-524 Fenômenos de Transporte
hx x
Nu x =
k
hL
Nu =
k
Profa. Dra. Carla K. N. Cavaliero
Número de Nusselt
hx x
Nu x =
≅ f ( Re, Pr )
k
• A forma exata da relação funcional vai depender da
configuração geométrica da superfície, da natureza
do escoamento e das condições de contorno
térmicas na superfície.
• As condições de contorno térmicas usuais são:
– Temperatura uniforme na superfície;
– Fluxo de calor uniforme.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Nu: Convecção Forçada
Temperatura da Parede Uniforme
Propriedades avaliadas em T∞
Rex < 5.103
Transição:
5.103 < Rex < 5.105
Nu =
5.105 < Rex <5.107
EM-524 Fenômenos de Transporte
Nu T2 + Nu L2
Expressão para
valor médio de
Nu é válida
somente se
0,5 < Pr < 2000
Profa. Dra. Carla K. N. Cavaliero
Nu: Convecção Forçada
Fluxo de Calor Uniforme
PLACA PLANA LISA
Laminar:
Turbulento:
1/ 2
Nu x = 0 , 46 (Re x )
Pr 1 / 3
0 ,8
0 , 0296 Re x Pr
Nu x =
− 0 ,1
1 + 2 ,185 Re x (Pr 2 / 3 − 1)
0 , 037 Re 0 , 8 Pr
N uT =
1 + 2 , 443 Re − 0 ,1 (Pr 2 / 3 − 1)
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Analogia entre atrito e calor
• Quando Pr = 1, as camadas limite térmica e
hidrodinâmica são idênticas, ou seja, existe uma
semelhança entre a quantidade de movimento e de
calor transferido.
• Pode haver uma relação simples entre o coef. de
arrasto de atrito e coef. médio de transferência de
calor em uma placa plana:
Cf
h
Nu
=
=
St =
2
ρc p U Re L Pr
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Analogia entre atrito e calor
• Para o intervalo 0,6 < Pr < 60:
Cf
23
= S t ⋅ Pr
2
• Chilton-Colburn – válida para: i) escoamento
laminar numa placa plana e ii) escoamentos
turbulentos sobre superfícies planas ou com
curvaturas.
• Útil para calcular coef. transferência de calor em
superfícies rugosas.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Convecção natural
Grx =
gβ (Tp − T∞ )x
ν
2
3
(número de Grashof)
Onde g = 9,08 m/s2
β = coeficiente de expansão volumétrica =
(para gás ideal β = 1/Tf onde Tf = (Tp+T∞)/2)
Ra x = Grx .Pr
(número de Rayleigh)
Para a placa plana vertical, a transição do
escoamento laminar para o turbulento ocorre a
Rax ≅ 109
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Nu: Convecção Natural
Placa Plana Isotérmica Vertical
Propriedades avaliadas em Tf
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Nu: Convecção Natural
Placa Plana Isotérmica Horizontal
Onde L = área/perímetro
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Correlações para cilindros e esferas
• 1< ReLc < 105 &
0,6 < Pr < 1000
Escoamento Forçado
Número de Nusselt médio para outros objetos de formas variadas com
temperatura de parede uniforme:
Nu = Nu 0 +
2
Nu lam
2
+ Nu tur
onde o comprimento característico Lc (Re e Nu) e Nu0 são dados na
tabela 6-5:
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Correlações para cilindros e esferas
• ReLc < 1 &
0,6 < Pr < 1000
Escoamento Forçado
Fio, cilindros e tubos:
Esferas:
Nu = 0,75(Re Lc Pr)1/ 3
1/ 3
Nu = 1,01(Re Lc Pr)
onde o comprimento característico Lc (Re e Nu) e Nu0 são dados na
tabela 6-5
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Correlação para cilindros e esferas –
convecção natural
• Correlação geral para cálculo do coef. transf. calor
em convecção natural para objetos de formas
variadas (válida para regiões laminar e turbulenta):
2
(
1
6
)


(1 2 )
( )
Nu =  Nu 0


ξ (Pr ) =
 Ra Lc ⋅ ξ (Pr ) 
+ 

300





1
(9
6)
(16
9)


 0 ,5 

1 + 

 Pr 


O comprimento característico LC (Ra e Nu) e Nu0 são dados na
Tabela 6-6.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Convecção Natural x Forçada
• Para cada situação haverá uma correlação
específica para Nu.
• Deve-se tomar cuidado ao se determinar os
parâmetros de referência pois:
– Convecção forçada: propriedades físicas
avaliadas na temperatura do escoamento externo.
• Assim, Re, Pr e Nu têm seus parâmetros avaliados por
Text (ou T∞).
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Convecção Natural x Forçada
• Para cada situação haverá uma correlação
específica para Nu.
• Deve-se tomar cuidado ao se determinar os
parâmetros de referência pois:
– Convecção natural: propriedades físicas
avaliadas na temperatura da película (filme), que
é uma média entre a T da parede e a externa:
Tf = (Tp+T∞)/2.
• Assim, β, Gr e Ra têm suas propriedades avaliadas por
Tf.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Regime laminar x turbulento
• Quem irá definir se o escoamento em uma
placa plana se encontra em uma ou outra
região será o número de Reynolds
(convecção forçada) ou o número de
Rayleigh (convecção natural):
– Para cada geometria há um valor de Reynolds e
de Rayleigh diferente para definir essa transição.
• Para cada regime, laminar ou turbulento,
haverá uma correlação específica para Nu.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Procedimento de cálculo – fluxo de calor
Determinar se o fluxo de calor ocorre por convecção
forçada ou natural e se o regime é laminar ou
turbulento (a partir de Re ou Ra)
Calcular Nu (Nu = h.L/k) usando as correlações
Determinar h (h = Nu.k/L)
•
•
Calcular fluxo calor por área (q”):
•
Calcular taxa de calor Q:
EM-524 Fenômenos de Transporte
q” = h.(Tp-T∞)
•
•
Q = q”.A
Profa. Dra. Carla K. N. Cavaliero
CONVECÇÃO FORÇADA – PLACA PLANA
propriedades avaliadas Text
local
Laminar
Rex<5.103
médio
T
Nux→Eq. 6.26
Q
Nux→Eq. 6.44
T
Nu→Eq. 6.30
Q
Nu→não há
Nu→Eq. 6.30
Transição
5.103<Rex<5.105
médio
T
Nu =
( Nu L )2
+ ( Nu T )
2
Nu→Eq. 6.37
T
local
Turbulento
5.105<Rex<107
Q
T
médio
EM-524 Fenômenos de Transporte
Q
Nux→Eq. 6.34
Nu→Eq. 6.37
Profa. Dra. Carla K. N. Cavaliero
CONVECÇÃO NATURAL – PLACA PLANA
propriedades avaliadas (TP+Text)/2
laminar
RaL< 109
RaL
Eq. 6.50
T
local
Nux→Eq. 6.51
médio
Nux→Eq. 6.52
local
turbulento
Nu→Eq. 6.54
médio
Vertical
laminar
Ra < 109
RaL*
Eq. 6.58
Q
Q/F
T
EM-524 Fenômenos de Transporte
Nux→Eq. 6.59
médio
Nux→Eq. 6.60
local
turbulento
Horizontal
local
F/Q
Nu→Eq. 6.61
médio
104<RaL<107
Nu→Eq. 6.55
107<RaL<1011
Nu→Eq. 6.56
105<RaL<1010
Nu→Eq. 6.57
Profa. Dra. Carla K. N. Cavaliero
CONVECÇÃO CILINDROS, TUBOS E ESFERAS
propriedades avaliadas Text
cilindros
ReLC<1
Convecção
Forçada
Isotérmica
0.6<Pr<1000
Nux→Eq. 6.46
Nux→Eq. 6.47
esferas
Nu→Eq. 6.30
1<ReLC<105
Nu = Nu 0 +
( Nu L )
2
+ ( Nu T )
2
Nu→Eq. 6.37
Eq. 6.45
Nu0&Lc→Tab. 6.5
Convecção
Natural
Isotérmica
Lam/Turb.
16

 Ra LC ⋅ ξ ⋅ Pr  
Nu =  Nu 0 + 
 
300

 

Eq. 6.63
EM-524 Fenômenos de Transporte
2
ξ→Eq. 6.64
Nu0 & Lc→Tab. 6.6
Profa. Dra. Carla K. N. Cavaliero
Exercícios - Capítulo 6
Escoamento externo: efeitos
viscosos e térmicos
Proposição de exercícios:
6.8/ 6.12/ 6.22/ 6.24/ 6.25/ 6.27/ 6.29/ 6.33/
6.34/ 6.35/ 6.38/ 6.39/ 6.40/ 6.42
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 1: Um arremessador em um jogo de beisebol é cronometrado
enquanto arremessa uma bola a 90 mph através do ar a 60o F. Se o
diâmetro da bola for de 2,80 in, calcule a força de arrasto sobre ela
supondo que os efeitos da rugosidade na superfície são desprezíveis.
Escoamento externo
Arrasto
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 1: Um arremessador em um jogo de beisebol é cronometrado
enquanto arremessa uma bola a 90 mph através do ar a 60o F. Se o
diâmetro da bola for de 2,80 in, calcule a força de arrasto sobre ela
supondo que os efeitos da rugosidade na superfície são desprezíveis.
d = 2,8 in = 7,11*10-2 m
U = 90 mph = 40,2 m/s
Propriedades do ar (60o F = 15,6o C): ν = 14,69*10-6 m2/s
ρ = 1,2229 kg/m3
A força de arrasto total será:
CD =
D
1
2
ρU Aesf
2
EM-524 Fenômenos de Transporte
1
2
⇒ D = C D ρU Aesf
2
Profa. Dra. Carla K. N. Cavaliero
Exercício 1: Um arremessador em um jogo de beisebol é cronometrado
enquanto arremessa uma bola a 90 mph através do ar a 60o F. Se o
diâmetro da bola for de 2,80 in, calcule a força de arrasto sobre ela
supondo que os efeitos da rugosidade na superfície são desprezíveis.
d = 2,8 in = 7,11*10-2 m
U = 90 mph = 40,2 m/s
Propriedades do ar (60o F = 15,6o C): ν = 14,69*10-6 m2/s
ρ = 1,2229 kg/m3
Re =
U *d
ν
40,2 * 7,11*10 −2
5
=
=
1
,
95
*
10
14,69 *10 −6
Fig : 6 − 15
C D = 0,4
2
−2
2
1
0
,
4
*
1
,
2229
*
(
40
,
2
)
*
4
π
(
7
,
11
*
10
/
2
)
D = C D ρU 2 Aesf =
= 6,27 N
2
2
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 2: Um lâmpada de 40W, de 10 cm de diâmetro, instalada
externamente está exposta ao ar que está a 14oC e na velocidade de
5m/s. Foi observado que a temperatura de sua superfície mantém-se
aproximadamente em 36oC. Estime a taxa de perda de calor por
convecção do bulbo considerando que a lâmpada seja esférica.
Tar = 14º C
Uar = 5 m/s
40W
d=10cm
Ts = 36º C
Escoamento externo
Convecção forçada
Temperatura da parede uniforme
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 2: Um lâmpada de 40W, de 10 cm de diâmetro, instalada
externamente está exposta ao ar que está a 14oC e na velocidade de
5m/s. Foi observado que a temperatura de sua superfície mantém-se
aproximadamente em 36oC. Estime a taxa de perda de calor por
convecção do bulbo considerando que a lâmpada seja esférica.
Tar = 14º C
Uar = 5 m/s
40W
d=10cm
Propriedades do ar a 14º C:
c p = 1005 J / kg oC
ρ = 1,246kg / m3
µ = 17,2.10 −6 kg / m.s k = 24,87.10 −3W / m oC
Ts = 36º C
ν = 13,31.10 −6 m 2 / s
Pr = 0,716
Q& = h A(T p − T∞ )
Re = ULc/ν = 5*0,1/13,31.10-6 = 3,8.104
Nu médio para uma esfera (1< ReLc < 105 &
Nu = Nu 0 +
EM-524 Fenômenos de Transporte
2
Nu lam
0.6 < Pr < 1000):
2
+ Nu tur
Profa. Dra. Carla K. N. Cavaliero
Exercício 2: Um lâmpada de 40W, de 10 cm de diâmetro, instalada
externamente está exposta ao ar que está a 14oC e na velocidade de
5m/s. Foi observado que a temperatura de sua superfície mantém-se
aproximadamente em 36oC. Estime a taxa de perda de calor por
convecção do bulbo considerando que a lâmpada seja esférica.
Tar = 14º C • Para esferas Nu = 2,0
o
Var = 5 m/s • Lc = d = 0,1m
40W
• Nu laminar:
d=10cm
c p = 1005 J / kg o C
N u L = 0,664(Re Lc )1/ 2 Pr1/ 3 = 115,8
Ts = 36º C
• Nu turbulento:
0 ,8
0,037 Re Lc Pr
N uT =
= 147
− 0 ,1
2/3
1 + 2,443 Re Lc (Pr − 1)
ρ = 1,246kg / m3
µ = 17,2.10−6 kg / m.s k = 24,87.10 −3W / m oC
ν = 13,31.10−6 m 2 / s
Pr = 0,716
Nu = Nu 0 + Nu
EM-524 Fenômenos de Transporte
2
lam
+ Nu
2
tur
= 189
Profa. Dra. Carla K. N. Cavaliero
Exercício 2: Um lâmpada de 40W, de 10 cm de diâmetro, instalada
externamente está exposta ao ar que está a 14oC e na velocidade de
5m/s. Foi observado que a temperatura de sua superfície mantém-se
aproximadamente em 36oC. Estime a taxa de perda de calor por
convecção do bulbo considerando que a lâmpada seja esférica.
Tar = 14º C
c p = 1005J / kg oC
Var = 5 m/s
µ = 17,2.10 −6 kg / m.s k = 24,87.10 −3W / m oC
ν = 13,31.10 −6 m 2 / s
40W
d=10cm
Ts = 36º C
ρ = 1,246kg / m 3
Pr = 0,716
• O coeficiente de calor médio
será:
N u.k 189 * 24,87.10 −3
h=
=
= 47 W/m 2oC
Lc
0,1
• E a taxa de perda de calor será:
Q& = h A(T p − T∞ ) = 47 * 4π (0,05) 2 * (36 − 14) = 32,5 W
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 3: Um condutor elétrico tem a forma de um cilindro com
diâmetro D = 25 mm e comprimento igual a 1 m. Ele é posicionado na
horizontal e a temperatura de sua superfície igual a 60oC, enquanto que
o ar que o circunda tem temperatura de 20oC. Determine a potência em
W dissipada pelo condutor no ambiente. Utilize a relação proposta onde
a dimensão característica L é o próprio diâmetro D.
Escoamento externo
Convecção natural
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 3: Um condutor elétrico tem a forma de um cilindro com
diâmetro D = 25 mm e comprimento igual a 1 m. Ele é posicionado na
horizontal e a temperatura de sua superfície igual a 60oC, enquanto que
o ar que o circunda tem temperatura de 20oC. Determine a potência em
W dissipada pelo condutor no ambiente. Utilize a relação proposta onde
a dimensão característica L é o próprio diâmetro D.

0,387 Ra D
N u D = 0,60 +

1 + (0,559 / Pr) 9 /16
ρ 2 c p gβ (T p − Tar ) D 3
RaD =
µ .k
1/ 6
(

8 / 27 

2
)
• Tf = (Tp+T∞)/2= 40ºC
• Propriedades do ar a 40º C: cp=1006,8 J/kg.ºC;
ρ=1,1273 kg/m3; ν=1,70.10-5 m2/s; k=2,71.10-2 W/mºC;
Pr=0,71; β=1/Tf =0,0032 K
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 3: Um condutor elétrico tem a forma de um cilindro com
diâmetro D = 25 mm e comprimento igual a 1 m. Ele é posicionado na
horizontal, a temperatura de sua superfície igual a 60oC enquanto que o
ar que o circunda tem temperatura de 20oC. Determine a potência em
W dissipada pelo condutor no ambiente. Utilize a relação proposta onde
a dimensão característica L é o próprio diâmetro D.
ρ 2 c p gβ (Tp − Tar ) D 3
Ra D =
= 4,85.10 4
µ .k

0,387 RaD
N u D = 0,60 +

1 + (0,559 / Pr)9 / 16
1/ 6
(
2

= 6,5
8 / 27 

)
N u D .k
h=
= 7 W/m 2oC
D
Q& = h A(Tp − T∞ ) = h PL(Tp − T∞ ) = 7 * π * 0,025 * 1* (60 − 20) = 22 W
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 4: Uma piscina externa aquecida (15 m de largura e 30 m de
comprimento) em uma estação de esqui é coberta durante a noite para
reduzir a perda de calor. Numa noite típica de inverno, a temperatura
do ar está a -10 ºC e o vento sopra à velocidade de 3 m/s sobre a piscina
na direção de seu comprimento. Considerando que a temperatura da
cobertura da piscina em contato com o ar é de 25 ºC, estime a taxa
média de energia (kW) transferida para manter a temperatura da
piscina constante. Suponha que os lados e o fundo da piscina estejam
bem isolados.
Escoamento Externo
Convecção forçada
Temperatura da parede
uniforme
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 4: Uma piscina externa aquecida (15 m de largura e 30 m de
comprimento) em uma estação de esqui é coberta durante a noite para
reduzir a perda de calor. Numa noite típica de inverno, a temperatura
do ar está a -10 ºC e o vento sopra à velocidade de 3 m/s sobre a piscina
na direção de seu comprimento. Considerando que a temperatura da
cobertura da piscina em contato com o ar é de 25 ºC, estime a taxa
média de energia (kW) transferida para manter a temperatura da
piscina constante. Suponha que os lados e o fundo da piscina estejam
bem isolados.
Q& = h . A.(Tp − T∞ )
Piscina: 15 m largura x 30 m comprimento
Propriedades do ar -10º C:
T∞ = -10º C
Tp = 25º C
U = 3 m/s
EM-524 Fenômenos de Transporte
cp = 1,0056 kJ/kg.ºC
ρ = 1,3414 kg/m3
µ = 16,71.10-6 kg/m.s
ν = 12,46.10-6 m2/s
k = 23,29.10-3 W/m.ºC
Pr = 0,721
Profa. Dra. Carla K. N. Cavaliero
Exercício 4: Uma piscina externa aquecida (15 m de largura e 30 m de
comprimento) em uma estação de esqui é coberta durante a noite para
reduzir a perda de calor. Numa noite típica de inverno, a temperatura
do ar está a -10 ºC e o vento sopra à velocidade de 3 m/s sobre a piscina
na direção de seu comprimento. Considerando que a temperatura da
cobertura da piscina em contato com o ar é de 25 ºC, estime a taxa
média de energia (kW) transferida para manter a temperatura da
piscina constante. Suponha que os lados e o fundo da piscina estejam
bem isolados.
ρUL UL
3 * 30
6
Re =
=
=
=
7
,
223
.
10
µ
ν 12,46.10 −6
O escoamento é turbulento
(Re > 5.105)
0,037 Re0,8 Pr
N uT =
1 + 2,443 Re− 0 ,1 (Pr 2 / 3 − 1)
0,037(7,223.106 )0,8 * 0,721
3
N uT =
=
9
,
083
.
10
1 + 2,443(7,223.106 )− 0 ,1 ( 0,7212 / 3 − 1)
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Exercício 4: Uma piscina externa aquecida (15 m de largura e 30 m de
comprimento) em uma estação de esqui é coberta durante a noite para
reduzir a perda de calor. Numa noite típica de inverno, a temperatura
do ar está a -10 ºC e o vento sopra à velocidade de 3 m/s sobre a piscina
na direção de seu comprimento. Considerando que a temperatura da
cobertura da piscina em contato com o ar é de 25 ºC, estime a taxa
média de energia (kW) transferida para manter a temperatura da
piscina constante. Suponha que os lados e o fundo da piscina estejam
bem isolados.
hL
N u.k 9,083.103 * 23,29.10 −3
Nu =
⇒h =
=
= 7,05W / m 2 oC
k
L
30
Q& = h. A.(Tp − T∞ ) = 7,05 * (15 * 30)(25 − (−10)) = 1,11.105W = 111kW
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
Existem tópicos do Cap. 6 que não
foram revisados para a execução dos
exercícios anteriores.
Eles precisarão ser estudados para a
resolução dos exercícios
recomendados do livro.
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero
FIM !
EM-524 Fenômenos de Transporte
Profa. Dra. Carla K. N. Cavaliero